傅里叶变换五大主要特性介绍
我们来深入解读傅里叶变换的五大主要特性。这五大特性不仅是傅里叶变换理论的核心支柱，也是其在工程、物理和数学领域得以广泛应用的根本原因。
理解这些特性，能让我们从“会计算”提升到“懂本质”的层面。
首先，我们统一一下符号：
时域信号为 x(t)，其对应的傅里叶变换为X(f) 或 X(ω)。
傅里叶变换对表示为：
一、线性性
线性性是最直观也最基本的特性。它描述了两个或多个信号在时域中叠加（相加和缩放）后，其频域表示也会发生相应的叠加。
数学表达
若
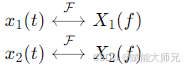
则对于任意常数 a 和 b，有：
时域信号的幅度放大，对应于频域信号幅度的放大。
物理意义：现实世界中的复杂信号往往是由多个简单信号组合而成的。例如，一段音乐是由不同频率、不同强度的正弦波（乐器声音）叠加而成。线性性保证了我们可以先分析每个单一成分的频谱，然后简单地相加，就能得到整个复杂信号的频谱。
系统分析：在线性时不变系统中，如果输入信号可以分解为多个基本信号的叠加，那么系统的总输出就是这些基本信号各自响应的叠加。傅里叶变换的线性性为此提供了完美的数学工具。
基础地位：这是所有线性变换（如拉普拉斯变换、Z变换）共有的根本属性，是信号与系统分析能够进行“分解与合成”的前提。
二、时移特性
时移特性描述了当一个信号在时间轴上发生延迟或提前（即平移）时，其频域表示会发生怎样的变化。
数学表达
若
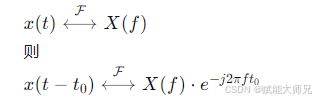
幅度不变，相位变化：这是该特性的核心结论。信号在时间上的平移不会改变其幅度谱 ∣X(f)∣，而只会改变其相位谱 ∠X(f)。
- 新的相位谱为：
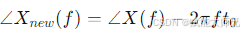
物理意义：无论你是在上午8点还是9点开始播放同一首歌曲，这首歌所包含的频率成分（音高）和强度（响度）是完全一样的，改变的只是它开始的时间。时移特性精确地刻画了这一事实。
工程应用：
- 雷达与声纳：通过比较发送信号和接收回波信号的相位差，可以精确计算出目标的距离。因为延迟时间 t0 就蕴含在相位变化
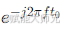中。 - 通信同步：在接收端需要找到信号的起始位置（帧同步），时移特性帮助工程师理解时间偏差对接收信号相位的影响。
三、频移特性
频移特性是时移特性的对偶特性。它描述了将一个信号与一个复指数信号（或正弦/余弦信号）相乘时，其频谱在频率轴上会发生平移。
数学表达
若
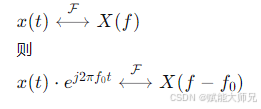
频谱搬移：这是该特性的核心作用。一个信号的频谱X(f) 会被整体搬移到以 f0 为中心的位置。
物理意义与核心应用：调制
振幅调制：这是通信系统的基石。我们想要传输的语音或数据信号 x(t)（频谱在低频，称为基带信号）无法直接在空间中有效传播。我们需要将其“装载”到一个高频载波 cos(2πf0t) 上。
由于
，根据线性性和频移特性，调制后的信号x(t)cos(2πf0t)的频谱将是 
。即将基带频谱搬移到了载波频率 ±f0 的两侧，从而能够通过天线发射。
解调是调制的逆过程，同样利用频移特性将频谱搬回基带。
超外差接收机、混频器等现代无线电设备都基于此原理。
四、卷积定理
卷积定理是傅里叶变换中最强大、最实用的特性之一。它建立了时域中复杂的卷积运算与频域中简单的乘法运算之间的等价关系。
数学表达
系统分析的革命：在时域中，计算一个LTI系统对输入信号 x(t) 的响应 y(t) 需要进行卷积运算：y(t)=x(t)∗h(t)。卷积运算通常非常复杂和耗时。
计算简化：卷积定理告诉我们，可以转而计算：
- 求 X(f)=F{x(t)}
- 求 H(f)=F{h(t)}（系统传递函数）
- 在频域相乘：Y(f)=X(f)⋅H(f)
- 再反变换回时域：
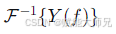
- 由于乘法运算远比卷积运算简单，尤其是在数字信号处理中，这极大地降低了计算复杂度。
滤波器的设计与应用：
- 滤波的本质就是通过乘法来塑造频谱。我们希望得到一个理想的滤波器 H(f)，它在通带内为1，阻带内为0。将输入信号的频谱 X(f) 与此滤波器频谱相乘 Y(f)=X(f)⋅H(f)，就能轻松地保留某些频率成分，去除另一些成分。
- 根据卷积定理，这个频域的乘法操作，等效于在时域进行卷积。而时域的卷积核就是滤波器单位冲激响应 h(t) 的反傅里叶变换。
对偶性：该定理完美体现了时域与频域之间的对偶关系：时域的复杂运算对应频域的简单运算，反之亦然。
五、帕塞瓦尔定理
帕塞瓦尔定理揭示了信号在时域和频域之间的能量守恒关系。信号的总能量既可以在时域通过积分计算，也可以在频域通过对其频谱幅度的平方进行积分来计算。
数学表达
对于能量信号 x(t)：
能量守恒：该定理表明，傅里叶变换是一种“能量守恒”的变换。信号的能量不会因为我们从时域视角切换到频域视角而消失或增加，它只是被重新分配和描述了。
物理意义：等式左边 
表示信号在全部时间上的总能量。等式右边
可以理解为将总能量按频率进行分解。被积函数
称为信号的能量谱密度，它描述了信号能量在频率轴上的分布情况。
核心应用：
- 信号分析与比较：我们可以通过比较能量谱密度来确定信号的主要能量集中在哪些频带，这对于带宽估计、信号识别至关重要。
- 滤波器性能评估：一个滤波器滤除了多少噪声能量？通过计算输入和输出信号的能量谱，可以精确量化滤波器的效果。
- 功率估计：在通信系统中，用于计算信号功率和信噪比。
- 物理学的桥梁：在量子力学中，波函数的模方表示概率密度，帕塞瓦尔定理则保证了坐标空间和动量空间中的概率总和是一致的。
六、总结
这五大特性构成了一个完整的框架，让我们能够自由地在时域和频域之间穿梭，并用最便捷的方式解决实际问题：
线性性是基础，允许我们分解和合成信号。
时移/频移特性揭示了时空与频率的对称与关联，是调制、同步和测距的理论核心。
卷积定理是连接系统输入、输出和系统本身的桥梁，是信号处理算法的效率之源。
帕塞瓦尔定理是保证，它告诉我们变换过程中的能量是守恒的，使得频域分析在物理上是真实可靠的。
掌握这五大特性，就等于掌握了傅里叶变换的精髓。