线性代数 - 特征值和特征向量可视化是什么样的
线性代数 - 特征值和特征向量可视化是什么样的
flyfish
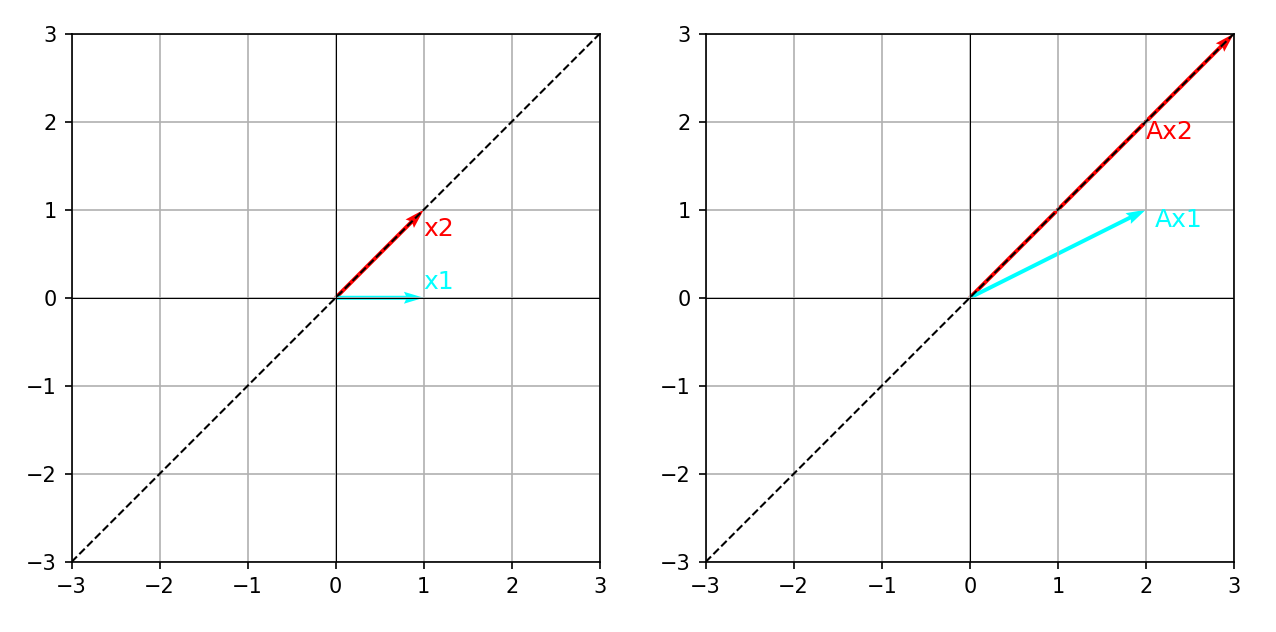
特征值和特征向量
在线性代数中,假设有一个矩阵 AAA 表示一个线性变换。对于一个非零向量 x\mathbf{x}x,如果应用这个变换后得到的结果 AxA \mathbf{x}Ax 与原向量 x\mathbf{x}x 是平行关系(即只发生缩放,而不改变方向),那么 x\mathbf{x}x 就称为矩阵 AAA 的特征向量(eigenvector)。数学上,这满足方程:
Ax=λxA \mathbf{x} = \lambda \mathbf{x}Ax=λx
其中,λ\lambdaλ 是缩放因子,称为对应的特征值(eigenvalue)。特征值可以是正数(表示放大)、负数(表示放大并反转方向)或零(表示向量被映射到零向量)。
在上图中:
向量 x1\mathbf{x_1}x1(蓝色)经过变换 AAA 后,成为 Ax1A \mathbf{x_1}Ax1,但不再与原向量在同一条直线上(方向改变了),所以 x1\mathbf{x_1}x1 不是特征向量。
向量 x2\mathbf{x_2}x2(红色)经过变换 AAA 后,成为 Ax2=λx2A \mathbf{x_2} = \lambda \mathbf{x_2}Ax2=λx2,仍然在同一条直线上(只发生了缩放),所以 x2\mathbf{x_2}x2 是特征向量,λ\lambdaλ 是特征值。
代码实现
import matplotlib.pyplot as plt
import numpy as np# 定义矩阵 A
A = np.array([[2, 1], [1, 2]])# 定义向量 x1(非特征向量)和 x2(特征向量)
x1 = np.array([1, 0]) # 蓝色
x2 = np.array([1, 1]) # 红色# 计算变换后的向量
Ax1 = A @ x1
Ax2 = A @ x2# 创建画布和子图
fig, axs = plt.subplots(1, 2, figsize=(10, 5))# 左子图:原始向量 x1 和 x2
axs[0].quiver(0, 0, x2[0], x2[1], angles='xy', scale_units='xy', scale=1, color='red')
axs[0].quiver(0, 0, x1[0], x1[1], angles='xy', scale_units='xy', scale=1, color='cyan')
axs[0].set_xlim(-3, 3)
axs[0].set_ylim(-3, 3)
axs[0].axhline(0, color='black', linewidth=0.5)
axs[0].axvline(0, color='black', linewidth=0.5)
# 添加虚线表示 y = x 直线
axs[0].plot([-3, 3], [-3, 3], 'k--', linewidth=1) # 黑色虚线
axs[0].grid(True)
axs[0].set_aspect('equal')axs[0].text(x2[0]*0.5 + 0.5, x2[1]*0.5 + 0.2, 'x2', color='red', fontsize=12)
axs[0].text(x1[0]*0.5 + 0.5, x1[1]*0.5 + 0.1, 'x1', color='cyan', fontsize=12)# 添加箭头表示变换 A
axs[0].annotate('', xy=(5, 0), xytext=(4.5, 0), arrowprops=dict(facecolor='black', shrink=0.05))
axs[0].text(4.6, 0.1, 'A', fontsize=14)# 右子图:变换后的向量 Ax1 和 Ax2
axs[1].quiver(0, 0, Ax2[0], Ax2[1], angles='xy', scale_units='xy', scale=1, color='red')
axs[1].quiver(0, 0, Ax1[0], Ax1[1], angles='xy', scale_units='xy', scale=1, color='cyan')
axs[1].set_xlim(-3, 3)
axs[1].set_ylim(-3, 3)
axs[1].axhline(0, color='black', linewidth=0.5)
axs[1].axvline(0, color='black', linewidth=0.5)
# 添加虚线表示 y = x 直线
axs[1].plot([-3, 3], [-3, 3], 'k--', linewidth=1) # 黑色虚线
axs[1].grid(True)
axs[1].set_aspect('equal')axs[1].text(Ax2[0]*0.5 + 0.5, Ax2[1]*0.5 + 0.3, 'Ax2', color='red', fontsize=12)
axs[1].text(Ax1[0]*0.5 + 1.1, Ax1[1]*0.5 + 0.3, 'Ax1', color='cyan', fontsize=12)# 保存为 JPG 文件
plt.savefig('eigenvectors_diagram.jpg', dpi=300, bbox_inches='tight')
plt.show()
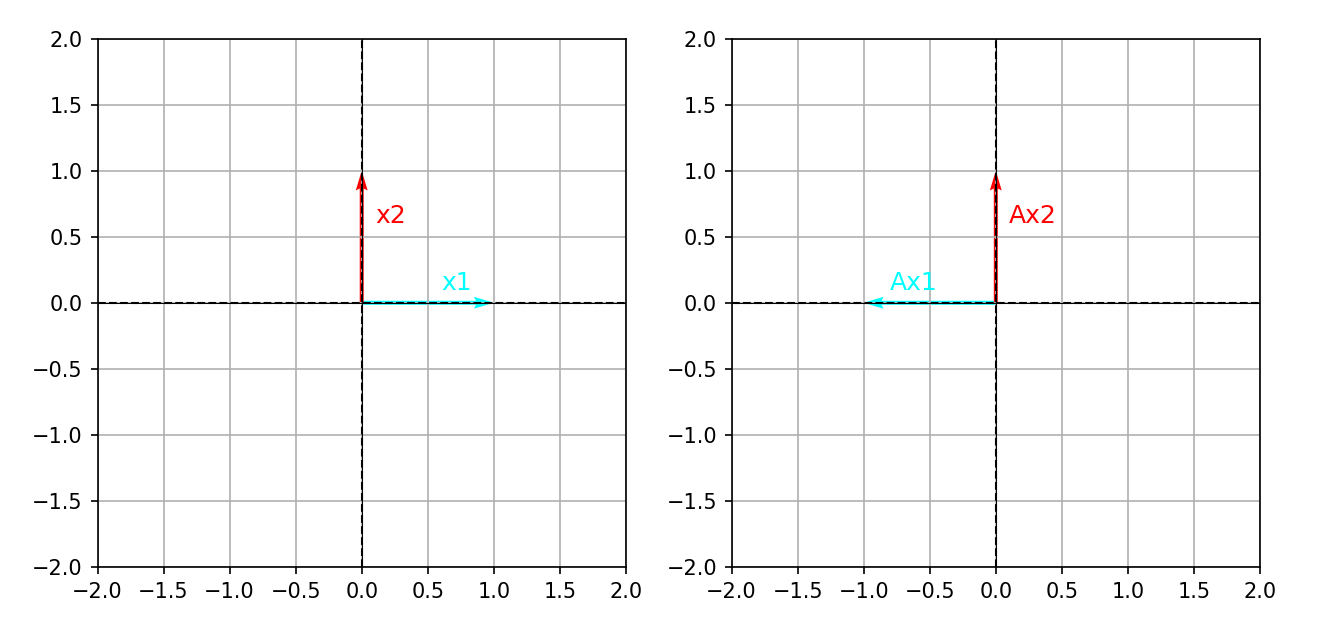
关于y轴的反射矩阵A=(−1001)A = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}A=(−1001),
y轴方向的向量 x⃗=(01)\vec{x} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}x=(01) 变换后仍为 (01)\begin{pmatrix} 0 \\ 1 \end{pmatrix}(01)(伸缩比例λ=1\lambda=1λ=1);
x轴方向的向量 x⃗=(10)\vec{x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}x=(10) 变换后为 (−10)\begin{pmatrix} -1 \\ 0 \end{pmatrix}(−10)(伸缩比例λ=−1\lambda=-1λ=−1,反向伸缩)。
定义 Ax⃗=λx⃗A\vec{x} = \lambda \vec{x}Ax=λx 就是为了精准捕捉这类“方向不变、仅伸缩”的特殊向量(特征向量x⃗\vec{x}x)和伸缩比例(特征值λ\lambdaλ)。
import matplotlib.pyplot as plt
import numpy as np# 定义矩阵 A:关于y轴的反射矩阵
A = np.array([[-1, 0], [0, 1]])# 定义向量 x1(x轴方向)和 x2(y轴方向)
x1 = np.array([1, 0]) # 蓝色,特征向量,λ=-1
x2 = np.array([0, 1]) # 红色,特征向量,λ=1# 计算变换后的向量
Ax1 = A @ x1 # [-1, 0]
Ax2 = A @ x2 # [0, 1]# 创建画布和子图
fig, axs = plt.subplots(1, 2, figsize=(10, 5))# 左子图:原始向量 x1 和 x2
axs[0].quiver(0, 0, x1[0], x1[1], angles='xy', scale_units='xy', scale=1, color='cyan')
axs[0].quiver(0, 0, x2[0], x2[1], angles='xy', scale_units='xy', scale=1, color='red')
axs[0].set_xlim(-2, 2)
axs[0].set_ylim(-2, 2)
axs[0].axhline(0, color='black', linewidth=0.5)
axs[0].axvline(0, color='black', linewidth=0.5)
# 添加虚线表示 x轴和 y轴(作为参考,直线表示方向不变)
axs[0].plot([-2, 2], [0, 0], 'k--', linewidth=1) # x轴虚线
axs[0].plot([0, 0], [-2, 2], 'k--', linewidth=1) # y轴虚线
axs[0].grid(True)
axs[0].set_aspect('equal')axs[0].text(x1[0]*0.5 + 0.1, x1[1]*0.5 + 0.1, 'x1', color='cyan', fontsize=12)
axs[0].text(x2[0]*0.5 + 0.1, x2[1]*0.5 + 0.1, 'x2', color='red', fontsize=12)# 添加箭头表示变换 A
axs[0].annotate('', xy=(5, 0), xytext=(4.5, 0), arrowprops=dict(facecolor='black', shrink=0.05))
axs[0].text(4.6, 0.1, 'A', fontsize=14)# 右子图:变换后的向量 Ax1 和 Ax2
axs[1].quiver(0, 0, Ax1[0], Ax1[1], angles='xy', scale_units='xy', scale=1, color='cyan')
axs[1].quiver(0, 0, Ax2[0], Ax2[1], angles='xy', scale_units='xy', scale=1, color='red')
axs[1].set_xlim(-2, 2)
axs[1].set_ylim(-2, 2)
axs[1].axhline(0, color='black', linewidth=0.5)
axs[1].axvline(0, color='black', linewidth=0.5)
# 添加虚线表示 x轴和 y轴
axs[1].plot([-2, 2], [0, 0], 'k--', linewidth=1) # x轴虚线
axs[1].plot([0, 0], [-2, 2], 'k--', linewidth=1) # y轴虚线
axs[1].grid(True)
axs[1].set_aspect('equal')axs[1].text(Ax1[0]*0.5 - 0.3, Ax1[1]*0.5 + 0.1, 'Ax1', color='cyan', fontsize=12) # Ax1 为负方向,调整位置
axs[1].text(Ax2[0]*0.5 + 0.1, Ax2[1]*0.5 + 0.1, 'Ax2', color='red', fontsize=12)# 保存为 JPG 文件
plt.savefig('reflection_matrix_visualization.jpg', dpi=300, bbox_inches='tight')
plt.show() #
反射矩阵(也称为镜射矩阵)在线性代数中,是一个表示向量在某个超平面(如直线或平面)上进行镜面反射的线性变换矩阵。这种变换是一种正交变换,保持向量的长度不变,但会翻转其在反射平面上的分量。简单来说,它像一面镜子,将空间的一侧“反射”到另一侧。
假设在二维欧氏空间中,对于一个向量 v⃗=(xy)\vec{v} = \begin{pmatrix} x \\ y \end{pmatrix}v=(xy),反射矩阵 AAA 满足 Av⃗=v⃗′A \vec{v} = \vec{v}'Av=v′,其中 v⃗′\vec{v}'v′ 是 v⃗\vec{v}v 关于反射轴的镜像。反射矩阵的通用形式依赖于反射平面。对于标准轴:
关于y轴的反射:A=(−1001)A = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}A=(−1001)。例如,点(1, 2)反射后变为(-1, 2)。
关于x轴的反射:A=(100−1)A = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}A=(100−1)。点(1, 2)反射后变为(1, -2)。
关于直线y = x的反射:A=(0110)A = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}A=(0110)。点(1, 2)反射后变为(2, 1)。
