机器学习(4) cost function(代价函数)
目录
- 介绍
介绍
-
书接上文,现在我们的模型是 f w , b x = w x + b f_{w,b}x=wx+b fw,bx=wx+b,其中, w , b w,b w,b是模型参数,也被称为系数或者权重。那么我们有以下的结论
y ^ ( i ) = f w , b x ( i ) = w x ( i ) + b \hat{y}^{(i)}=f_{w,b}x^{(i)}=wx^{(i)}+b y^(i)=fw,bx(i)=wx(i)+b
现在我们的目标是找到合适的模型参数 w w w和 b b b,使得对于所有的 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)), y ^ ( i ) \hat{y}^{(i)} y^(i)尽可能接近 y ( i ) y^{(i)} y(i) -
为了在整个数据集上计算误差,定义下面的函数为 c o s t f u n c t i o n cost\ function cost function,为了让这个值不会随着训练集大小增加而变大,计算平均平方误差,其中 m m m为样本数量,除以2是为了方便求导
J ( w , b ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 J(w,b) =\frac{1}{2m}\sum_{i=1}^{m}(\hat y^{(i)}-y^{(i)})^2 J(w,b)=2m1i=1∑m(y^(i)−y(i))2 -
举个简单的例子,假设实际的点坐标为 ( 1 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) (1,1),(2,2),(3,3) (1,1),(2,2),(3,3), c o s t f u n c t i o n cost\ function cost function参数为 w = 0.5 , b = 0 w=0.5,b=0 w=0.5,b=0,有 f ( x ) = 0.5 x f(x)=0.5x f(x)=0.5x,样本数 m = 3 m=3 m=3,图像如下
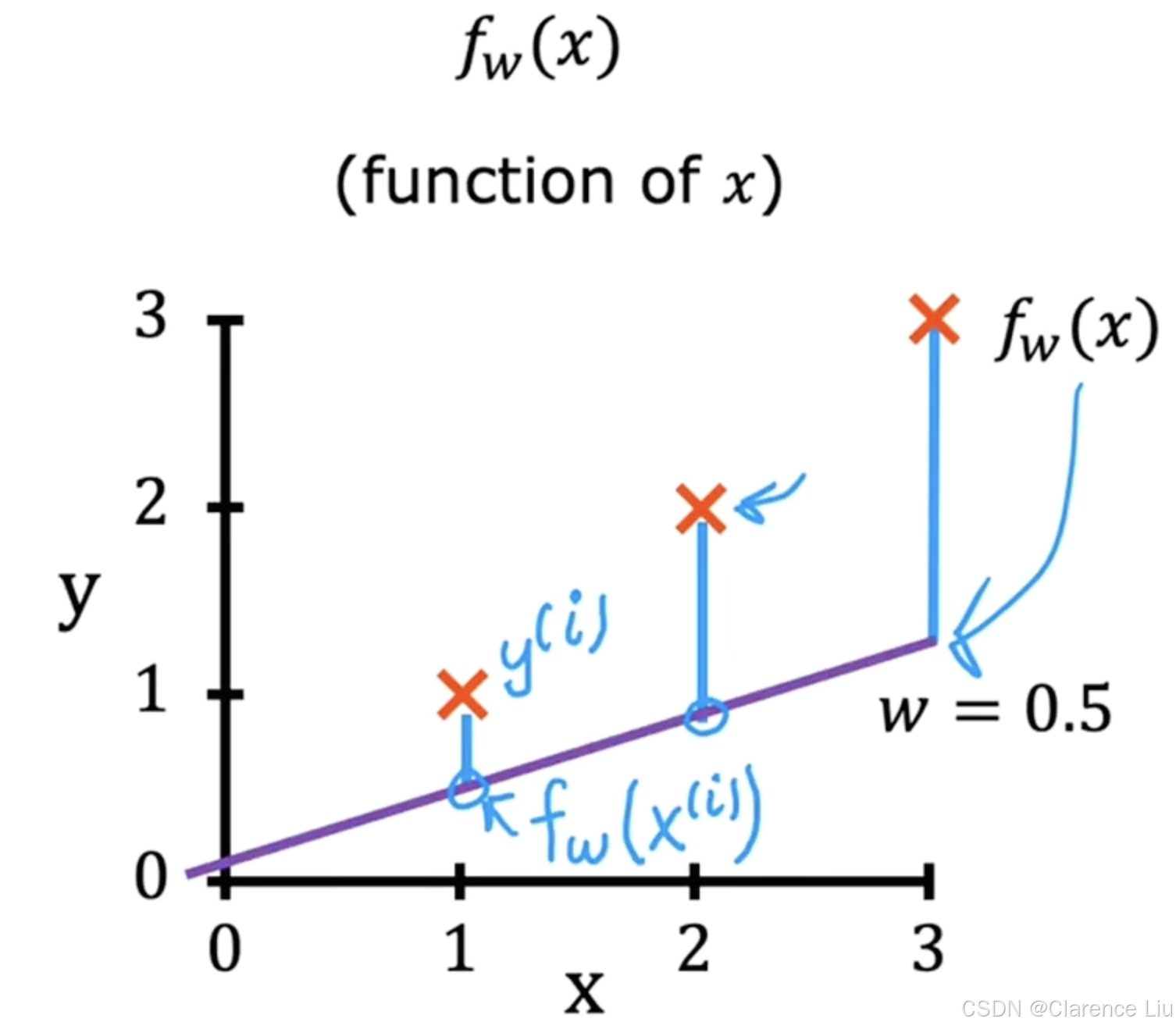
-
那么有
J ( w , b ) = 1 2 × 3 [ ( 0.5 − 1 ) 2 + ( 1 − 2 ) 2 + ( 1.5 − 3 ) 2 ] ≈ 0.58 J(w,b)=\frac{{1}}{{2\times3}}[(0.5-1)^2+(1-2)^2+(1.5-3)^2]\approx0.58 J(w,b)=2×31[(0.5−1)2+(1−2)2+(1.5−3)2]≈0.58
这就是所谓的 c o s t f u n c t i o n cost\ function cost function,线性回归的目标就是找到最合适的 ( w , b ) (w,b) (w,b),使得 J ( w , b ) J(w,b) J(w,b)尽可能地小。对于每一个 ( w , b ) (w,b) (w,b),针对数据集进行训练,会得到下面这样一个等高线图
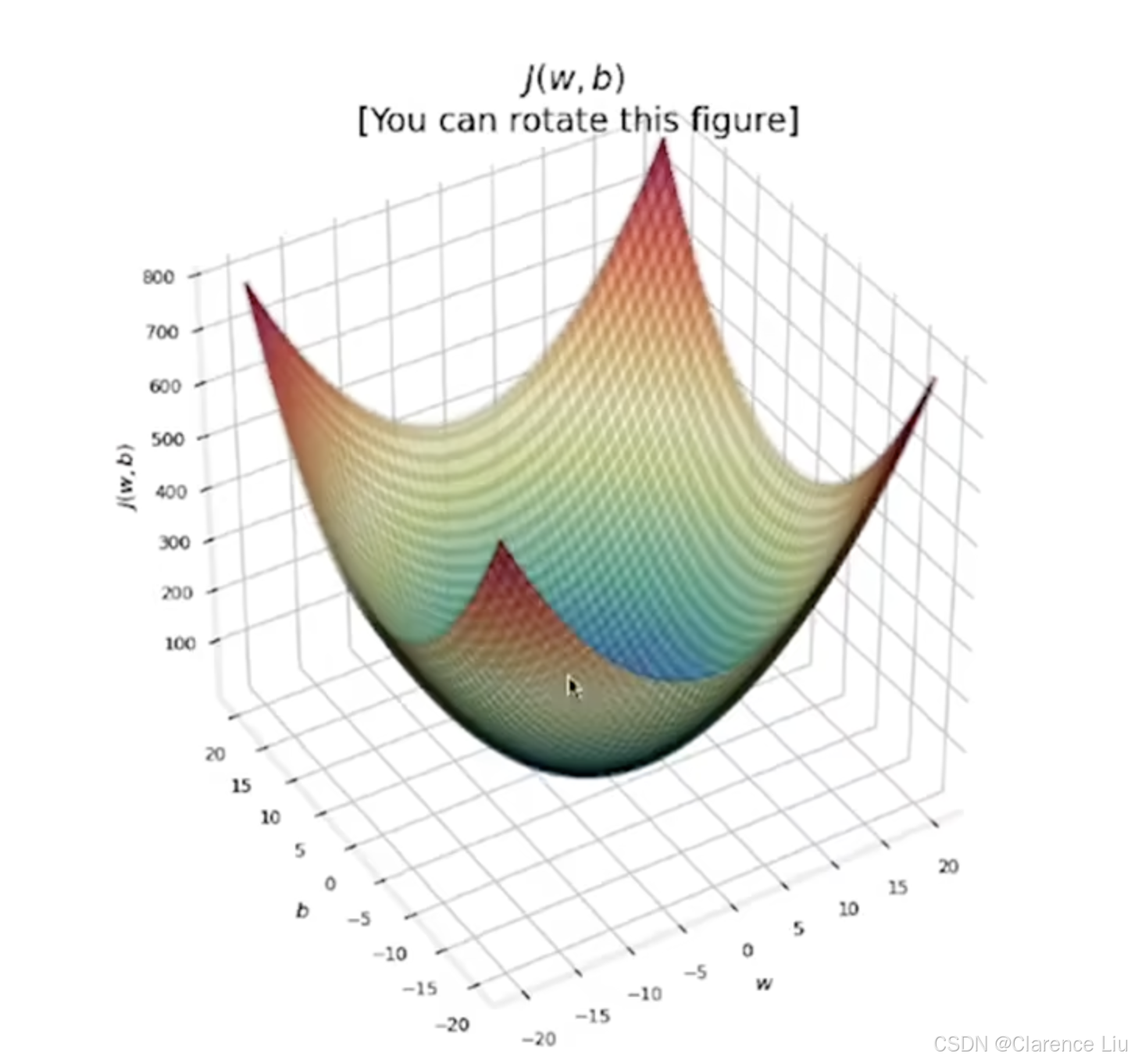
-
梯度下降( g r a d i e n t d e s c e n t gradient\ descent gradient descent)算法就是一个找到等高线图最低点的算法,也就是找到使得 c o s t f u n c t i o n cost\ function cost function最小的参数 w w w和 b b b。这个算法在机器学习领域被广泛运用,我么将在下节学习这个算法
