当前位置：首页 > news >正文

霍夫变换和基于时频脊线的汽车FMCW雷达干扰抑制——论文阅读

news 2025/11/10 8:53:42

霍夫变换和基于时频脊线的汽车FMCW雷达干扰抑制

A. Gaur, S. Srirangarajan, P. -H. Tseng and K. -T. Feng, “Hough Transform and Time-Frequency Ridge-Based Interference Mitigation in Automotive FMCW Radars,” 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, Singapore, 2024, pp. 1-7

随着FMCW雷达成为自动驾驶技术（ADAS）的关键组成部分，工作在76-81 GHz频段的雷达数量激增，导致雷达之间的相互干扰已成为一个亟待解决的重大挑战。这种干扰会提高噪声基底，导致漏检弱目标或误检“鬼影”目标，严重威胁行车安全。

现有的干扰管理方法主要分为两类：

信号与系统设计：通过设计新的发射波形、天线阵列或基于通信的协调方案来避免干扰，但这通常需要修改硬件或增加系统复杂性。
信号处理：在接收端通过算法减轻干扰，无需改动硬件。

本文提出了一种新颖的、基于信号处理的框架，称为HTFR（Hough Transform and Time-Frequency Ridge）。

其核心思想是：在时频（T-F）域中，目标回波和干扰信号都表现为线条，但具有截然不同的斜率特性。

目标回波：在接收端混频后，表现为单音频率，在T-F谱上是平行于时间轴的水平线。
干扰信号：由于干扰雷达的啁啾斜率与本车雷达不同，混频后仍表现为啁啾信号（Chirp），在T-F谱上是有斜率的线。

HTFR算法利用这一显著差异，将T-F谱视为一幅图像，通过图像处理技术来智能地分离和减轻干扰。

信号模型与问题构建

理解该方法的前提是建立FMCW雷达的信号模型。

假设“受害”雷达发射的单个归一化啁啾信号 $x (t)$ 其相位是时间的二次函数：
$x(t)=exp⁡[j2π(fot+12μt2)]x(t)=\exp[j2\pi(f_{o}t+\frac{1}{2}\mu t^{2})]$
其中 $f_o$ 是载波频率， $μ\mu$ 是啁啾斜率（ $μ=B/T\mu = B/T$ ，B是带宽，T是周期）。

1. 目标回波信号
来自 $M$ 个目标的回波信号 $x_r(t)$ 是发射信号的多个时延版本的叠加。对于第 $m$ 个目标：
$xr(t)=∑m=1Mαmexp⁡[j2π(fo(t−τm)+12μ(t−τm)2)]x_{r}(t)=\sum_{m=1}^{M}\alpha_{m}\exp[j2\pi(f_{o}(t-\tau_{m})+\frac{1}{2}\mu(t-\tau_{m})^{2})]$
其中 $αm\alpha_m$ 是复振幅， $τm\tau_m$ 是传播延迟， $τm=2(Rm+Vmt)c\tau_{m} = \frac{2(R_{m}+V_{m}t)}{c}$ ，它同时包含了目标的距离 $R_m$ 和速度 $V_m$ 。

2. 干扰信号
假设存在 $Q$ 个干扰雷达，它们组合的干扰信号 $x_{int}(t)$ 为：
$xint(t)=∑q=1Qαqexp⁡[j2π(fq(t−τq′)+12βq(t−τq′)2)]x_{int}(t)=\sum_{q=1}^{Q}\alpha_{q}\exp[j2\pi(f_{q}(t-\tau_{q}^{\prime})+\frac{1}{2}\beta_{q}(t-\tau_{q}^{\prime})^{2})]$
这些干扰雷达具有不同的载频 $f_q$ 和（关键）不同的啁啾斜率 $βq\beta_q$ 。

3. 拍频信号 (Beat Signal)
在雷达接收端，总信号 $r(t) = x_r(t) + x_{int}(t)$ 。接收机将其与发射信号的共轭 $x^*(t)$ 进行混频（解啁啾），得到拍频信号 $r_b(t)$ ：
$rb(t)=[xr(t)+xint(t)]⋅x∗(t)=xb(t)+xb,int(t)r_{b}(t)=[x_{r}(t)+x_{int}(t)]\cdot x^{*}(t) = x_{b}(t)+x_{b,int}(t)$

经过混频后，目标拍频信号 $x_b(t)$ （在忽略极小的 $τm2\tau_m^2$ 项后）简化为：
$xb(t)≈∑m=1Mαm′exp⁡[j2π(−foτm−μtτm)]x_{b}(t) \approx \sum_{m=1}^{M}\alpha_{m}^{\prime}\exp[j2\pi(-f_{o}\tau_{m}-\mu t\tau_{m})]$

这是一个关键结果：目标信号 $x_b(t)$ 是一组正弦信号（单音）的叠加。其频率 $fb=−μτmf_b = -\mu\tau_m$ ，是一个常数（或随 $t$ 缓慢变化，但仍是“线”），因此在T-F谱上表现为水平线。

而干扰拍频信号 $x_{b,int}(t)$ 则变为：
$xb,int(t)=∑q=1Qαq′exp⁡[j2π((fq−fo)t+12(βq−μ)t2)]x_{b,int}(t)=\sum_{q=1}^{Q}\alpha_{q}^{\prime}\exp[j2\pi((f_{q}-f_{o})t+\frac{1}{2}(\beta_{q}-\mu)t^{2})]$

这是另一个关键结果：由于干扰斜率 $βq\beta_q$ 与本车斜率 $μ\mu$ 不同 ( $βq≠μ\beta_q \ne \mu$ )，二次项 $12(βq−μ)t2\frac{1}{2}(\beta_{q}-\mu)t^{2}$ 不会被消除。

这意味着干扰信号 $x_{b,int}(t)$ 仍然是一个啁啾信号，其瞬时频率 $finst(t)=(fq−fo)+(βq−μ)tf_{inst}(t) = (f_q-f_o) + (\beta_q-\mu)t$ 是随时间 $t$ 线性变化的，因此在T-F谱上表现为倾斜的线。

最终，信号经过一个截止频率为 $f_{b,max}$ 的低通滤波器 $h (t)$ ，并混入加性高斯白噪声 $η(t)\eta(t)$ ，得到最终的接收信号 $r~b(t)\tilde{r}_{b}(t)$ ：
$τ~b(t)=xb(t)∗h(t)+xb,int(t)∗h(t)+η(t)\tilde{\tau}_{b}(t)=x_{b}(t)*h(t) + x_{b,int}(t)*h(t) + \eta(t)$
本文的目标就是从 $r~b(t)\tilde{r}_{b}(t)$ 中高效地分离出 $x_b(t)$ 。

提出的 HTFR 算法流程

该算法（Algorithm 1）分为三个主要步骤，将信号处理与图像处理技术相结合。

A. 时频分析 (FSST)

算法的第一步是获取受污染信号 $r~b(t)\tilde{r}_{b}(t)$ 的高分辨率时频（T-F）谱。本文没有使用传统的短时傅里叶变换（STFT），而是采用了傅里叶同步压缩变换（FSST）。

FSST的优势在于其“聚焦”特性。STFT会将能量分散在时间和频率上（模糊），而FSST通过“重排”STFT的系数，能将正弦波（即我们的目标信号）在T-F谱上锐化为能量集中的、清晰的水平线。

FSST的计算是 STFT 的一种“重排”：

首先计算信号 $r~b(t)\tilde{r}_{b}(t)$ 的 STFT：

$Zr~b(t)f(t,ω)=∫Rr~b(τ)f∗(τ−t)e−jωτdτZ_{\tilde{r}_{b}(t)}^{f}(t,\omega)=\int_{\mathbb{R}}\tilde{r}_{b}(\tau)f^{*}(\tau-t)e^{-j\omega\tau}d\tau$
然后，计算 STFT 的“质心”（瞬时频率估计）：

$ω^r~b(t)(t,ω)=ω−ℑ ⁣{Zr~b(t) f′(t,ω)Zr~b(t) f(t,ω)} \hat{\omega}_{\tilde r_b(t)}(t,\omega) = \omega - \Im\!\left\{\frac{ Z_{\tilde r_b(t)}^{\,f'}(t,\omega) }{ Z_{\tilde r_b(t)}^{\,f}(t,\omega) } \right\}$

最后，通过将 STFT 能量 $Z$ 重新分配到其质心 $ω^\hat{\omega}$ 位置，得到高分辨率的 FSST 谱 $λb(t,ω)\lambda_{b}(t,\omega)$ 。

B. 干扰检测 (Hough 变换)

获得T-F谱后，算法将其视为一幅图像，并开始应用图像处理技术。

边缘检测 ：首先使用 Canny 边缘检测器从T-F谱图像中提取边缘，得到 $E (x, y)$ 。边缘检测本身不足以定位清晰的线条，它通常只输出一堆离散的短线。
霍夫变换 (HT) ：对边缘图像 $E (x, y)$ 应用霍夫变换。HT 是一种强大的技术，擅长在噪声中检测不连续的直线。它通过一个极坐标变换，将 $(x, y)$ 图像空间中的一条线映射到 $(ρ,θ)(\rho, \theta)$ 霍夫参数空间中的一个点：
$ρ=xcos⁡θ+ysin⁡θ\rho=x \cos \theta+y \sin \theta$
其中 $ρ\rho$ 是原点到直线的垂直距离， $θ\theta$ 是该垂直线与x轴的夹角。
斜率滤波 ：这是区分目标和干扰的核心。在T-F谱图像中（时间为x轴，频率为y轴）：
- 目标（水平线）对应 $θ=90∘\theta=90^{\circ}$ 。
- 干扰（倾斜的啁啾线）对应 $θ≠90∘\theta \ne 90^{\circ}$ 。
生成掩码 ：算法通过识别所有 $θ≠90∘\theta \ne 90^{\circ}$ 的线来生成一个干扰掩码 $E_m(x,y)$ 。

C. 时频脊重建

最简单粗暴的方法是直接用这个掩码将T-F谱中的干扰样本“置零”。但这种“硬置零”操作存在一个严重问题：如果目标和干扰在时频上重叠（即线条交叉），那么置零操作也会擦除有用的目标回波信号，导致目标功率损失和检测性能下降。

为了解决这个问题，本文提出使用时频脊（Time-Frequency Ridge）重建这一巧妙的步骤。

初步置零：首先，使用 B 步骤中的干扰掩码 $E_m$ 对T-F谱进行置零操作，得到 $R^b,z(t,ω)\hat{R}_{b,z}(t,\omega)$ 。此时干扰消失了，但目标线也变得“残缺不全”。
提取时频脊：在置零后的T-F谱上，算法使用“带惩罚的前向-后向贪心算法” 提取能量的主脊（ridge）。这些“脊”代表了剩余的目标信号“骨架”（即瞬时频率的轨迹）。该算法通过最小化一个代价函数来提取脊：
$Wridge(t)=min⁡−ln⁡∣R^b,z(t,ω)∣W_{ridge}(t)=\min - \ln |\hat{R}_{b,z}(t, \omega) |$
该算法会惩罚频率跳变，确保提取出的“脊”是连续的。
信号恢复（关键）：算法并不使用这个残缺的“脊”作为最终结果。而是利用这些提取出的“脊”的索引（位置），返回到步骤1之前
的、原始的、未置零的T-F谱中，精确地将在这些“脊”位置的完整信号幅度提取出来。
逆变换：最后，对这个重建后的、干净的T-F谱应用逆 FSST（ifsst），得到时域中已减轻干扰的信号 $r^b(t)\hat{r}_{b}(t)$ 。

在实现上，该算法使用MATLAB函数 fsst, hough, houghpeaks, houghlines 和 tfridge 来完成。

性能评估与结果

作者通过仿真验证了 HTFR 算法的性能，并与三种SOTA（state-of-the-art）方法进行了比较：ANC, SPARKLE, 和 WD (小波去噪)。

仿真参数

雷达参数 (Table I) ：载频 77 GHz, 带宽 540 MHz, 啁啾周期 45 μs, 采样率 22 MHz。
目标设置 ：4个目标。 $R = [10, 16, 30, 50]$ m, $V = [10, 5, - 5, 0]$ m/s。
干扰设置 ：2个干扰雷达。 $Q = 2$ , $β1=1.5μ\beta_1=1.5\mu$ , $β2=2μ\beta_2=2\mu$ 。

评估指标
使用输出信干噪比 ( $SINR_O$ ) 和相关系数 ( $σ\sigma$ ) 。两者都是越高越好。
$SINRO=20log⁡10∣∣xb∣∣2∣∣xb−r^b∣∣2SINR_{O}=20 \log 10 \frac{||x_{b}||_{2}}{||x_{b}-\hat{r}_{b}||_{2}}$
$σ=xbHr^b∣∣xb∣∣2⋅∣∣r^b∣∣2\sigma=\frac{{x_{b}}^{H}\hat{r}_{b}}{||x_{b}||_{2}\cdot||\hat{r}_{b}||_{2}}$

HTFR 算法步骤图示 (图 1)

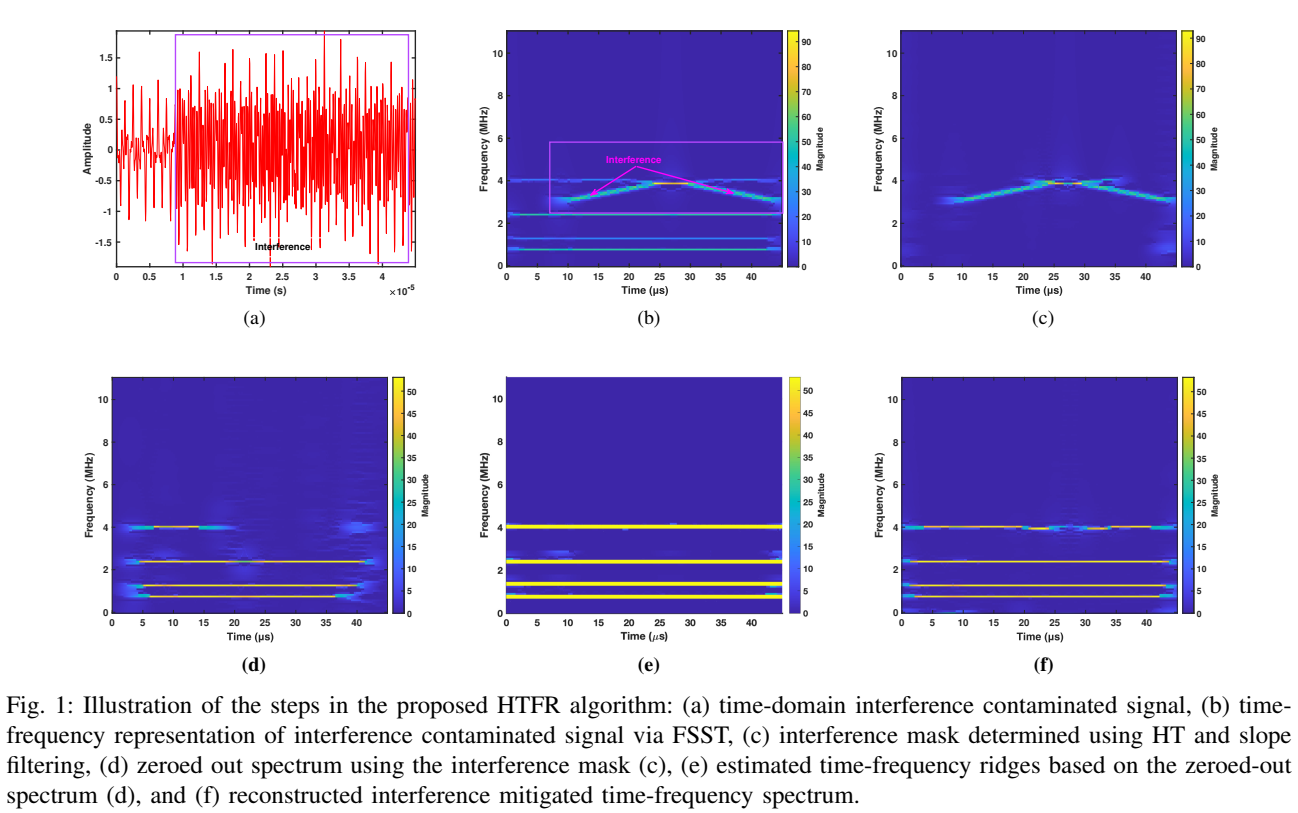
图 1 直观地展示了整个 HTFR 的处理流程：

(a) 时域受污染信号 ：显示了原始信号，其中约80%被干扰覆盖，输入SINR仅为 -4.78 dB。
(b) 原始T-F谱 (FSST) ：清晰地显示了四个水平线（目标）和两个交叉的斜线（干扰，高亮框内）。
© 干扰掩码 ：由HT和斜率滤波生成的掩码，仅包含斜线（干扰）。
(d) 置零后的T-F谱 ：应用©掩码后，干扰被移除，但目标线也出现了断点（功率损失）。
(e) 提取时频脊 ：在(d)的基础上提取出的目标信号“骨架”（黄线）。
(f) 重建后的T-F谱 ：利用(e)的脊索引，从(b)中恢复目标信号。结果显示，干扰被完全抑制，而四个目标线被完美重建。

方法对比 (图 2, 图 4, 表 II)

图 2：距离剖面图

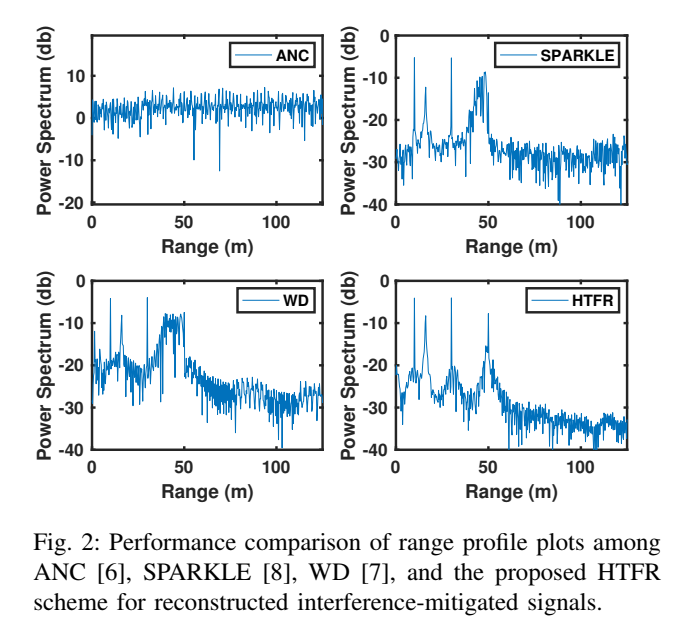
此图显示了不同方法处理后信号的距离维FFT结果。

HTFR（右下）准确地检测到了全部四个目标峰值，且噪声基底非常低。
SPARKLE（右上）在50m处有明显的残余干扰。
ANC（左上）和 WD（左下）性能较差，目标峰值被噪声和残余干扰淹没。

图 4：距离-多普勒图

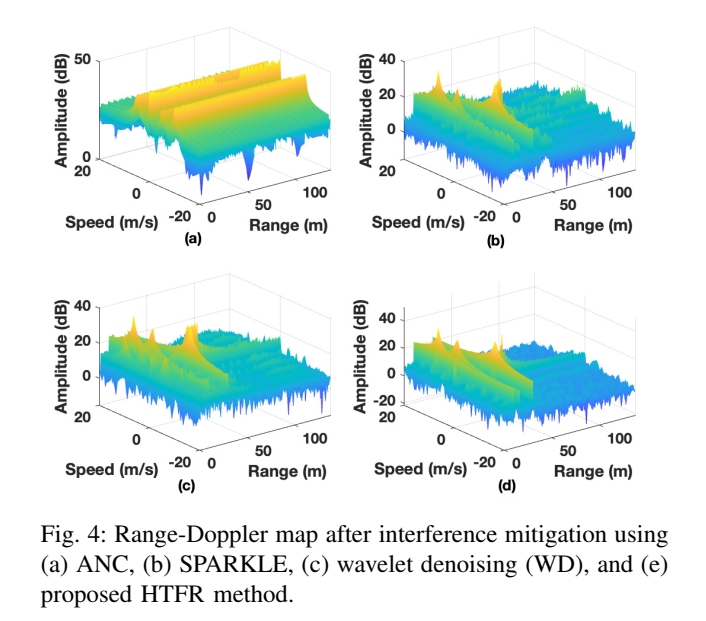
在R-D图上，HTFR（d）同样表现最好，四个目标清晰可见。而 SPARKLE 和 WD（b, c）由于干扰残留，导致50m处的目标无法被检测。ANC（a）性能最差，目标完全不可见。

表 II：定量性能对比

这张表提供了数据（测试平台：Apple M1, 8GB RAM）：

方法	输出 $SINR_O$ (dB)	相关系数 ( $σ\sigma$ )	CPU 时间 (s)
ANC	-6.5427	0.0072	0.02
SPARKLE	5.2731	0.8392	1.61
WD	0.8792	0.7324	0.29
HTFR (本文)	14.5351	0.9823	0.13

结果非常明显：

性能：HTFR 在 $SINR_O$ (14.53 dB) 和相关系数 (0.9823) 两个指标上均显著优于所有其他方法。
效率：HTFR (0.13秒) 的计算速度比 SPARKLE (1.61秒) 和 WD (0.29秒) 更快。虽然 ANC 最快 (0.02秒)，但其性能几乎无效。这表明 HTFR 具有实时处理的潜力。

抗噪声性能 (图 3)

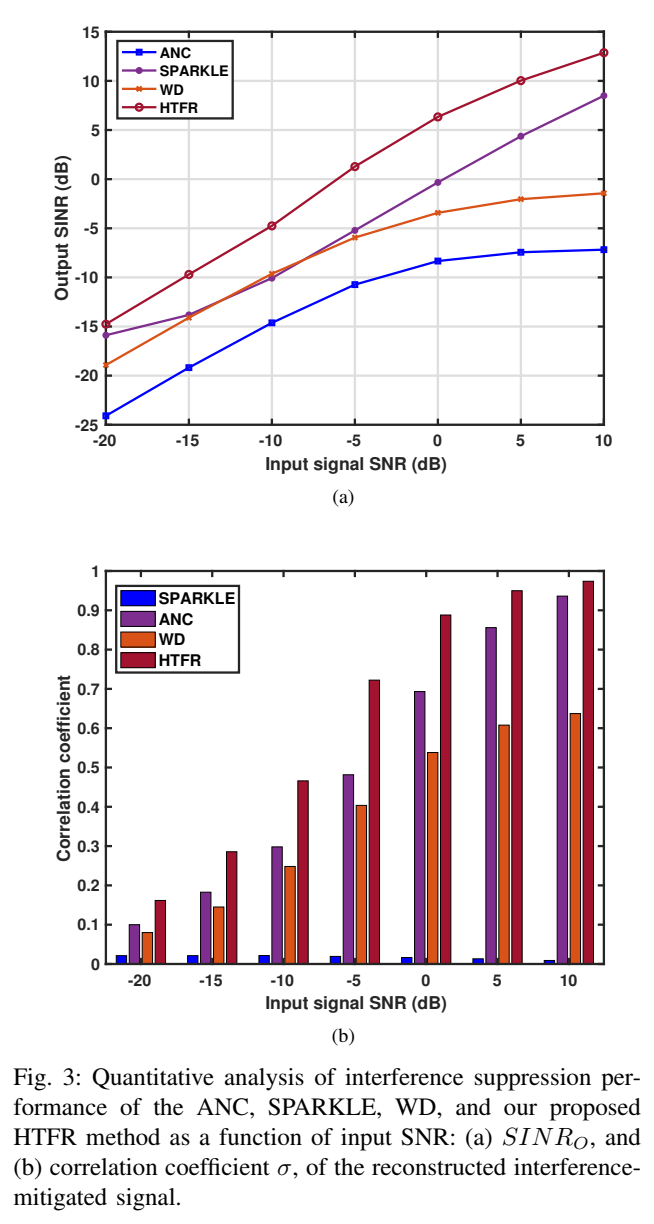
作者还测试了不同输入信噪比（SNR）下的性能。图 3 (a) 和 (b) 显示，在-20 dB到10 dB的所有SNR区间内，HTFR（红线）的输出SINR和相关系数始终全面高于其他三种方法。

结论

本文提出了一种用于FMCW雷达干扰抑制的 HTFR 算法。该方法巧妙地将在T-F谱上区分目标（水平线）和干扰（斜线）的问题，转化为了一个图像处理问题。它利用霍夫变换和斜率滤波来识别干扰，并创新性地使用时频脊重建来恢复被干扰掩盖的目标信号，避免了传统“置零”方法带来的目标功率损失。

仿真结果表明，HTFR 无论是在输出SINR、相关系数，还是在距离-多普勒图的直观检测上，均显著优于ANC、SPARKLE和WD等SOTA方法，同时保持了较高的计算效率，使其成为一种适用于自动驾驶雷达的、有前景的干扰抑制方案。

附录：数学推导

本文的核心前提是“目标是单音，干扰是啁啾”。这个结论在论文中是作为已知条件给出的。这里的附录将提供这一关键结论的推导。

推导1：目标回波 $x_b(t)$ 为何是“单音”

我们从混频的相位开始推导。为简化，我们只考虑一个静止目标，其延迟为 $τ=2Rc\tau = \frac{2R}{c}$ 。

发射信号相位 $ϕT(t)\phi_T(t)$ ：
$ϕT(t)=2π(fot+12μt2)\phi_T(t) = 2\pi(f_o t + \frac{1}{2}\mu t^2)$
接收信号相位 $ϕR(t)\phi_R(t)$ ：
$ϕR(t)=ϕT(t−τ)=2π(fo(t−τ)+12μ(t−τ)2)\phi_R(t) = \phi_T(t-\tau) = 2\pi(f_o (t-\tau) + \frac{1}{2}\mu (t-\tau)^2)$
混频（解啁啾）：拍频信号 $x_b(t)$ 的相位 $ϕb(t)\phi_b(t)$ 是接收相位与发射相位共轭（即负相位）之和：
$ϕb(t)=ϕR(t)−ϕT(t)\phi_b(t) = \phi_R(t) - \phi_T(t)$
$ϕb(t)=2π[(fo(t−τ)+12μ(t−τ)2)−(fot+12μt2)]\phi_b(t) = 2\pi [ (f_o (t-\tau) + \frac{1}{2}\mu (t-\tau)^2) - (f_o t + \frac{1}{2}\mu t^2) ]$
展开与化简：
$ϕb(t)=2π[(fot−foτ+12μ(t2−2tτ+τ2))−fot−12μt2]\phi_b(t) = 2\pi [ (f_o t - f_o \tau + \frac{1}{2}\mu(t^2 - 2t\tau + \tau^2)) - f_o t - \frac{1}{2}\mu t^2 ]$
我们消去 $f_o t$ 和 $12μt2\frac{1}{2}\mu t^2$ 项：
$ϕb(t)=2π[−foτ−μtτ+12μτ2]\phi_b(t) = 2\pi [ -f_o \tau - \mu t \tau + \frac{1}{2}\mu \tau^2 ]$
瞬时频率：频率是相位的导数。我们对 $ϕb(t)\phi_b(t)$ 求导，得到瞬时拍频 $f_b(t)$ ：
$fb(t)=12πdϕb(t)dt=12πddt(2π[−foτ−μtτ+12μτ2])f_b(t) = \frac{1}{2\pi} \frac{d\phi_b(t)}{dt} = \frac{1}{2\pi} \frac{d}{dt} ( 2\pi [ -f_o \tau - \mu t \tau + \frac{1}{2}\mu \tau^2 ] )$
$fb(t)=−μτf_b(t) = -\mu \tau$
结论：拍频 $f_b$ 是一个常数（因为它只取决于 $μ\mu$ 和 $τ\tau$ ，这两者都是常数）。这证明了目标回波在混频后是一个单音（或正弦）信号，在T-F谱上表现为一条水平线。

注：式中的 $−foτ-f_o \tau$ 是初始相位， $12μτ2\frac{1}{2}\mu \tau^2$ 是“残余视频相位”，通常很小。如果目标在移动， $τ\tau$ 会随 $t$ 变化（ $τ(t)=2(Rm+Vmt)c\tau(t) = \frac{2(R_m+V_m t)}{c}$ ），此时 $f_b(t)$ 会额外包含一个多普勒项 $2foVmc\frac{2 f_o V_m}{c}$ 和一个很小的斜率项，但其主要成分 $μτ\mu\tau$ 仍然是常数，因此仍被视为“水平线”。

推导2：干扰信号 $x_{b,int}(t)$ 为何是“啁啾”

现在我们考虑本车雷达混频器 $x^*(t)$ 混入了一个干扰信号 $x_{int}(t)$ 。

本车LO（混频）相位 $ϕLO(t)\phi_{LO}(t)$ ：
$ϕLO(t)=−ϕT(t)=−2π(fot+12μt2)\phi_{LO}(t) = -\phi_T(t) = -2\pi(f_o t + \frac{1}{2}\mu t^2)$
干扰信号相位 $ϕint(t)\phi_{int}(t)$ ：（为简化，忽略延迟 $τ′\tau'$ ）
$ϕint(t)=2π(fqt+12βqt2)\phi_{int}(t) = 2\pi(f_q t + \frac{1}{2}\beta_q t^2)$
干扰拍频相位 $ϕb,int(t)\phi_{b,int}(t)$ ：
$ϕb,int(t)=ϕint(t)+ϕLO(t)\phi_{b,int}(t) = \phi_{int}(t) + \phi_{LO}(t)$
$ϕb,int(t)=2π(fqt+12βqt2)−2π(fot+12μt2)\phi_{b,int}(t) = 2\pi(f_q t + \frac{1}{2}\beta_q t^2) - 2\pi(f_o t + \frac{1}{2}\mu t^2)$
合并同类项：
$ϕb,int(t)=2π[(fq−fo)t+12(βq−μ)t2]\phi_{b,int}(t) = 2\pi [ (f_q - f_o)t + \frac{1}{2}(\beta_q - \mu)t^2 ]$
瞬时频率：对 $ϕb,int(t)\phi_{b,int}(t)$ 求导，得到瞬时干扰拍频 $f_{b,int}(t)$ ：
$fb,int(t)=12πdϕb,int(t)dtf_{b,int}(t) = \frac{1}{2\pi} \frac{d\phi_{b,int}(t)}{dt}$
$fb,int(t)=(fq−fo)+(βq−μ)tf_{b,int}(t) = (f_q - f_o) + (\beta_q - \mu)t$
结论：由于干扰雷达的斜率 $βq\beta_q$ 与本车雷达的斜率 $μ\mu$ 几乎不可能相同（即 $βq≠μ\beta_q \ne \mu$ ），因此 $(βq−μ)≠0(\beta_q - \mu) \ne 0$ 。

这意味着干扰拍频 $f_{b,int}(t)$ 是一个随时间 $t$ 线性变化的函数。这正是啁啾信号（Chirp）的定义。因此，干扰在T-F谱上表现为一条倾斜的线。