3网合一网站天眼企业查询系统官网
58.组合总和 Ⅳ
组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入: nums = [1,2,3], target = 4
输出: 7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入: nums = [9], target = 3
输出: 0
提示:
1 <= nums.length <= 2001 <= nums[i] <= 1000nums中的所有元素 互不相同1 <= target <= 1000
进阶: 如果给定的数组中含有负数会发生什么?问题会产生何种变化?如果允许负数出现,需要向题目中添加哪些限制条件?
根据分析问题的过程中,发现重复子问题,抽象出来一个状态表示
dp[i]表示:凑成总和为i,一共有多少种排列数
dp[0]初始化为1
相当于是起始位置把
直接返回dp[target]
class Solution{public:int combinationSum4(vector<int>& nums, int target){vector<double>dp(target+1);dp[0]=1;for(int i=1;i<=target;i++)//就是每次当我们的和为i的时候,总共的排列数有多少个,就是dp[i]//当遍历到target的时候我们直接利用前面的dp表进行累加操作就行了{for(auto x:nums)//将nums中的数依次取出来,看看是否存在合适的组合{if(i>=x)dp[i]+=dp[i-x];}}return dp[target];}};
- 外层循环
for (int i = 1; i <= target; i++):从 1 到target遍历每个目标值,依次计算组成这些目标值的组合数量。 - 内层循环
for (auto x : nums):遍历数组nums中的每个元素x。 - 条件判断
if (i >= x):只有当当前目标值i大于等于数组中的元素x时,才进行状态转移。 - 状态转移方程
dp[i] += dp[i - x];:对于每个元素x,如果i >= x,那么组成目标值i的组合数量可以由组成目标值i - x的组合数量推导而来。因为只要在组成i - x的每个组合后面加上元素x,就可以得到一个组成i的组合。所以dp[i]要加上dp[i - x]。 return dp[target];:最终返回dp[target],即组成目标值target的组合数量。
就是计算每个位置的dp表,然后后面的dp表是会利用到前面的dp表的,我们进行累加操作就行了
59.不同的二叉搜索树
不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
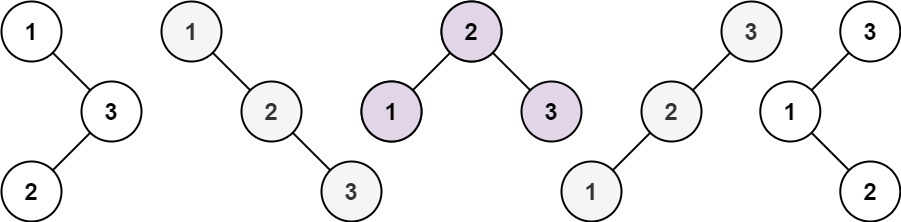
输入: n = 3
输出: 5
示例 2:
输入: n = 1
输出: 1
二叉搜索树:左->根->右
dp[i]表示:节点个数为i个时候,一共有多少种二叉搜索树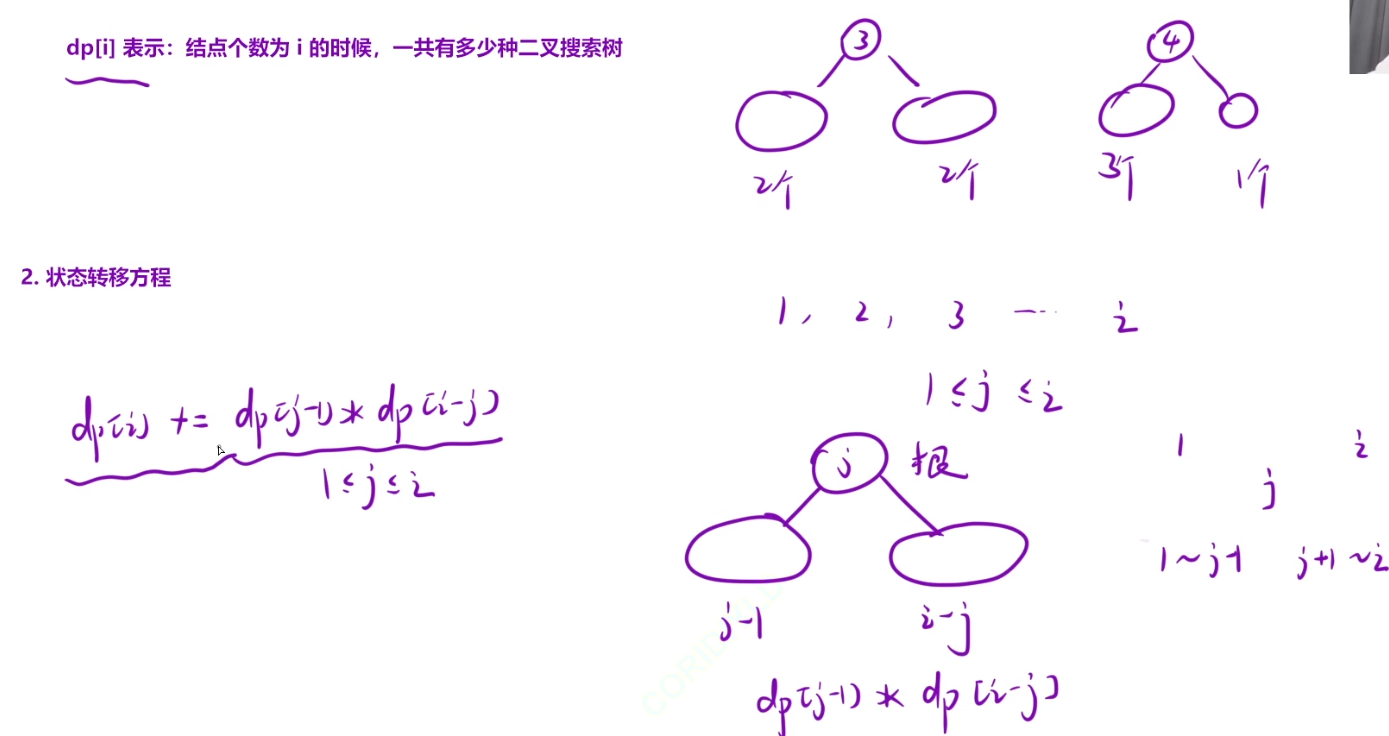
如果我们的j是根的话,因为我们的二叉搜索树是左->根->右,所以我们左边是存在j-1种可能得,右边有i-j种可能得
因为左右是可以相互进行搭配的
所以这个数量就是
dp[i]+=dp[j-1]+dp[i-j]了
dp[0]就是说没有节点,就是空树,空树也是二叉搜索树
所以dp[0]=1
返回值就是dp[n]
class Solution {public:int numTrees(int n){vector<int>dp(n+1);dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++)//枚举根节点{dp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}};
