当前位置：首页 > news >正文

数据结构与算法概述

news 2025/11/9 8:53:59

数据结构是研究非数值计算的程序设计问题中计算机的处理对象以及它们之间的关系和操作等的学科
数据结构是算法的基础，算法的性能又受限于底层的数据结构

一、数据结构术语

数据(Data)是信息的载体

数据元素(Data Element)是数据的基本单位

数据项(Data Item)是组成数据元素的有特定意义、不可分割的最小单位

数据对象(Data Object)是具有相同性质的数据元素的集合

数据处理(Data Processing)是指对数据对象进行操作的过程

数据结构(Data Structure)是指相互之间存在一种或多种特定关系的数据元素的集合

使用二元组表示一种数据结构：
DS(Data_Structure) = ( D , R )

DS表示一种数据结构，D是数据元素的有限集，R是D上二元关系的集合，d表示集合D中的一个数据元素，r是D上一个关系的有限集。（尖括号<>表示有向关系，圆括号()表示无向关系）

数据结构一般分为以下四种：

1.集合结构：属于同一个集合，不存在逻辑关系
Set={D,R}
D={0,1,2,3,4}
R={ }

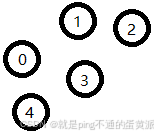
2.线性结构：存在一对一关系
Linear={D,R}
D={d1,d2,d3,d4,d5}
R={r}
r={<d1,d2>,<d2,d3>,<d3,d4>,<d4,d5>}

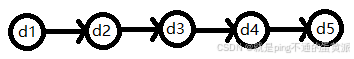
3.树型结构：存在一对多关系
Tree={D,R}
D={d1,d2,d3,d4,d5,d6,d7}
R={r}
r={<d1,d2>,<d1,d5>,<d1,d7>,<d2,d3>,<d2,d4>,<d5,d6>}

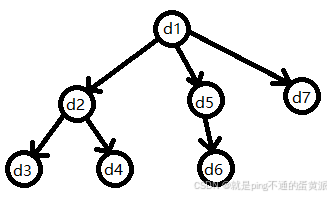
4.图结构：存在多对多关系
Graph={D,R}
D={d1,d2,d3,d4,d5,d6}
R={r}
r={(d1,d2),(d1,d4),(d1,d5),(d2,d3),(d3,d4),(d3,d5),(d4,d6),(d6,d5)}

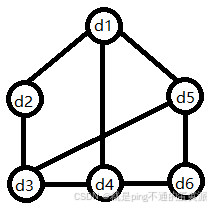
逻辑结构：数据元素之间的逻辑关系
物理结构(存储结构)：数据结构在计算机中的表示，分为顺序存储结构和链式存储结构

二、数据类型和抽象数据类型

类型(Type)是一组具有相同特性的值的集合

数据类型(Data Type)是一组值的集合和定义在这个值上的一组操作的总称，一般包括整数、浮点数、字符、字符串、指针、数组、记录、类、文件等
数据类型可以分为简单类型和结构类型

抽象数据类型(Abstract Data Type, ADT)由一个数据结构和在该数据结构上的一组操作所组成

使用三元组表示抽象数据类型
ADT = ( D , R , P )
ADT是抽象数据类型，D是数据对象，R是D上的关系集合，P是对D的基本操作集
ADT抽象数据类型名{
数据对象：<数据对象的定义>
数据关系：<数据关系的定义>
基本操作：<基本操作的定义>
}
其中数据对象和数据关系的定义为伪码描述，基本操作的定义格式为：
基本操作名(参数表): 操作结果

三、算法和算法分析

算法(Algorithm)是对特定问题求解步骤的一种描述，是指令的有限序列
算法具有：①有穷性 ②确定性 ③可行性 ④输入 ⑤输出
算法的设计要求：①正确性(Correctness) ②可读性(Readability) ③健壮性(Robustness) ④高效性(High Efficiency)

算法的时间复杂度分析的是算法运行时间随着数据量变大时的增长趋势
用"O"表示数量级，T(n)=O(f(n))=O(n)
当问题规模n趋向无穷大时，时间复杂度T(n)的数量级(阶)称为算法的渐进时间复杂度
T(n)=O(f(n))
①可以忽略常数项
②可以省略所有系数
③在循环嵌套时使用乘法
一般考虑的是最坏情况下的时间复杂度

常数阶：频度为1，时间复杂度为O(1)

x++;

线性阶：频度为n，时间复杂度为O(n)

for(i=1;i<=n;++i)x++;

平方阶：频度为n×n，时间复杂度为O(n²)

for(j=1;j<=n;++j)for(k=1;k<=n;++k)x++;

立方阶：频度为n×n×n，时间复杂度为O(n³)

for(i=1;i<=n;i++)for(j=1;j<=n;j++){c[i][j]=0;for(k=1;k<=n;k++)c[i][j]=c[i][j]+a[i][k]*b[k][j];}

对数阶：设频度为f(n)，时间复杂度为O(log₃n)

for(i=1; i<=n; i=i*3)x++;

线性对数阶：外层循环执行log₂n次，内侧循环执行n次，时间复杂度为O(nlog₂n)

for(j=1; j<=n; j*=2)for(k=1; k<=n; ++k)x++;

起泡排序：最好情况下时间复杂度为O(n)，最差情况下时间复杂度为O(n²)

void BubbleSort(RecType R[],int n)
{i=n;while(i>1){lastExchange=1;for(j=1;j<i;j++)if(R[j].key>R[j+1].key){temp=R[j];R[j]=R[j+1];R[j+1]=temp;lastExchange=j;}i=lastExchange;}
}

常见的时间复杂度为：
O(1)＜O(log₂n)＜O(n)＜O(nlog₂n)＜O(n²)＜O(n³)