当前位置：首页 > news >正文

[Java算法] 双指针(1)

news 2025/11/9 8:45:52

1.移动零

解法1:

public class double_pointer_01 {public static void moveZeroes(int[] nums) {int dest = 0;int cur = 0;while(cur<nums.length&&dest<=cur){while(nums[cur]==0&&dest<=cur){cur++;// 防止cur越界（当数组全为0时，cur会超过数组长度）if (cur >= nums.length) {return;}}while(nums[dest]!=0 && dest<cur){dest++;if(dest>cur){return;}}swap(nums,dest,cur);dest++;cur++;}}public static void swap(int[] nums , int dest , int cur){int tmp = nums[dest];nums[dest] = nums[cur];nums[cur] = tmp;}public static void main(String[] args) {int[] nums = {0,1,0,3,12};moveZeroes(nums);for (int x:nums) {System.out.println(x);}}}

解法2 :

public void moveZeroes2(int[] nums){for(int cur = 0,dest = -1;cur < nums.length;cur++){if(nums[cur]!=0) {dest++;swap(nums, dest, cur);}}
}
public static void swap(int[] nums , int dest , int cur){int tmp = nums[dest];nums[dest] = nums[cur];nums[cur] = tmp;
}

运用到快速排序的思想

2.复写零

class Solution {public void duplicateZeros(int[] arr) {int count = 0;int len = arr.length;int cur = 0;for(cur = 0;cur<=len-1;cur++){if(count>=len){break;}if(arr[cur] == 0){count+=2;}else{count++;}}int dest = len-1;cur--;if(count == len+1){arr[dest--] = 0;cur--;}while(cur>=0&&dest>=0){if(arr[cur]!=0){arr[dest--] = arr[cur--];}else{arr[dest--] = 0;arr[dest--] = 0;cur--;}}}
}

算法思路

用 count 来标记统计结束的下标 , cur 找结束的位置 , 如果 cur 是 0 则 cout+2 , 非零加一 ,

cur 回退 1????没懂 , 自己画图没有问题 , 代码跑起来有问题

再判断 count 的长度是否是比 len 多 1(末尾为 0),是则做处理

最后从后往前复写操作

3.快乐数

class Solution {public static boolean isHappy(int n) {if(n == 1||sum_squares(n) == 1){return true;}int slow = sum_squares(n);int fast = sum_squares(sum_squares(n));while(slow != fast){slow = sum_squares(slow);fast = sum_squares(sum_squares(fast));if(slow == 1||fast == 1){return true;}}return false;}public static int sum_squares(int n){int sum = 0;while(n!=0){int tmp = n % 10;sum = sum + tmp*tmp;n /= 10;}return sum;}
}
public class demo2 {public static void main(String[] args) {Solution s = new Solution();boolean a = s.isHappy(19);System.out.println(a);}
}

算法思路

先写出求各给数位上的平方之和的方法
如果 n 为 1 或者各给数位的平方和为 1 (例如 10,100,1000 等)直接返回 true
让 slow 往后走一步(调用一次方法) , 让 fast 往后走两步(调用两次方法).(快慢指针法)
一直到他俩相遇 (此题他们必定会形成一个环(抽屉原理)) , 在循环的过程中如果 slow 或者 fast 的值为 1 , 那么结束循环 , 为快乐数;如果在循环过程中 , 知道 slow 和 fast 相遇都没有变为 1 , 那么不是快乐数

4.盛最多水的容器

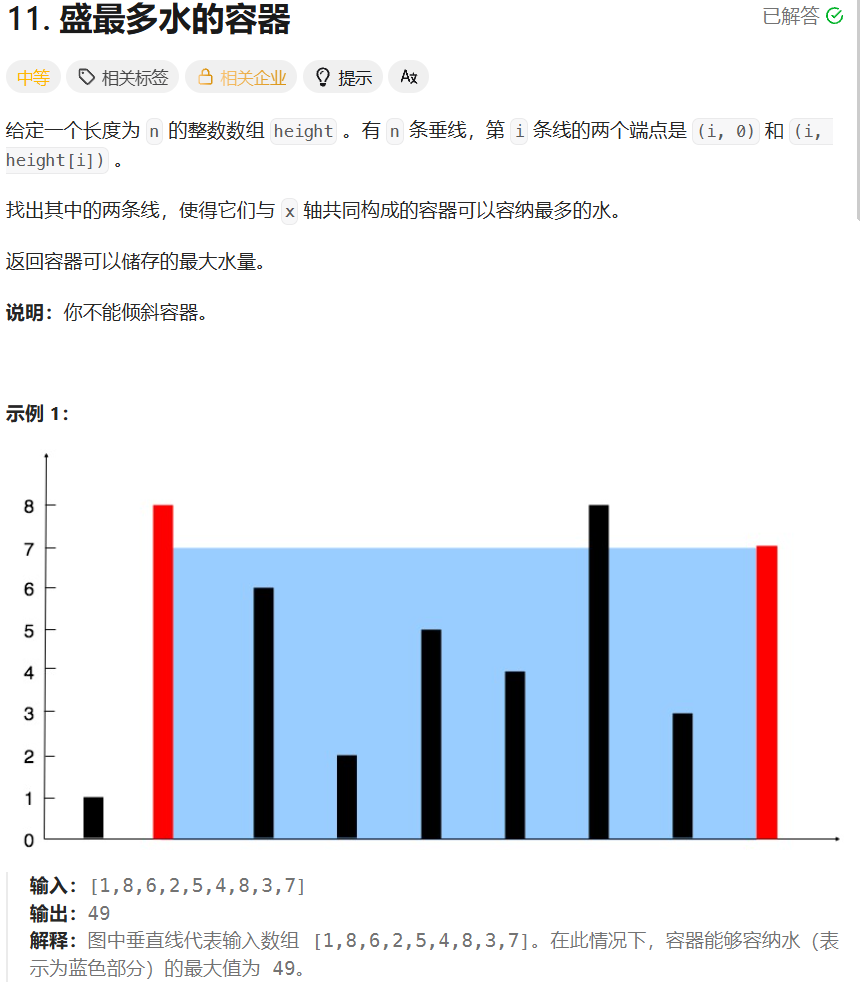
public int maxArea(int[] height) {int left = 0;int right = height.length-1;int len = right-left;int h = (height[left]<height[right])?height[left]:height[right];int maxVolume = len*h;if(height[left]<height[right]){left++;}else{right--;}while(left!=right){len = right-left;h = (height[left]<height[right])?height[left]:height[right];int volume = len*h;maxVolume = (maxVolume>volume)?maxVolume:volume;if(height[left]<height[right]){left++;}else{right--;}}return maxVolume;}

算法思路：

- 初始指针：左指针left在数组起始位置（0），右指针right在数组末尾（height.length-1），此时两指针距离最大。
- 计算当前面积：以两指针距离为底，较短的垂线高度为高，乘积为当前面积。
- 指针移动策略：移动较短垂线的指针（贪心选择）。因为若移动较长垂线，底边长减少，高度不会超过当前较短垂线，面积必然减小；而移动较短垂线可能遇到更高的垂线，从而获得更大面积。
- 循环终止：左右指针相遇（left == right）时，所有可能的组合已遍历。

图解:

5.有效三角形的个数

class Solution {public int triangleNumber(int[] nums) {quickSort(nums ,0, nums.length - 1);int larger = nums.length-1;int count = 0;while(larger>=2){int left = 0;int right = larger-1;while(right>left){if(nums[left]+nums[right]>nums[larger]){count += right-left;right--;}else{left++;}}larger--;}return count;}public void quickSort(int[] arr, int low, int high) {if (low < high) {int pivotIndex = partition(arr, low, high); // 分区，返回基准值的最终位置quickSort(arr, low, pivotIndex - 1); // 递归排序左半部分quickSort(arr, pivotIndex + 1, high); // 递归排序右半部分}}public int partition(int[] arr, int low, int high) {int pivot = arr[high]; // 选最后一个元素作为基准值int i = low - 1; // i记录“小于基准值”区域的右边界for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;// 交换arr[i]和arr[j]，将小于基准的元素移到左半区int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}// 将基准值放到最终位置（i+1的位置）int temp = arr[i + 1];arr[i + 1] = arr[high];arr[high] = temp;return i + 1;}
}

补充 : 当三个数为有序时 , 只需判断两个较小数之和是否大于较大数即可 , 如果两个较小数之和大于较大数则是三角形 , 无需再判断剩下两类

算法步骤：

- 排序：先对数组排序（升序），方便固定最长边并利用双指针寻找有效组合。
- 固定最长边：从数组末尾开始，依次将 nums[larger] 作为最长边（larger 从 n-1 递减到 2，因至少需要 3 条边）。
- 双指针找有效组合：对每个最长边 nums[larger]，用左指针 left=0、右指针 right=larger-1 寻找符合 nums[left] + nums[right] > nums[larger] 的组合：