计算机图形学·11 变换（Transformations）

本文是记录专业课“计算机图形学”的部分笔记，参考教材为Angel的第八版交互式计算机图形学——基于WebGL 2.0的自顶向下方法。

1、所谓变换就是把点映射到其它点，把向量映射到其它向量。在一般连续变换、非线性变换中，直线的像不再是直线（直线的像是由直线上每个点的像构成的），而是一条连续曲线。或者我们可以说，当变换是连续一般变换时，直线的像就是一条连续曲线。
2、线性变换条件是f(αp+βq)=αf(p)+βf(q)，满足可加性和齐次性，可以表示为矩阵相乘的形式v=AT u，具有二种形式（标架的变换，或顶点在同一个标架里的坐标变换）。而仿射变换（Affine Transformations）是具有线性不变性的变换，即先经系统再求和和先求和再经系统结果一样。

图形学中的重要性在于，此时我们只需要变换线段的两个端点，而由系统自动画出变换后两个端点间的线段。那么为什么需要变换？可以建模造型（如组合场景：从建模系统局部坐标到某个应用系统物理世界全局坐标）、构造三维场景、实现分形、实现观察与动画。
3、仿射变换的流水线实现如下图所示：

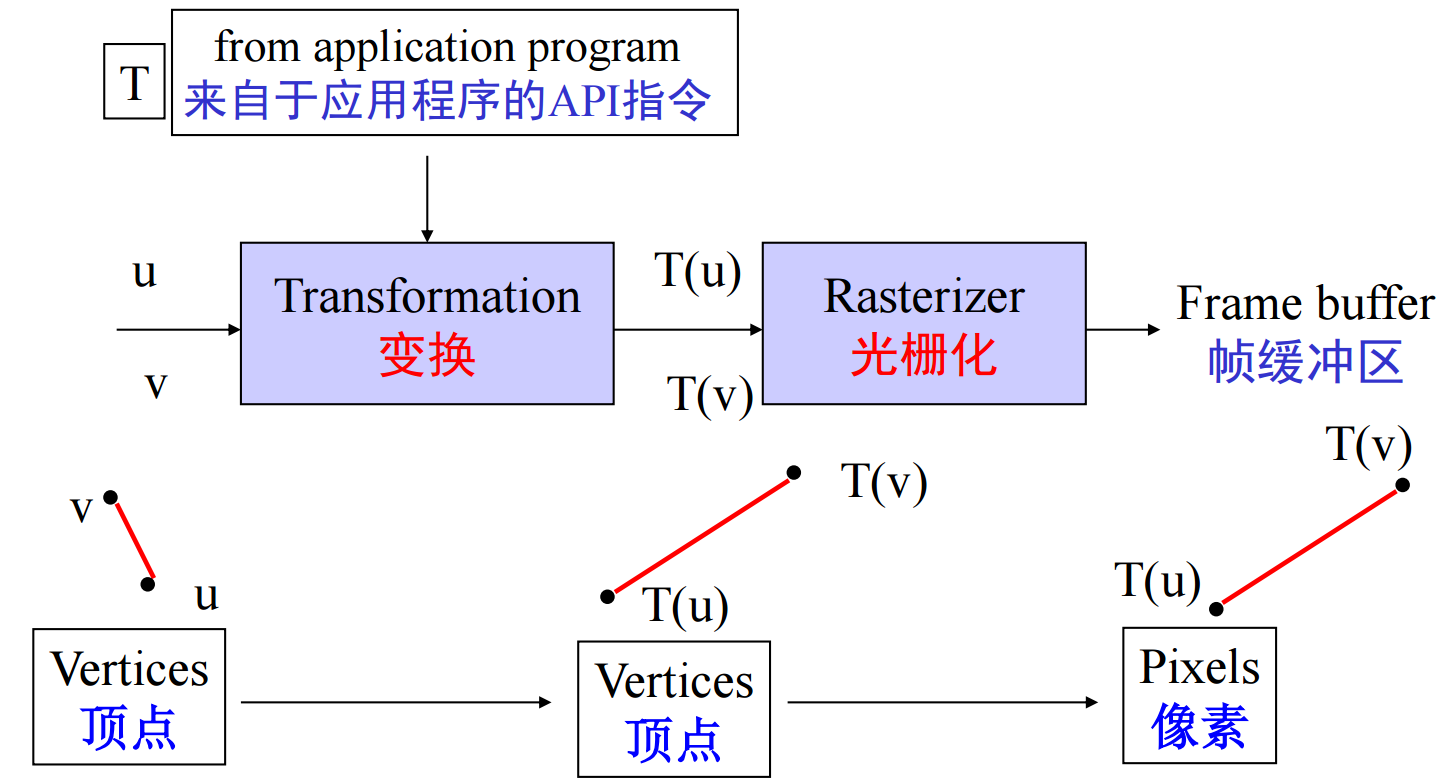
在后面的处理中，我们既会考虑变换的坐标无关的表示（满足物理要求），也会考虑变换在特定标架下的表示（满足计算要求）。
4、我们先来看平移（Translation）。简单来讲就是把一个点移到新的位置，平移量由一个向量d确定，具有三个自由度：P’ = P + d。一般来讲，我们直接把一个对象上的所有点沿同一向量平移。

5、而对于旋转（Rotation），我们先考虑绕原点的二维旋转，比如说逆时针旋转即半径保持不变，角度增加了θ：

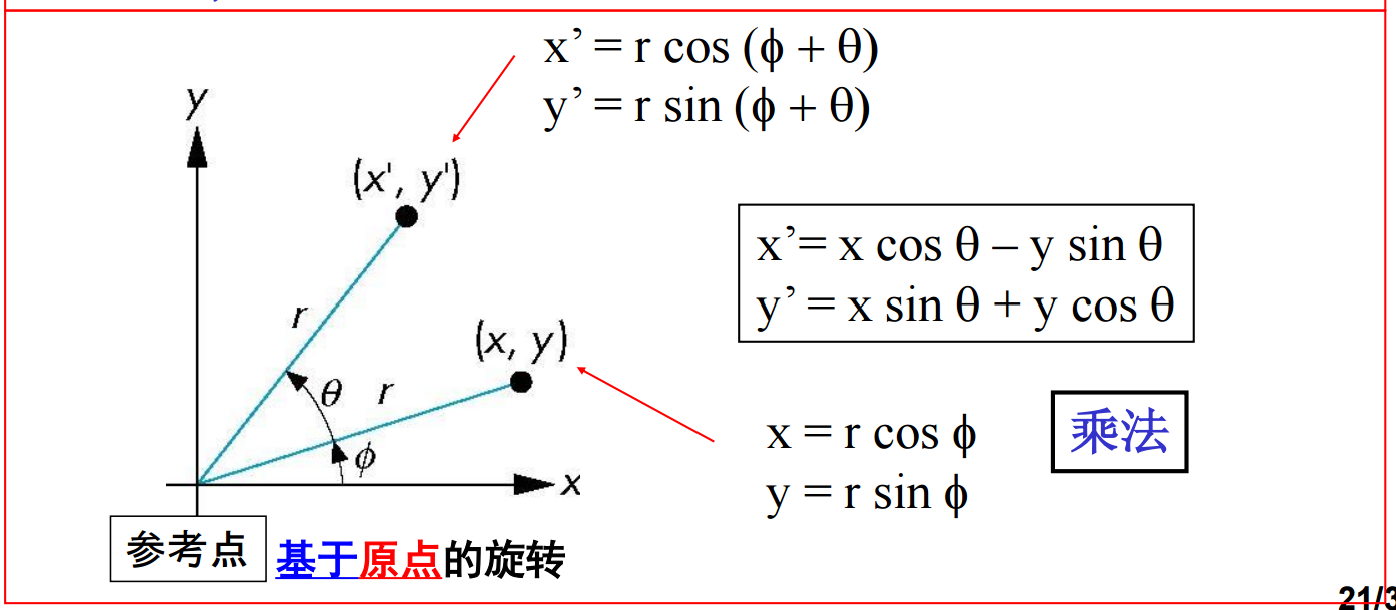
扩展到三维，考虑绕z轴旋转，点的z坐标不变，等价于在 z=常数的xy平面上进行二维旋转（x’=x cosθ –y sinθ、y’ = x sinθ + y cosθ、z’ =z），其齐次坐标表示为p’ = Rz (θ) p：

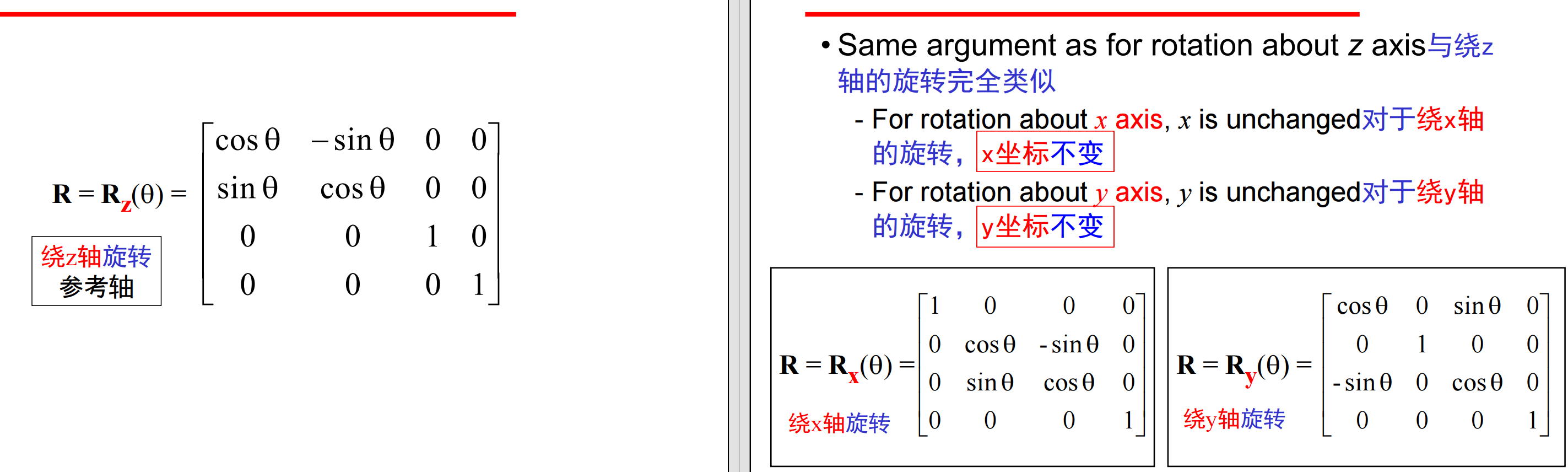
6、旋转与平移是两种刚体变换，这两种变换的复合只能改变对象的位置与定向；其他的仿射变换会改变对象的形状（如放缩、错切），但仍然是仿射变换（保持直线、保持比例、不保角度）。我们来看放缩（Scaling），放缩变换必有一个不动点，其由一个不动点、一个放缩方向以及沿该方向的放缩因子（scale factors）定义，当放缩因子大于1时对象在该方向上变长。

此外，虽然可以利用通用公式计算变换矩阵的逆，但根据几何意义可以直接给出各种变换矩阵的逆。如平移 T^-1(dx, dy, dz) = T(-dx, -dy, -dz) 、旋转R^-1(θ) = R(-θ) （注意到逆矩阵=转置矩阵）、放缩S^-1(sx, sy, sz) = S(1/sx, 1/sy, 1/sz)
7、错切（Shear）是另外一种实用的基本变换，等价于把面向相反方向倾斜（可以想象成正方体的上平面被向右推，前侧面变成了平行四边形）。

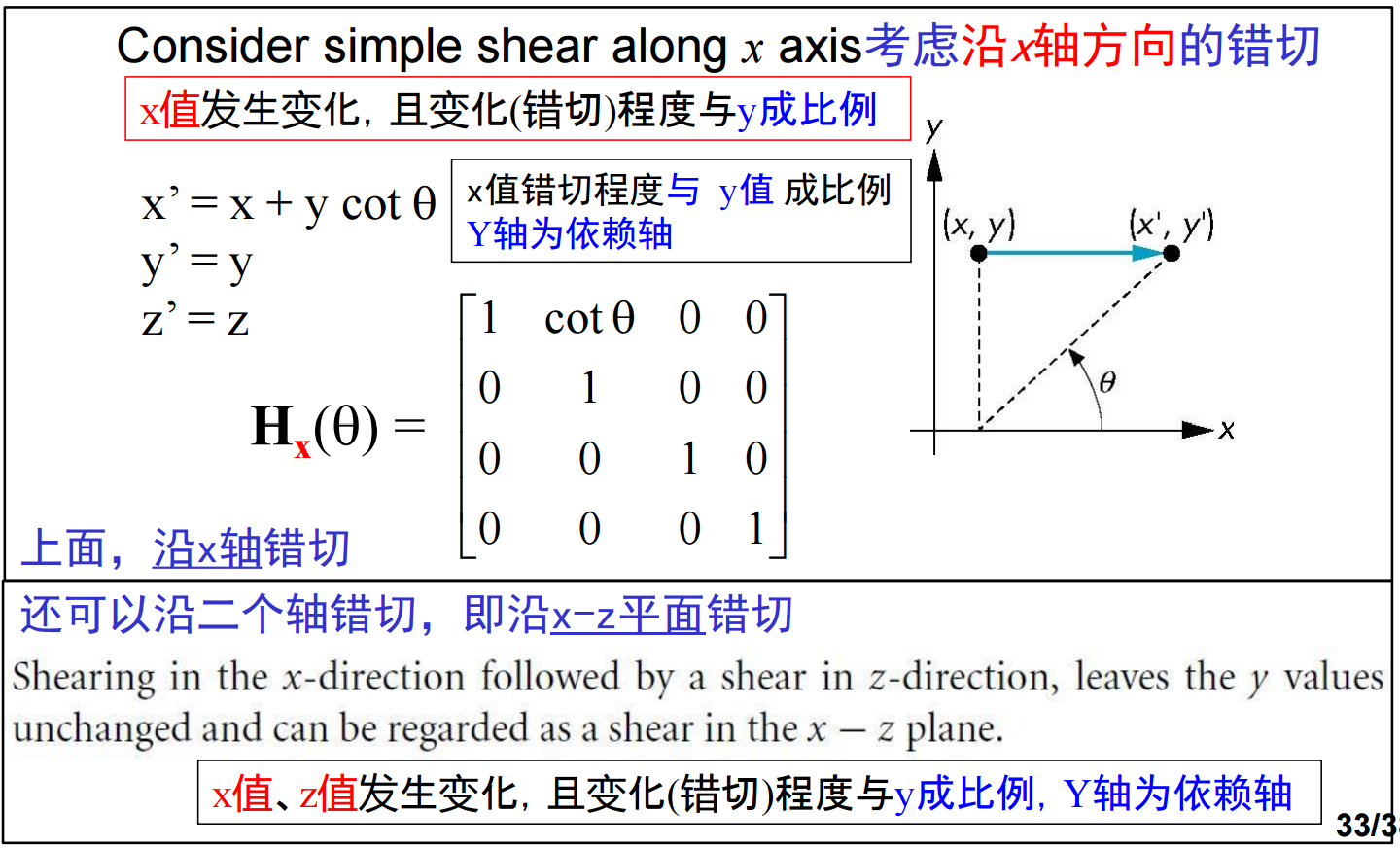
8、仿射变换：平移、旋转、放缩、剪切、反射。我们可以通过把旋转、平移与放缩矩阵相乘，从而形成任意的仿射变换。由于对许多顶点应用同样的变换，因此构造矩阵M = ABCD的代价相比于对许多顶点p计算Mp的代价是很小的，难点在于如何构造出满足要求的变换矩阵。在变换矩阵中，注意，在右边的矩阵是首先被应用的矩阵，不可交换！