基于SMPC随机模型预测控制的IEEE6电网系统matlab仿真,对比不允许负荷响应和允许负荷响应
目录
1.课题概述
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
5.完整工程文件
1.课题概述
实现了一个基于随机模型预测控制SMPC的IEEE6节点电网系统调度方案,核心目标是在含20台风机的风电场接入电网后,通过预测控制优化发电与负荷的功率分配,最小化运行成本。系统以风电场状态空间模型为基础,结合IEEE6节点电网的拓扑与参数,通过滚动优化处理风电随机性,并对比了“允许负荷响应”与“不允许负荷响应”两种场景的经济性差异。
2.系统仿真结果
3.核心程序与模型
版本:Matlab2024b
%x(k+1) = A*x(k) + B*u(k) + G*w(k)
%y(k) = C*x(k) + D*u(k) + v(k)
%Xs1 <= x(k) <= Xe1
%Xs2 <= u(k) <= Xe2
N = 20;%20个风机
p = 3;%每个风机3个状态
Np = N*p;%IEEE6网络节点数据
%system MVA base
baseMVA = 100;
%bus data
% bus_i type Pd Qd Gs Bs area Vm Va baseKV zone Vmax Vmin
bus = [1 3 0 0 0 0 1 1.05 0 230 1 1.05 1.05;2 2 0 0 0 0 1 1.05 0 230 1 1.05 1.05;3 2 0 0 0 0 1 1.07 0 230 1 1.07 1.07;4 1 70 70 0 0 1 1 0 230 1 1.05 0.95;5 1 70 70 0 0 1 1 0 230 1 1.05 0.95;6 1 70 70 0 0 1 1 0 230 1 1.05 0.95;];
%generator data
% bus Pg Qg Qmax Qmin Vg mBase status Pmax Pmin Pc1 Pc2 Qc1min Qc1max Qc2min Qc2max ramp_agc ramp_10 ramp_30 ramp_q apf
gen = [1 0 0 100 -100 1.05 100 1 200 50 0 0 0 0 0 0 0 0 0 0 0;2 50 0 100 -100 1.05 100 1 150 37.5 0 0 0 0 0 0 0 0 0 0 0;3 60 0 100 -100 1.07 100 1 180 45 0 0 0 0 0 0 0 0 0 0 0;];%branch data
% fbus tbus r x b rateA rateB rateC ratio angle status angmin angmax
branch = [1 2 0.1 0.2 0.04 40 40 40 0 0 1 -360 360;1 4 0.05 0.2 0.04 60 60 60 0 0 1 -360 360;1 5 0.08 0.3 0.06 40 40 40 0 0 1 -360 360;2 3 0.05 0.25 0.06 40 40 40 0 0 1 -360 360;2 4 0.05 0.1 0.02 60 60 60 0 0 1 -360 360;2 5 0.1 0.3 0.04 30 30 30 0 0 1 -360 360;2 6 0.07 0.2 0.05 90 90 90 0 0 1 -360 360;3 5 0.12 0.26 0.05 70 70 70 0 0 1 -360 360;3 6 0.02 0.1 0.02 80 80 80 0 0 1 -360 360;4 5 0.2 0.4 0.08 20 20 20 0 0 1 -360 360;5 6 0.1 0.3 0.06 40 40 40 0 0 1 -360 360;
];
gencost = [2 0 0 3 0.00533 11.669 213.1;2 0 0 3 0.00889 10.333 200;2 0 0 3 0.00741 10.833 240;
];..................................................................................
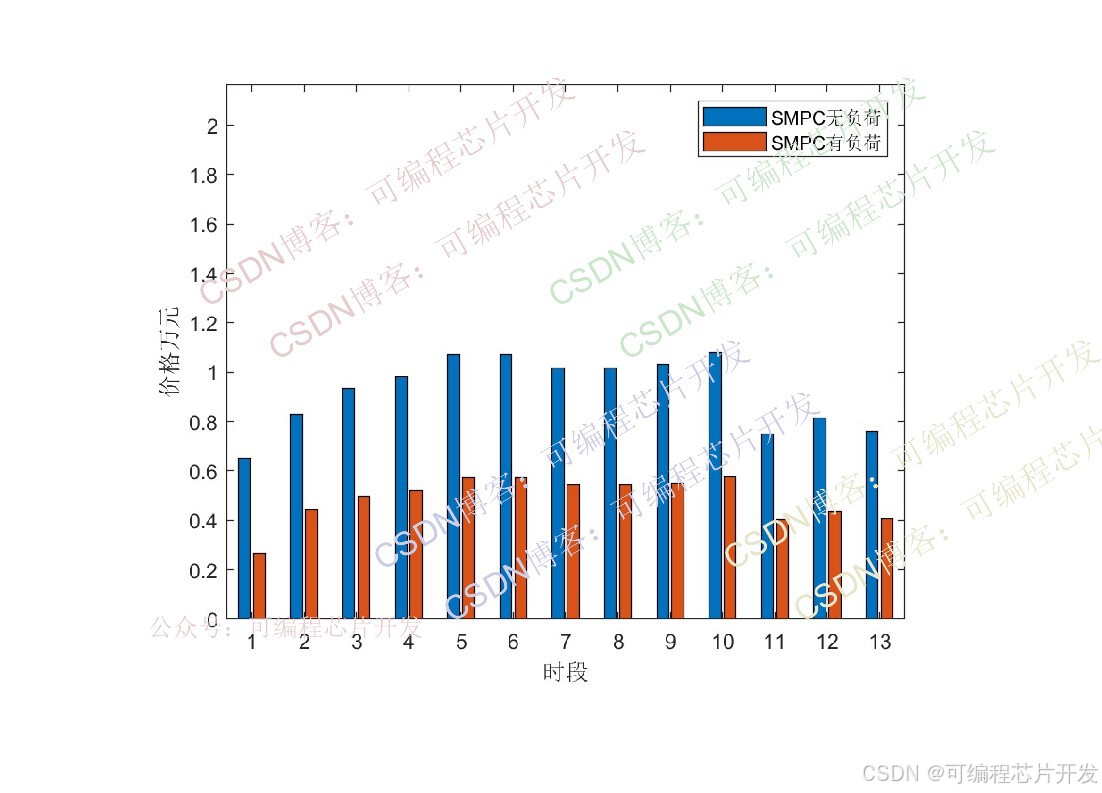
x=[moneya2(1:25:end)',moneya1(1:25:end)'];
figure;
bar(x);
xlabel('时段');
ylabel('价格万元');
legend('SMPC无负荷','SMPC有负荷');
ylim([0,2*max(moneya2)]);figure;
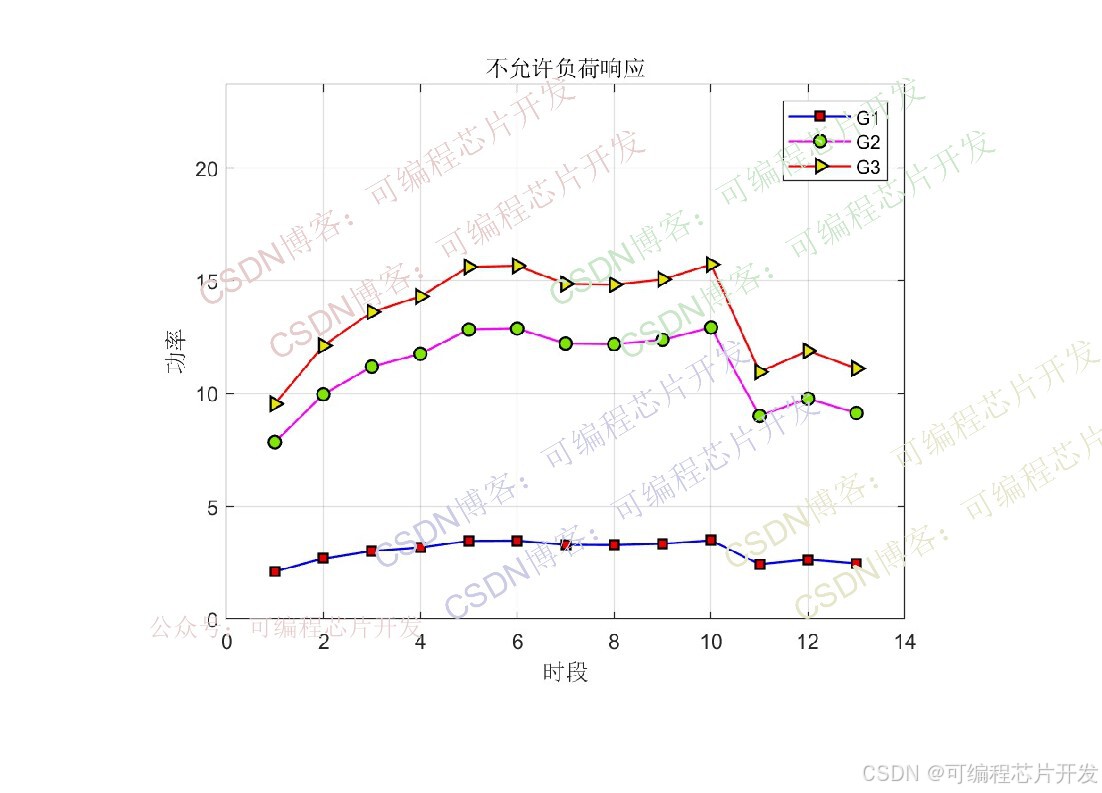
plot(G1(1:25:end)/1e3,'-bs',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
plot(G2(1:25:end)/1e3,'-mo',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.5,0.9,0.0]);
hold on
plot(G3(1:25:end)/1e3,'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);
grid on
legend('G1','G2','G3');
title('不允许负荷响应');
ylim([0,1.5*max(max([G1,G2,G3]))/1e3]);
xlabel('时段');
ylabel('功率');figure;
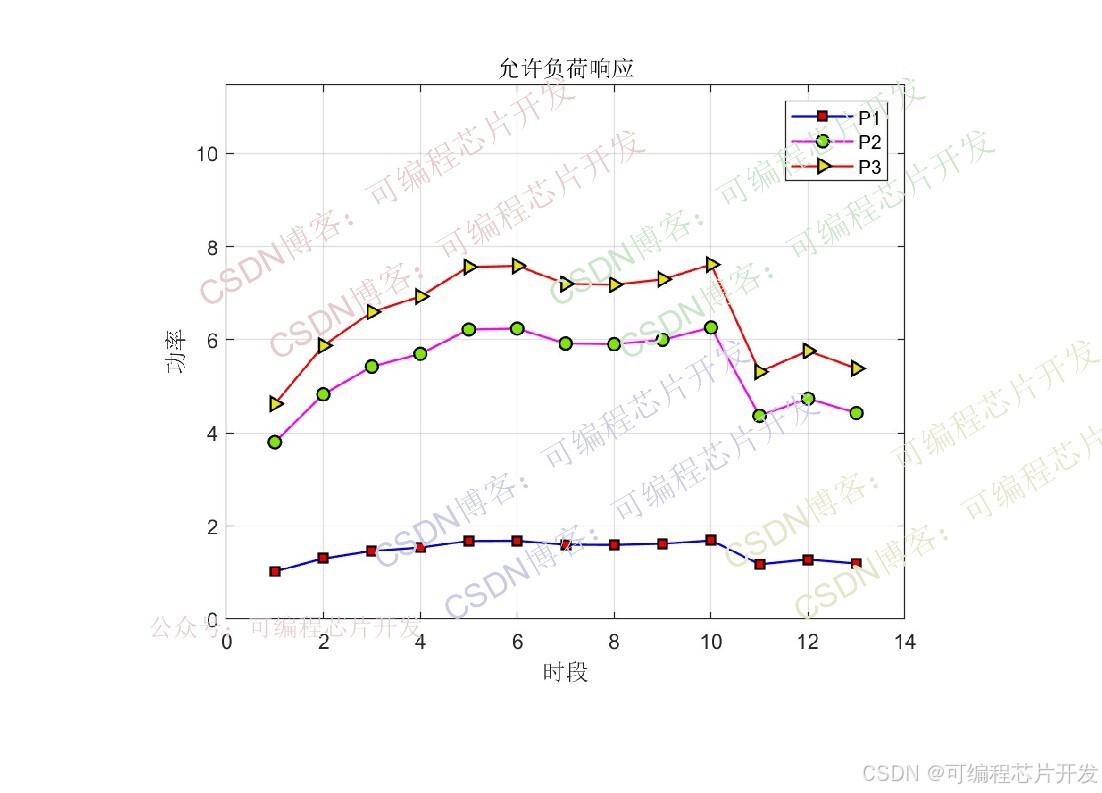
plot(P1(1:25:end)/1e3,'-bs',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
plot(P2(1:25:end)/1e3,'-mo',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.5,0.9,0.0]);
hold on
plot(P3(1:25:end)/1e3,'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);
grid on
legend('P1','P2','P3');
title('允许负荷响应');
ylim([0,1.5*max(max([P1,P2,P3]))/1e3]);
xlabel('时段');
ylabel('功率');
08_099bm4.系统原理简介
SMPC通过建立系统的随机状态空间模型,在每个控制周期内预测未来有限时域内的系统状态与输出,结合随机扰动(如风速波动)的统计特性,求解带约束的二次规划问题,得到当前最优控制量。与确定性MPC不同,SMPC引入扰动的协方差矩阵,在优化过程中考虑不确定性的影响,提高控制鲁棒性。
风电场状态空间模型
程序中,风电场被建模为离散时间随机状态空间系统:

IEEE6电网
电网模型基于IEEE6节点标准测试系统,包含:
节点数据:6个节点中,节点1为平衡节点(type=3),节点2-3为PV节点(type=2),节点4-6为 PQ节点(type=1),定义了有功/无功负荷(Pd、Qd)、电压上下限(Vmax、Vmin)等;
发电机数据:3台发电机分别接入节点1-3,包含有功出力(Pg)、无功上下限(Qmax、Qmin)、调节速率(ramp_agc 等);
支路数据:11条输电线路,定义了电阻(r)、电抗(x)、传输容量(rateA)等;
成本数据:发电机的二次成本函数,如0.00533*Pg² + 11.669*Pg + 213.1,为经济调度提供依据。
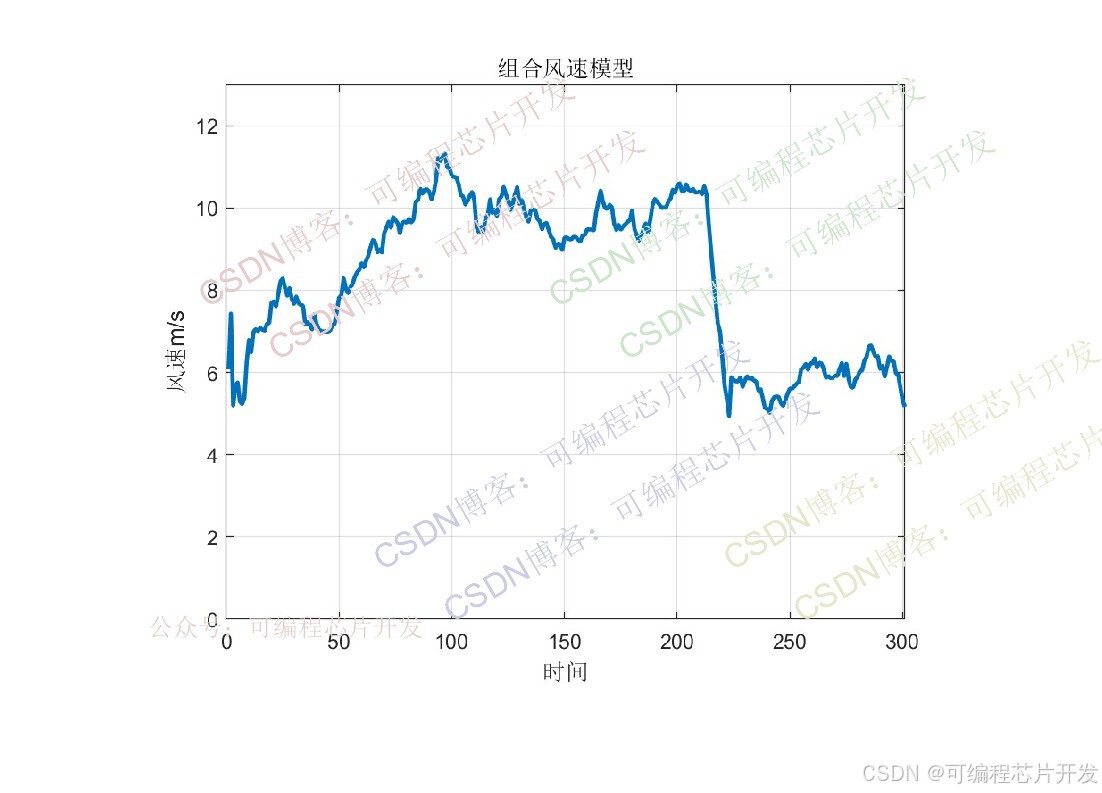
风速通过组合模型

该系统基于SMPC实现了含风电场的IEEE6节点电网优化调度,核心步骤包括状态空间建模、LQR反馈设计、预测约束处理与二次规划优化。对比结果表明,允许负荷响应能有效降低系统运行成本,尤其在高负荷或高电价阶段,负荷与发电的协同优化可显著提升经济性。
5.完整工程文件
v v
关注后,GZH回复关键词:a8
