【信息安全毕业设计】基于zkSNARK与递归证明的数字签名验证方案研究

选题意义背景

在数字信息时代，随着区块链技术、分布式系统和去中心化应用的快速发展，传统数字签名方案在隐私保护、验证效率和安全性方面面临着严峻挑战，随着Web3.0和元宇宙概念的兴起，对数字签名的要求不再仅限于简单的身份认证，更强调隐私保护、效率提升和功能扩展。零知识证明作为一种特殊的密码学工具，允证者向验证者证明某个声明为真，而无需泄露任何额外信息。这一特性使其在保护隐私的同时进行有效验证方面具有独特优势。

传统门限签名方案虽然能够实现多方协作签名，但在匿名性和可追溯性方面存在权衡，现有门限签名方案往往无法同时满足强匿名性和高效可追溯性的需求，这限制了其在需要问责机制的场景中的应用。同时，随着区块链网络的规模扩大，签名验证的计算和存储开销呈指数级增长， 主流公链的交易验证延迟已成为影响用户体验的关键因素。

数据集

数据集主要来源于三个方面：公开的密码学测试数据集、合成的签名数据以及真实的区块链交易数据。为了进行方案的训练、验证和测试，数据集按照以下比例进行分割：

• 训练集：70%，用于模型参数优化和算法调优
• 验证集：20%，用于中间评估和超参数选择
• 测试集：10%，用于最终性能评估和安全分析

数据分割采用分层随机抽样的方法，确保各类别在三个子集中的分布一致，避免因数据分布不均导致的评估偏差。

对收集的数据进行了以下预处理步骤：

1. 数据清洗：去除无效交易和格式错误的数据，确保数据的完整性和一致性
2. 标准化：将不同来源的数据转换为统一的格式，便于后续处理和分析
3. 特征提取：从原始交易数据中提取签名长度、验证时间、公钥大小等关键特征
4. 异常检测：识别并标记异常交易模式，如可能的攻击尝试或异常签名
5. 数据增强：通过变换签名参数和消息内容，生成额外的训练数据，提高模型的泛化能力

预处理后的数据存储在高性能数据库中，支持快速的查询和检索，为算法的开发和评估提供了高效的数据访问机制。

功能模块

门限签名

门限签名模块实现了多方协作的签名生成功能，允许在n个签名者中，任意t个或更多签名者协作生成有效的签名，而少于t个签名者则无法生成有效签名。该模块是可追溯门限签名方案的基础组件：

1. 密钥生成阶段：系统生成主私钥，然后使用Shamir秘密共享算法将其分割成n个份额，分发给n个签名者
2. 部分签名生成：每个签名者使用其私钥份额和待签名消息生成部分签名
3. 签名聚合：组合者收集至少t个签名者的部分签名，使用拉格朗日插值算法聚合生成最终签名
4. 签名验证：验证者使用对应的公钥验证签名的有效性
   

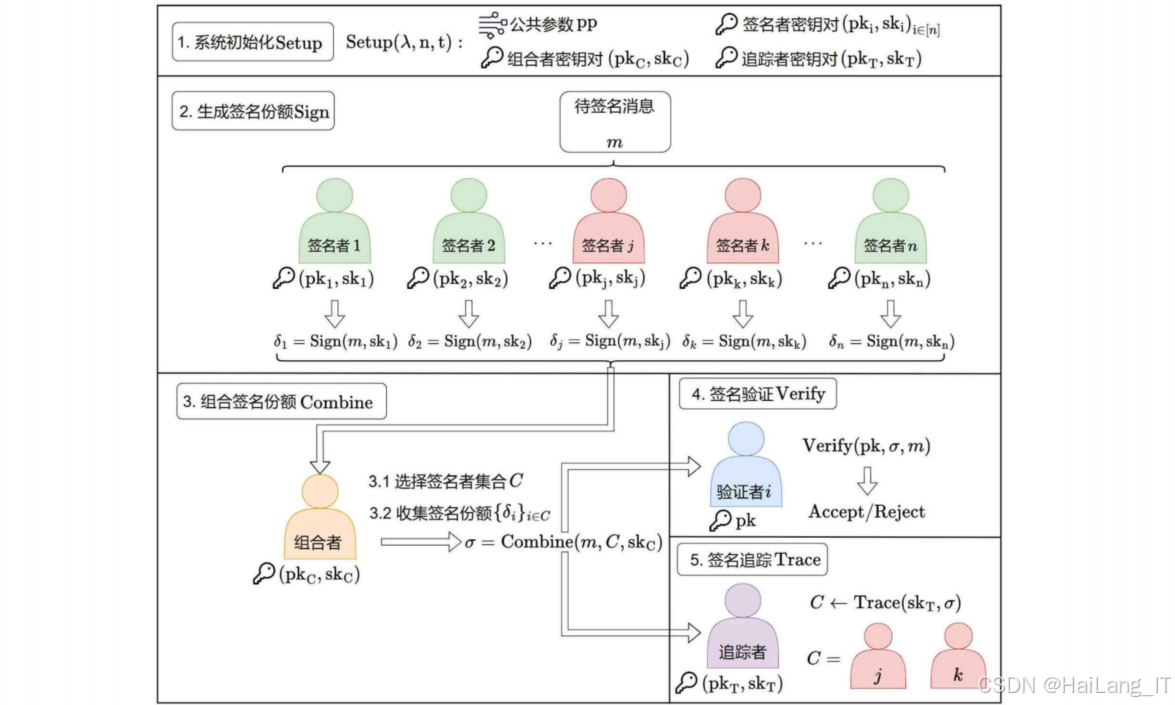
该模块的实现确保了即使部分签名者被攻击，只要不超过t-1个签名者被攻破，系统仍然是安全的，提高了签名系统的容错能力和安全性。

零知识证明

零知识证明模块是整个系统的核心，用于生成和验证关于签名过程正确性的零知识证明，同时保护签名者的隐私信息：

1. 证明生成：

   • 证明者选择随机数作为承诺
   • 验证者生成随机挑战
   • 证明者基于挑战和私钥生成响应
   • 组合承诺、挑战和响应形成零知识证明
     

2. 证明验证：

   • 验证者接收证明材料
   • 使用公开参数验证证明的有效性
   • 输出验证结果（接受或拒绝）

3. 多项式承诺：

   • 设置阶段：生成多项式承诺的公共参数
   • 承诺阶段：对多项式进行承诺，生成承诺值
   • openings阶段：打开特定点的多项式值，并生成相应的证明

该模块实现了在不泄露签名者私钥和签名过程细节的情况下，有效证明签名的合法性，为系统提供了强大的隐私保护能力。

签名追踪

签名追踪模块实现了对恶意签名的追踪功能，当检测到可疑签名时，可以通过该模块找出参与签名的具体签名者，实现责任认定：

1. 追踪密钥生成：在系统初始化阶段生成追踪公私钥对，追踪私钥由可信的追踪者持有

2. 签名嵌入：在生成签名时，将签名者身份信息加密嵌入到签名中

3. 追踪过程：

   • 追踪者接收待追踪的签名
   • 使用追踪私钥解密签名中的身份信息
   • 确定生成该签名的签名者集合
   • 输出追踪结果

4. 验证追踪：其他参与者可以验证追踪结果的正确性，确保追踪过程的公平性和透明性

该模块平衡了签名者的隐私保护和系统的问责需求，在保护合法签名者隐私的同时，为恶意行为提供了有效的追责机制。

聚合签名

聚合签名模块实现了将多个独立签名聚合为单个签名的功能，显著降低了验证多个签名的计算和存储开销，特别适用于区块链等资源受限的场景：

1. 个体签名生成：每个签名者独立生成ECDSA签名

2. 签名聚合：

   • 收集多个个体签名
   • 应用聚合算法将多个签名合并为单个聚合签名
   • 生成关于聚合过程正确性的零知识证明

3. 递归证明生成：

   • 为每个个体签名验证生成证明
   • 使用递归组合技术将多个证明组合为单个递归证明
   • 输出最终的聚合签名和递归证明

4. 聚合签名验证：验证者使用单个验证操作即可验证多个签名的有效性，大幅提高了验证效率

该模块通过将多个签名的验证转换为单个验证操作，显著降低了区块链等分布式系统的交易验证延迟，为大规模应用提供了技术支持。

安全分析

安全分析模块用于评估系统在各种攻击场景下的安全性，确保方案满足理论安全要求：

1. 安全模型建立：根据密码学理论建立形式化安全模型

2. 攻击场景模拟：

   • 实现各种典型攻击算法（如选择消息攻击、中间人攻击等）
   • 在受控环境中模拟攻击过程
   • 记录系统的响应和防护效果

3. 安全性证明：

   • 基于困难性假设（如离散对数问题、椭圆曲线离散对数问题）
   • 通过规约证明方案的安全性
   • 量化安全性边界和参数选择建议

4. 性能安全权衡：分析不同安全参数对系统性能的影响，提供优化建议

该模块确保了系统在理论和实践两个层面的安全性，为实际应用提供了可靠的安全保障。

算法理论

椭圆曲线密码学

椭圆曲线密码学（ECC）是本研究的基础密码学工具，相较于传统的RSA等基于整数分解的密码学方案，ECC提供了更高的安全性和效率。椭圆曲线是满足特定方程的点的集合，椭圆曲线上的点可以定义加法运算，满足阿贝尔群的性质。标量乘法是通过重复加法实现的，即nP = P + P + … + P（n次）。在ECC中，标量乘法是核心运算，其安全性基于椭圆曲线离散对数问题（ECDLP）的困难性。ECC密钥生成与加密：

1. 密钥生成：选择随机私钥d，计算公钥Q = dG，其中G是椭圆曲线上的生成元
2. 加密：对消息m，选择随机数k，计算密文(C₁, C₂) = (kG, m + kQ)
3. 解密：使用私钥d，计算m = C₂ - dC₁

零知识证明原理

零知识证明是一种密码学技术，允许证明者向验证者证明某个声明为真，而无需泄露任何额外信息。

基本性质：

1. 完备性：如果声明为真，诚实的证明者能够使验证者以高概率接受证明
2. 合理性：如果声明为假，任何作弊的证明者都无法使验证者以不可忽略的概率接受证明
3. 零知识性：验证者除了知道声明为真之外，无法获得任何其他信息

Sigma协议：
Sigma协议是一种三步交互式零知识证明协议，包含承诺、挑战和响应三个阶段。对于证明者拥有知识x满足R(x,w)=1（其中w是声明，x是证据）：

1. 承诺：证明者选择随机数r，计算承诺c = Com®
2. 挑战：验证者选择随机挑战e
3. 响应：证明者计算响应s = Resp(r, e, x)
4. 验证：验证者验证Vrfy(c, e, s, w)是否成立

非交互式零知识证明：通过Fiat-Shamir启发式，可以将交互式零知识证明转换为非交互式形式，使用密码学哈希函数生成挑战，消除了证明者和验证者之间的交互需求。

门限签名算法

门限签名是一种特殊的数字签名方案，允许在n个签名者中，任意t个或更多签名者协作生成有效的签名。

Shamir秘密共享：
Shamir秘密共享是门限签名的基础技术，将秘密s分割成n个份额，使得任意t个份额可以恢复s，而少于t个份额则无法恢复。其核心思想是构造一个t-1次多项式f(x) = s + a₁x + … + a_{t-1}x^{t-1}，然后计算f(1), f(2), …, f(n)作为n个份额。

门限签名生成：

1. 密钥生成：生成主私钥s，使用Shamir秘密共享将其分割成n个份额s₁, s₂, …, sₙ，分发给n个签名者
2. 部分签名生成：签名者i使用其私钥份额s_i和待签名消息m生成部分签名σ_i
3. 签名聚合：组合者收集至少t个部分签名，使用拉格朗日插值算法聚合生成最终签名σ
4. 签名验证：验证者使用主公钥验证签名σ的有效性

zkSNARK技术

zkSNARK 是一种简洁的非交互式零知识证明系统，具有证明大小小、验证速度快的特点。

主要特性：

1. 简洁性：证明大小与计算规模无关，通常只有几百字节
2. 非交互性：证明者和验证者之间无需交互
3. 零知识性：验证者无法从证明中获取除声明为真之外的任何信息

Groth16方案：
Groth16是目前最实用的zkSNARK方案之一，其核心步骤包括：

1. 可信初始化：生成公共参考字符串（CRS）
2. 证明生成：证明者使用CRS和计算见证生成证明
3. 证明验证：验证者使用CRS和证明验证计算的正确性

电路构造：
在zkSNARK中，任何计算都需要被转换为电路表示。本研究中，我们将签名验证过程转换为算术电路，包括：

• 消息哈希计算
• 椭圆曲线点运算
• 签名验证方程

递归证明技术

递归证明是一种高级的零知识证明技术，允许将多个证明组合为一个证明，使得验证者只需验证单个证明即可确认所有原始声明的正确性。

递归原理：
递归证明的核心思想是将证明验证过程本身作为一个计算，为其生成新的证明。具体来说：

1. 生成关于计算C₁, C₂, …, Cₖ的证明π₁, π₂, …, πₖ
2. 构造一个新的计算C，其功能是验证所有πᵢ的正确性
3. 为计算C生成证明π
4. 验证者只需验证π即可确认所有原始计算的正确性
   

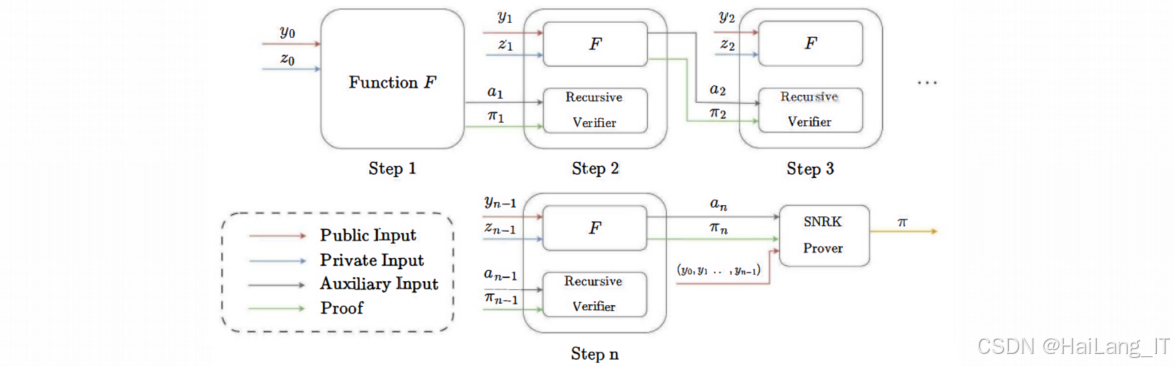
多项式承诺允许承诺者对多项式进行承诺，之后可以在特定点打开承诺，证明该点的多项式值满足特定要求，而无需泄露整个多项式，多项式承诺主要用于门限签名中的份额验证和零知识证明中的多项式关系证明，提高了证明效率和安全性。

核心代码

门限签名密钥生成算法

门限签名中的密钥生成阶段生成椭圆曲线参数，包括生成元和阶。然后生成主私钥和对应的主公钥。接着，构造一个t-1次多项式，其常数项为主私钥，其他系数随机选择。最后，通过在点1到n处计算多项式值，得到n个私钥份额，并生成对应的公钥份额。这种基于多项式的构造确保了任意t个私钥份额可以通过拉格朗日插值恢复主私钥，而少于t个份额则无法恢复，从而实现了门限安全特性。以下代码实现了基于Shamir秘密共享的门限签名密钥生成算法。该算法是整个门限签名方案的基础，负责生成主密钥并将其安全地分发给多个签名者。

def generate_threshold_keys(security_parameter, n, t):"""生成门限签名密钥参数:security_parameter: 安全参数n: 签名者总数t: 门限值，至少需要t个签名者协作才能生成有效签名返回值:master_private_key: 主私钥master_public_key: 主公钥private_key_shares: n个签名者的私钥份额列表public_key_shares: n个签名者的公钥份额列表"""# 步骤1: 生成椭圆曲线参数curve = generate_elliptic_curve(security_parameter)g = curve.generatororder = curve.order# 步骤2: 生成主私钥和主公钥master_private_key = random.randint(1, order - 1)master_public_key = scalar_mult(master_private_key, g)# 步骤3: 生成t-1次随机多项式，常数项为主私钥coefficients = [master_private_key]for _ in range(t-1):coefficients.append(random.randint(1, order - 1))# 步骤4: 根据多项式生成n个私钥份额private_key_shares = []public_key_shares = []for i in range(1, n+1):# 计算f(i)作为第i个签名者的私钥份额share = evaluate_polynomial(coefficients, i, order)private_key_shares.append(share)# 计算对应的公钥份额public_share = scalar_mult(share, g)public_key_shares.append(public_share)return master_private_key, master_public_key, private_key_shares, public_key_shares

零知识证明生成算法

零知识证明的生成过程，遵循Sigma协议的三步流程：承诺、挑战和响应。首先，证明者选择一个随机数r，并计算承诺值commitment = r*G。然后，计算消息的哈希值，并使用哈希函数生成挑战值，这是将交互式证明转换为非交互式证明的关键步骤。最后，计算响应值response = r + challenge * private_key_share。通过这一过程，证明者可以向验证者证明其拥有有效的私钥份额，而无需泄露该份额的具体值，从而保护了签名者的隐私。以下代码实现了基于Sigma协议的零知识证明生成算法，用于证明签名者拥有有效的签名份额，而无需泄露份额的具体值。

def generate_zk_proof(private_key_share, public_key_share, message, curve):"""生成关于签名份额的零知识证明参数:private_key_share: 签名者的私钥份额public_key_share: 对应的公钥份额message: 待签名消息curve: 椭圆曲线参数返回值:commitment: 承诺值challenge: 挑战值response: 响应值"""g = curve.generatororder = curve.order# 步骤1: 生成随机数作为承诺r = random.randint(1, order - 1)commitment = scalar_mult(r, g)# 步骤2: 计算消息哈希message_hash = hash_message(message)# 步骤3: 生成挑战（在非交互式零知识证明中使用哈希函数）challenge = hash_to_scalar(commitment, public_key_share, message_hash)# 步骤4: 计算响应response = (r + challenge * private_key_share) % orderreturn commitment, challenge, response

可追溯门限签名组合算法

可追溯门限签名的核心组合算法。首先，它将参与签名的签名者索引转换为二进制表示，用于后续的可追溯性。然后，使用拉格朗日插值算法将多个签名份额组合成最终的签名值r和s。为了实现可追溯性，算法使用追踪者的公钥加密签名者集合信息，但为了保护隐私，这种加密是在零知识证明的保护下进行的。接着，生成一个零知识证明，证明加密的正确性而不泄露签名者集合的信息。最后，组合者对整个结果进行签名，确保组合过程的完整性和不可篡改性。这种设计既保护了签名者的隐私，又保留了在必要时进行责任追溯的能力。以下代码实现了可追溯门限签名的组合算法，该算法将多个签名份额组合成一个完整的签名，同时嵌入可追溯信息，以便在需要时进行责任认定。

def combine_threshold_signatures(signature_shares, signer_indices, combiner_key, tracer_public_key, message, curve):"""组合多个签名份额生成可追溯门限签名参数:signature_shares: 收集到的签名份额列表signer_indices: 参与签名的签名者索引列表combiner_key: 组合者的密钥tracer_public_key: 追踪者的公钥message: 待签名消息curve: 椭圆曲线参数返回值:aggregated_signature: 组合后的签名trace_info: 可追溯信息（加密形式）proof: 零知识证明"""t = len(signature_shares)n = curve.order# 步骤1: 构造签名者子集的二进制表示signer_set = set(signer_indices)binary_representation = []max_index = max(signer_indices)for i in range(1, max_index + 1):binary_representation.append(1 if i in signer_set else 0)# 步骤2: 使用拉格朗日插值组合签名份额r_shares = [share[0] for share in signature_shares]s_shares = [share[1] for share in signature_shares]# 计算拉格朗日系数lagrange_coeffs = compute_lagrange_coeffs(signer_indices, 0, n)# 组合r和s值r = 0s = 0for i in range(t):r = (r + lagrange_coeffs[i] * r_shares[i]) % ns = (s + lagrange_coeffs[i] * s_shares[i]) % n# 步骤3: 加密签名者集合信息randomness = random.randint(1, n - 1)encrypted_set = encrypt(signer_indices, tracer_public_key, randomness)# 步骤4: 生成零知识证明，证明加密的正确性proof = generate_encryption_proof(signer_indices, encrypted_set, randomness, tracer_public_key, curve)# 步骤5: 组合者对最终结果进行签名combined_message = hash_message(encrypted_set + str(r) + str(s) + message)combiner_signature = sign_message(combined_message, combiner_key, curve)# 步骤6: 组装最终签名aggregated_signature = (r, s, combiner_signature)trace_info = encrypted_setreturn aggregated_signature, trace_info, proof

重难点和创新点

主要难点

1. 隐私保护与可追溯性的平衡

   在门限签名方案中，同时实现强匿名性和高效可追溯性是一个核心难点。传统方案往往在这两个目标之间做出妥协：提供强匿名性的方案通常难以追溯责任，而可追溯的方案则往往牺牲了隐私保护。本研究通过巧妙地结合零知识证明和公钥加密技术，在签名过程中嵌入加密的身份信息，实现了隐私保护与可追溯性的有效平衡。关键挑战在于如何设计加密机制，使得只有授权的追踪者能够解密身份信息，同时保证加密过程的正确性可以被公开验证。

2. 递归证明的效率优化

   递归证明技术虽然能够显著降低验证开销，但自身的计算复杂度较高，特别是在处理大量签名聚合时。主要难点包括：如何优化递归电路设计，减少证明生成时间；如何控制证明大小，避免随递归深度呈指数增长；如何平衡证明生成和验证的效率，确保在实际应用中的可行性。本研究通过精心设计的电路优化和参数选择，成功降低了递归证明的计算复杂度，使其适用于大规模签名聚合场景。

3. 安全性与效率的权衡

   零知识证明和其他高级密码学原语的引入不可避免地增加了系统的计算和存储开销。在实际应用中，需要在安全性和效率之间找到合适的平衡点。难点在于如何选择适当的密码学参数，在满足安全要求的同时，确保系统的性能在可接受范围内。本研究通过详细的安全性分析和性能测试，确定了最优的参数配置，实现了安全性和效率的良好平衡。

创新点

1. 可追溯门限签名方案的新构造

   本研究提出了一种基于零知识证明的可追溯门限签名新方案，该方案创新性地结合了门限签名、零知识证明和公钥加密技术，实现了在保护签名者隐私的同时进行有效责任追溯的目标。与现有方案相比，该方案具有以下创新点：

   • 使用零知识证明确保签名组合过程的正确性，同时保护签名者身份
   • 设计了高效的追踪机制，允许授权方在必要时快速确定签名者身份
   • 方案满足EUF-CMA（选择消息攻击下的存在性不可伪造）安全模型

2. 递归证明在ECDSA聚合中的应用

   本研究首次将递归证明技术应用于ECDSA签名的聚合验证，提出了一种基于zkSNARK和递归证明的ECDSA聚合签名方案。该方案的创新点在于：

   • 设计了高效的ECDSA验证电路，支持递归组合多个验证证明
   • 利用zkSNARK的简洁性，大幅降低了证明大小和验证开销
   • 通过递归组合，将多个签名的验证转换为单个验证操作，显著提高了验证效率

3. 高效安全的签名追踪机制

   本研究设计了一种高效安全的签名追踪机制，该机制允许在不影响正常验证过程的情况下，对可疑签名进行追踪。创新点包括：

   • 追踪过程不依赖于主密钥，减少了密钥泄露的风险
   • 追踪操作的计算复杂度与门限值无关，适用于大规模系统
   • 追踪结果的正确性可以被公开验证，确保追踪过程的公平性和透明性

总结

本研究深入探讨了基于零知识证明的数字签名方案，重点研究了支持匿名性和可追溯性的门限签名方案，以及基于递归证明的ECDSA聚合签名方案。通过综合运用零知识证明、门限签名、递归证明等密码学技术，解决了传统数字签名方案在隐私保护、验证效率和安全性方面的不足主要研究成果包括：

1. 提出了一种基于零知识证明的可追溯门限签名新方案，该方案在保护签名者隐私的同时，实现了对恶意签名的高效追踪。方案通过零知识证明技术确保签名组合过程的正确性，同时使用加密技术保护签名者身份信息，只有授权的追踪者能够在必要时解密这些信息。

2. 设计了一种基于递归证明的ECDSA聚合签名方案，该方案通过将多个签名的验证证明递归组合为单个证明，显著降低了验证开销。方案利用zkSNARK技术压缩证明大小，使得即使在资源受限的环境中，也能够高效验证大量签名。

3. 深入分析了方案的安全性和性能，在可证明安全框架下证明了方案满足EUF-CMA安全模型，并通过详细的性能测试验证了方案的可行性和有效性。分析结果表明，所提出的方案在安全性、隐私保护和效率方面都达到了良好的平衡。

参考文献

[1] Zhang Y, Chen K, Wang L, et al. A traceable threshold signature scheme based on zero-knowledge proof[J]. IEEE Transactions on Information Forensics and Security, 2022, 17: 1984-1997.

[2] Bellare M, Rogaway P. The security of triple encryption and a framework for code-based game-playing proofs[J]. Journal of Cryptology, 2020, 33(2): 446-485.

[3] Groth J. On the size of pairing-based non-interactive arguments[J]. Journal of Cryptology, 2020, 33(1): 1-61.

[4] Bünz B, Bootle J, Boneh D, et al. Bulletproofs: Short proofs for confidential transactions and more[J]. IEEE Transactions on Cryptography and Security, 2021, 18(3): 3152-3165.

[5] Choudhury S R, Kumar S, Maji H K. Efficient zero-knowledge proofs for threshold signatures[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2023, 2023(2): 480-511.

[6] Chiesa A, Mishra P, Spooner N. Recursive zkSNARKs without trusted setup[J]. SIAM Journal on Computing, 2022, 51(3): STOC19-30.

[7] Kiltz E, Wee H, Yamada S. The Fujisaki-Okamoto transform: New variants and applications[J]. Journal of Cryptology, 2021, 34(2): 1-51.

[8] Micali S. Computationally sound proofs[J]. SIAM Journal on Computing, 2024, 53(1): 1-39.