机器学习日报14

摘要

今天学习了决策树集成方法，特别是随机森林算法。单个决策树对数据微小变化很敏感，通过构建多个决策树并让它们投票可以提高预测的稳定性和准确性。放回抽样技术是构建树集成的关键，它能创建多个相似但不同的训练集。随机森林通过有放回抽样生成B个训练集，在每个节点随机选择特征子集进行分裂，最终通过投票得出预测结果。

Abstract

Today’s lesson covered decision tree ensembles, focusing on the random forest algorithm. Single decision trees are sensitive to small data variations, but building multiple trees and having them vote improves stability and accuracy. The key technique is sampling with replacement, which creates multiple similar but distinct training sets. Random forest generates B training sets through sampling, randomly selects feature subsets at each node for splitting, and makes predictions through voting.

一、使用多个决策树

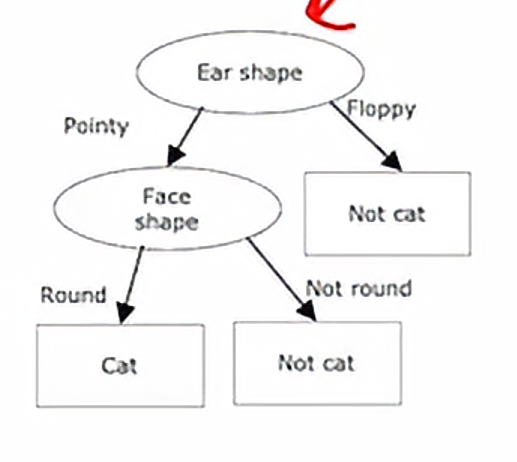
使用单个决策树的一个缺点是，它可能对微小的变化有很高的敏感度，要使算法变得不那么敏感的话，一个更稳健的解决方案是建造不止一个决策树，而是建造大量的决策树，我们一般称之为树集成，我们继续用我们之前经常提到的那个例子，就是我们将根节点设置为耳朵形状，然后我们将样本分例，然后我们再在这两个数据子集上进一步构建子树

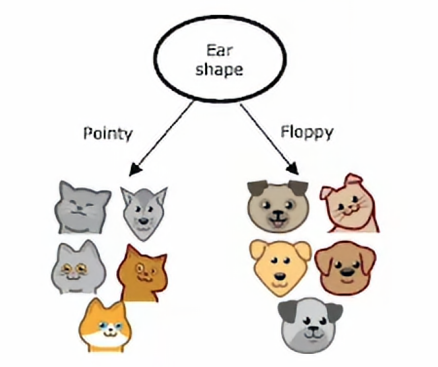
假如我们进行一下小改动

就是将左边画圆圈的猫，左猫是尖耳朵、圆脸、没有胡须，我们改变成垂耳、圆脸、有胡须，那么这样右边的信息增益最高的分割特征就会变成胡须特征而不是耳朵形状特征，因此，我们在左右子树得到的数据子集会完全不同，并且当我们继续递归运行决策树学习算法时，我们会在左右构建出完全不同的子树，所以改变一个训练样本就能导致算法在根节点进行不同的分割，这使得这个算法不是那么稳健，这就是为什么我们在使用决策树时，我们通常会得到更好的结果，也就是说，如果我不仅训练单个决策树，而是训练一大堆决策树，我们会得到更准确的预测

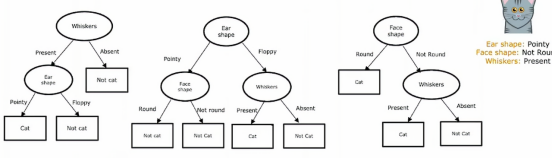
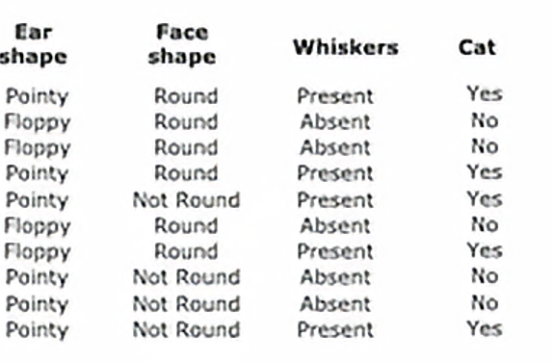
这就是我们所说的树集成，意思就是多个树的集合，在之后的学习中，我们将看到如何构建这个集成树，但是我们有三个树的集成，每一个都是一种合理区分猫和非猫的方法，如果有一个新的测试样本需要分类，我们要做的是在这个新样本上运行这三棵树，并让它们对最终预测进行投票，比如这个测试样本有尖尖的耳朵，不是圆形的脸型、有胡须，所以第一个树会是这样的推断，先是有胡须，往左走，然后尖耳朵往左走，走到叶节点判定为猫，第二棵树首先是尖耳朵，往左走，然后不是圆脸往右走，这棵树判定为非猫，然后我们看第三个，首先看脸型，脸型不是圆形往右走，然后判定胡须，是有胡须的，所以我们往左走，第三棵树判定的结果是猫，这三棵树预测的结果不同，所以我们实际上会为它们投票，这三棵树预测结果多数都是预测为猫，所以综合三棵树的结果，最终判断为该动物为猫

所以我们使用树集成的原因是由于拥有大量的决策树，这使得整体算法对任何单棵树的影响变得不那么敏感，因为预测错的情况三票中只占一票，当然我们现实情况下肯定是不止三颗的，可能成千上百棵，我们只需要统计所有树的结果，然后看哪个结果占大多数，我们最终就预测为哪个结果

现在我们知道为什么要使用树集成了，但是树集成的原理我们还不知道，我们该写出一个怎样的算法来得出这些不同的解释呢，我们又如何为每个树进行投票最终得出结果呢，这就引出了我们下一个小节的核心–放回抽样

二、放回抽样

为了构建一个树集成模型，我们需要一个叫做放回抽样的技术

为了说明放回采样如何工作，将演示如何使用放回采样，使用四个颜色的标记，分别为红色、黄色、绿色、蓝色

现在假设我们将四个样本放进一个黑箱子里，我们从外面是完全看不到里面是什么样子，然后我们将黑箱子摇匀，我们就可以从箱子里面抽取样本，有放回的意思是，在我们抽取了一样本之后抽取下一个样本之前，我们需要将刚抽取的样本放回，然后摇匀之后，再抽取，现在我们抽取多次的结果如下：

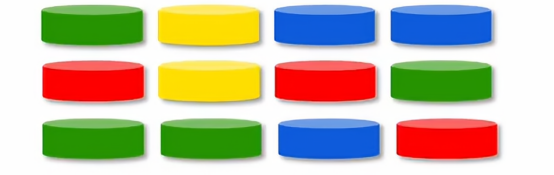
注意，有放回抽样这一点非常关键，因为如果我们每次抽样后不把标记放回，那么如果我们从我们的四个标记袋中抽出四个标记，我们总是会抽到四个相同的标记，这就是为什么我们每次抽取后都要放回样本，这样以至于我们不会抽到相同的四个

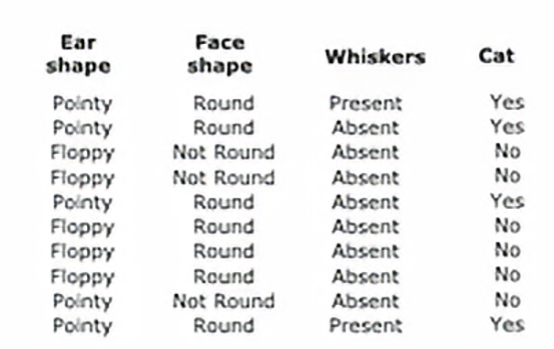
有放回抽样在构建树的集成方法中的应用如下，我们将构建多个随机训练集，这些训练集与原始训练集略有不同，特别是，我们将采用我们的10个猫和狗的例子，我们将这10个训练例子放入一个假想的袋子中，利用这个假想的袋子，我们将创建一个新的随机训练集，由10个与原始数据集大小相同的例子组成，我们随机拿出几个训练例子，构成如下的表

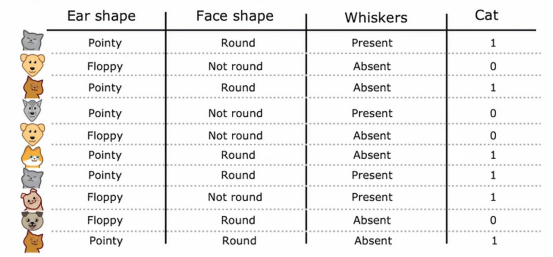
我们会注意到，这10个例子中有些例子是重复的，并且这10个例子并没有显示出完整的训练集，这样看来放回抽样的过程让我们构造一个有点类似于新的训练集，但是又有很大的不同，事实证明，这将是构建树集成的关键构建

三、随机森林算法

既然我们已经有了一个使用放回抽样来创建新的训练集的方法，这些训练集既有点类似，但也与原始训练集大不相同，我们已经准备好构建我们第一个集成树算法了，特别是我们会讨论一下随机森林算法，随机森林算法是一种强大的树集成算法，比使用单个决策树效果要好很多

假设我们有一个大小为m的训练集，然后对于b=1到B，所以我们执行这大写B次，我们可以使用有放回抽样来创建一个大小为m的新训练集，假设我们有10个训练样本

那么我们将会把这10个训练样本放在那个虚拟的袋子里，并进行10次有放回抽样以生成一个新的训练集，也是10个样本，然后我们会在这个训练集上训练一个决策树，所以这是我们使用有放回抽样生成的数据集，我们可能会注意到有些训练样本是会重复的，如果我们在这个数据集上训练决策算法，那么我们最终会得到这个决策树

完成一次之后，我们会重复第二次，使用放回抽样生成的另外包含m或10个训练样本的训练集


然后我们在这个新训练集上训练决策树，我们可能总共这样做B次，我们构建树的数量，可能在100次左右，我们从推荐的值从，比如，64到128，构建了一个集成模型后，比如一百棵不同的树，然后我们尝试进行预测时，让这些树都投票决定正确的最终预测结果，事实证明，设定更大的B并不会影响性能，我们最终会面临收益递减，而且当B远大于这个数值时，实际效果并不会有明显提升，大概100左右，那只会显著减慢计算速度，并不会显著提升整体性能，这种集成树的构成我们也叫袋装决策树，这指的是将我们的训练示例放入那个虚拟袋中，这也是我们在这里使用小写b和大写B的原因，对这个算法有一个改进版，实际上会使其表现的更好，关键思想是即使使用这种有放回抽样的程序，有时我们最终总在根节点上使用相同的分裂，以及在根节点附近进行非常相似的分裂，在上面这个例子中，训练集的小变化导致了根节点处的不同分裂，但是很多例子都是在根节点处选择相似的分裂，所以对这个算法有一种修改，可以进一步尝试在每个节点随机化特征选择，可能会导致我们学到的树集合变得更加不同，我们最终会得到更加准确的预测，所以通常的做法是，在每个节点选择特征进行分裂时，如果有n个特征可用，在我们的例子中我们有三个特征，而不是从所有特征中选择，并允许算法仅从这个k个特征子集中选择，换句话说，我们会选择k个特征作为允许的特征，选择信息增益最高的特征作为分裂用的特征，当n很大的时候，k的一个典型选择就是n的平方根，这种技术往往更多用于具有大量特征的更大问题

通过对这个算法进一步的修改，它通常会工作得更好，而且比单个决策树要稳健得多，其中得原因之一是替换采样过程已经导致算法探索了数据的许多小变化，并且平均所有这些由替换采样过程引起的数据变化，这意味着对训练集的任何小的进一步改动，都不太可能对整体随机森林算法的输出产生过大的影响，因为它已经探索并平均了训练集的许多小变化

总结

今天的学习让我明白了为什么单个决策树不够稳健，以及如何通过集成方法解决这个问题。随机森林的核心思想很巧妙——通过有放回抽样创造多个略有差异的训练集，然后在每个节点随机选择特征，这样每棵树都变得独特。最后通过投票机制，即使某棵树预测错误，整体结果仍然可靠。这种"三个臭皮匠顶个诸葛亮"的思路确实能显著提升模型性能。放回抽样的过程让我想到了抽奖游戏，每次抽完放回确保每次抽取都是独立的。随机森林相比单棵决策树确实更适合实际应用。