当前位置： 首页 > news >正文

破解EEG逆问题：ADMM-ESINet如何融合优化理论与深度学习实现实时源成像

news 2025/11/8 9:05:13

论文信息

  • 标题：ADMM-ESINet: A Deep Unrolling Network for EEG Extended Source Imaging

  • 作者：Ke Liu, Hang Jiang, Hu Yang, Jun Zhang, Zhenghui Gu, Zhuliang Yu, Yu Zhang, Bin Xiao, Wei Wu

  • 期刊：IEEE Journal of Biomedical and Health Informatics

  • 卷期：Vol. 29, No. 10, October 2025

  • DOI：10.1109/JBHI.2025.3568648

  • 开源代码：https://github.com/hangj-cache/ADMM-ESINet

论文主要贡献

  1. 提出ADMM-ESINet：一种基于算法展开的深度神经网络，将ADMM迭代过程转化为网络层，融合了先验知识，提高了泛化能力和可解释性。

  2. 实时性能提升：相比传统模型驱动方法，ADMM-ESINet能在毫秒级内完成源重建，适用于实时应用。

  3. 参数效率高：网络参数较少，比传统深度学习方法更轻量，且泛化能力更强。

  4. 自适应学习：正则化参数和空间变换算子直接从训练数据中学习，避免了手动调参的困难。

背景解释：EEG源成像的挑战

EEG源成像（ESI）旨在从头皮EEG信号中逆向估计大脑皮层源的活动，这是一个高度病态的逆问题（电极数远少于源数）。传统方法分为：

  • 模型驱动方法：如wMNE和LORETA，使用数学约束（如L2范数），但重建结果扩散且依赖手动调参。

  • 数据驱动方法：基于深度学习，实时性好但泛化能力差。

    ADMM-ESINet通过算法展开技术结合两者优点。

方法详解：深入数学公式与网络架构

本节将详细讲解ADMM-ESINet的数学基础和网络设计，重点解释公式推导和关键步骤。

1. 问题建模与数学基础

EEG源成像的线性模型为：

X=LS+\varepsilon

其中：

  • X\in \mathbb{R}^{N_{c}\times N_{t}}：EEG信号（N_{c}个电极，N_{t}个时间点）。

  • S\in \mathbb{R}^{N_{s}\times N_{t}}​：源信号（N_{s}个源，通常N_{s}≫N_{c}）。

  • L\in \mathbb{R}^{N_{c}\times N_{s}}​：导联场矩阵，通过边界元法（BEM）计算。

  • \varepsilon：测量噪声。

由于病态性，需引入正则化框架估计源：

\hat{S}=arg\underset{S}{min}\frac{1}{2}\left \| X-LS \right \|_{F}^{2}+h(S)

这里，h(S)是正则化项，代表先验约束。ADMM-ESINet使用结构化稀疏约束：

h(S)=\lambda _{1}\left \| VS \right \|_{2,1}+\lambda _{2}\left \| S \right \|_{2,1}

  • \left \| Y \right \|_{2,1}=\sum_{i=1}^{P}\sqrt{\sum_{j=1}^{Q}y_{ij}^{2}}：L_{2,1}范数，促进行稀疏（即源在时间维度上稀疏，但空间上连续）。

  • V：空间变换算子（如拉普拉斯算子），可从数据学习。

  • \lambda _{1},\lambda_{2}：正则化参数，通过训练自适应调整。

为降低计算复杂度，论文使用时间基函数（TBFs）进行降维。对EEG信号X进行奇异值分解（SVD），提取K个TBFs（\phi \in \mathbb{R}^{K\times T}），投影后模型简化为：

\tilde{X}=\tilde{L}\tilde{S}+\tilde{\varepsilon }

其中\tilde{S}=S\phi ^{T}。最终源通过逆映射S=\tilde{S}\phi恢复。

2. ADMM算法推导

ADMM-ESINet的核心是将优化问题转化为ADMM迭代。引入辅助变量Z，将问题重写为约束形式：

\hat{S}=arg\underset{S}{min}\frac{1}{2}\left \| X-LS \right \|_{F}^{2}+\lambda _{1}\left \| VZ \right \|_{2,1}+\lambda _{2}\left \| Z \right \|_{2,1} \; \; s.t. \; \; Z=S

增广拉格朗日函数为：

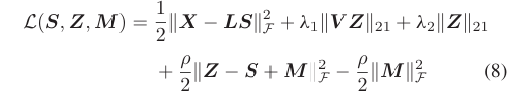
其中M是拉格朗日乘子，ρ>0是惩罚参数。ADMM迭代步骤如下：

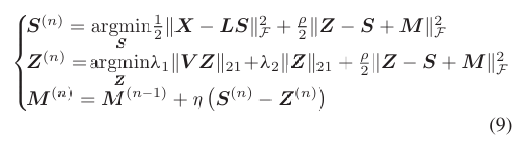
其中\eta是更新率。每个子问题可解析求解或近似。

3. 网络层展开详解

通过算法展开，将ADMM迭代映射为神经网络层。ADMM-ESINet由多个块组成（默认6个），每个块对应一次迭代，包含三层：

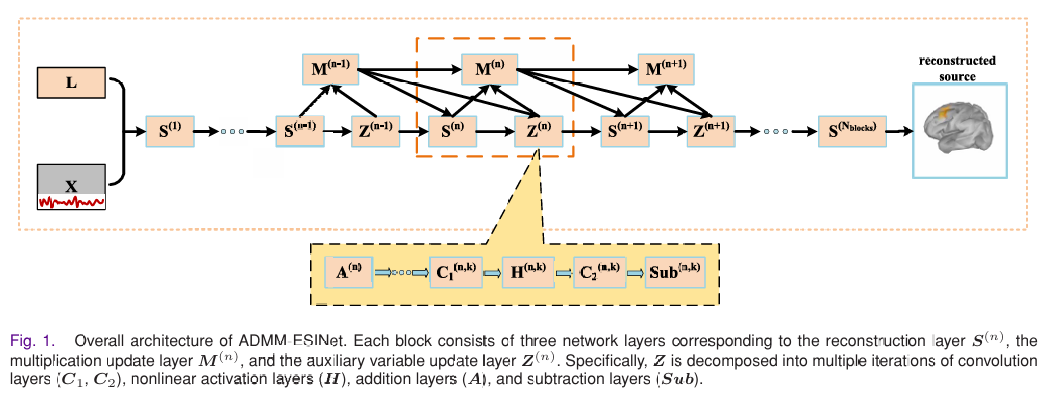
  • 重构层（S(n)）：

    求解S(n)子问题，闭式解为：

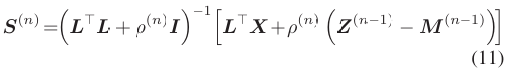
    实践中，ρ作为可学习参数，第一层初始化时Z(0)和M(0)不存在，故：

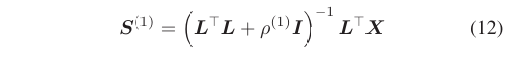
    该层通过矩阵求逆（使用预计算或迭代方法）实现，融合了数据拟合项和约束项。

  • 乘子更新层（M(n)）：

    直接对应ADMM的乘子更新，但引入可学习参数增强灵活性：

    其中\eta _{1}，\eta _{2}，\eta _{3}通过训练优化，替代固定值\eta。

  • 辅助变量层（Z(n)）：

    Z(n)子问题非光滑，通过梯度下降近似。定义梯度步：

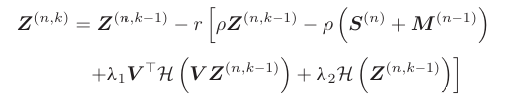
    其中r是步长，H(⋅)是非线性激活函数，对应L_{2,1}范数的次梯度。重写为：

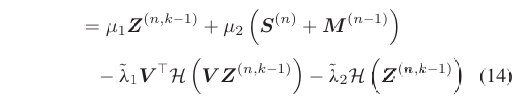
    这里\mu _{1}=1-r\rho, \mu _{2}=r\rho, \tilde{\lambda _{1}}=r\lambda _{1}, \tilde{\lambda _{2}}=r\lambda _{2}​。该层通过卷积模块实现：

  • 卷积模块C1​和C2​：使用卷积核（大小16×1）处理输入，后接激活函数和反卷积。

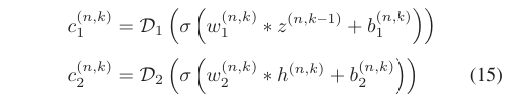
  • 激活层H：实现稀疏约束，公式为：

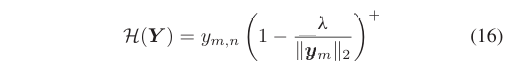
    其中(⋅)+=max(⋅,0)，促进行稀疏。

  • 加法和减法层：组合各分量，最终输出Z(n)=Z(n,Nt​)。

损失函数采用均方误差（MSE）：

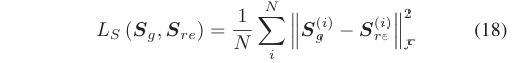
训练使用Adam优化器，学习率衰减策略。

实验设计与结果分析

数值模拟的全面性设计

论文设计了三个层次的验证场景，全面评估方法性能：

单源场景下的系统性测试：

  • 信噪比变化：-5dB到10dB，覆盖实际EEG记录的典型噪声范围

  • 源尺寸变化：5cm²到32cm²，涵盖典型脑功能活动的空间尺度

  • 每种条件100次蒙特卡洛模拟，确保统计显著性

多源场景的挑战性测试：

  • 同侧半球双源：测试空间分辨能力

  • 对侧半球双源：测试全局定位能力

  • 不同源尺寸组合：验证方法的适应性

性能评估指标的科学性

四个指标从不同角度评估性能：

  1. AUC（曲线下面积）：综合评价检测灵敏度与特异性

  2. 空间分散（SD）：量化源估计的空间集中程度

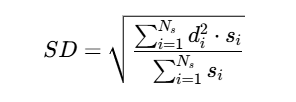
    其中di​为估计源到真实源的距离，s_{i}为源强度

  3. 定位误差（DLE）：评估中心位置的准确性

  4. 相对均方误差（RMSE）：衡量时间过程重建质量

实验结果深度分析

噪声鲁棒性表现：

如图4所示，ADMM-ESINet在低信噪比（-5dB）下仍保持较高性能，AUC值显著高于对比方法（p<0.01）。这种鲁棒性源于结构化稀疏约束对噪声的自然抑制。

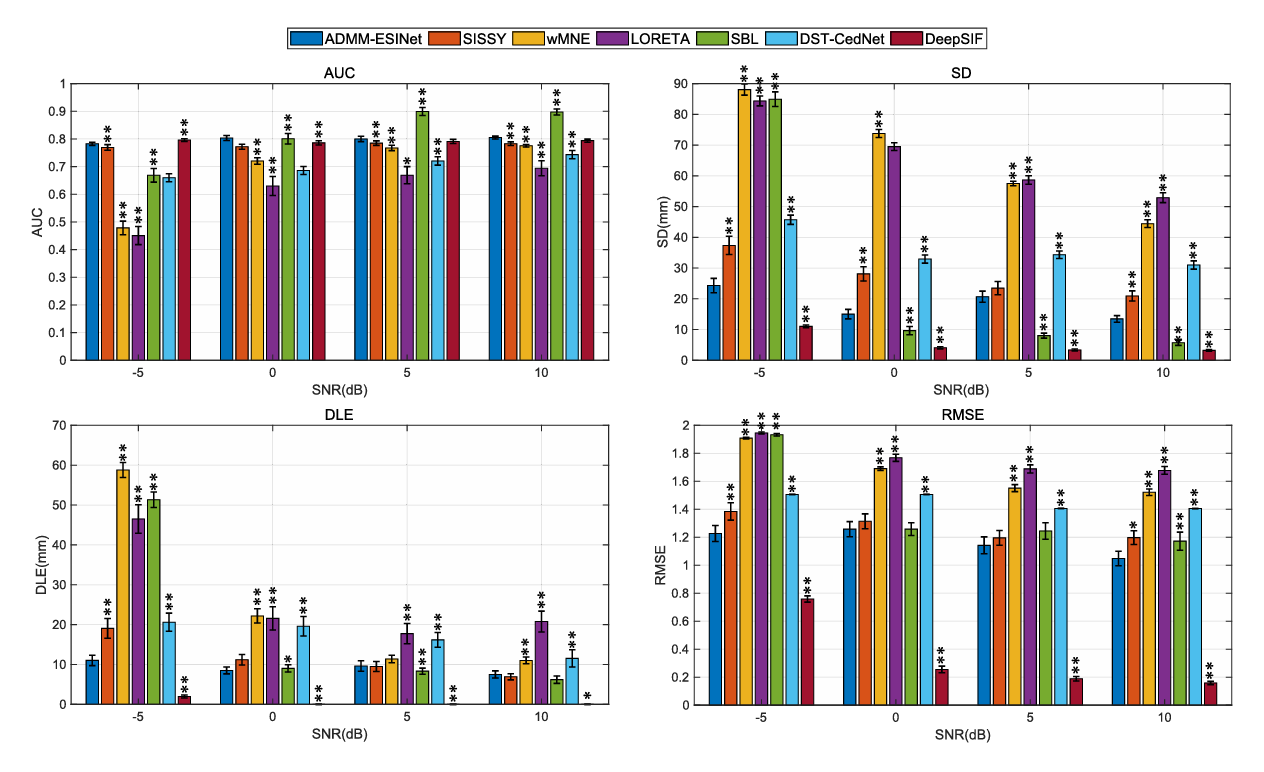
源尺寸适应性分析：

当源尺寸从5cm²增大到32cm²时，ADMM-ESINet的AUC从0.85提升到0.94，表明方法能够有效捕捉不同空间范围的神经活动。相比之下，SBL方法因稀疏假设限制，在大源尺寸下性能下降。

多源分辨能力：

在图8展示的双源场景中，ADMM-ESINet成功分离了两个空间接近的源，而传统方法如wMNE和LORETA出现严重的源混淆现象。

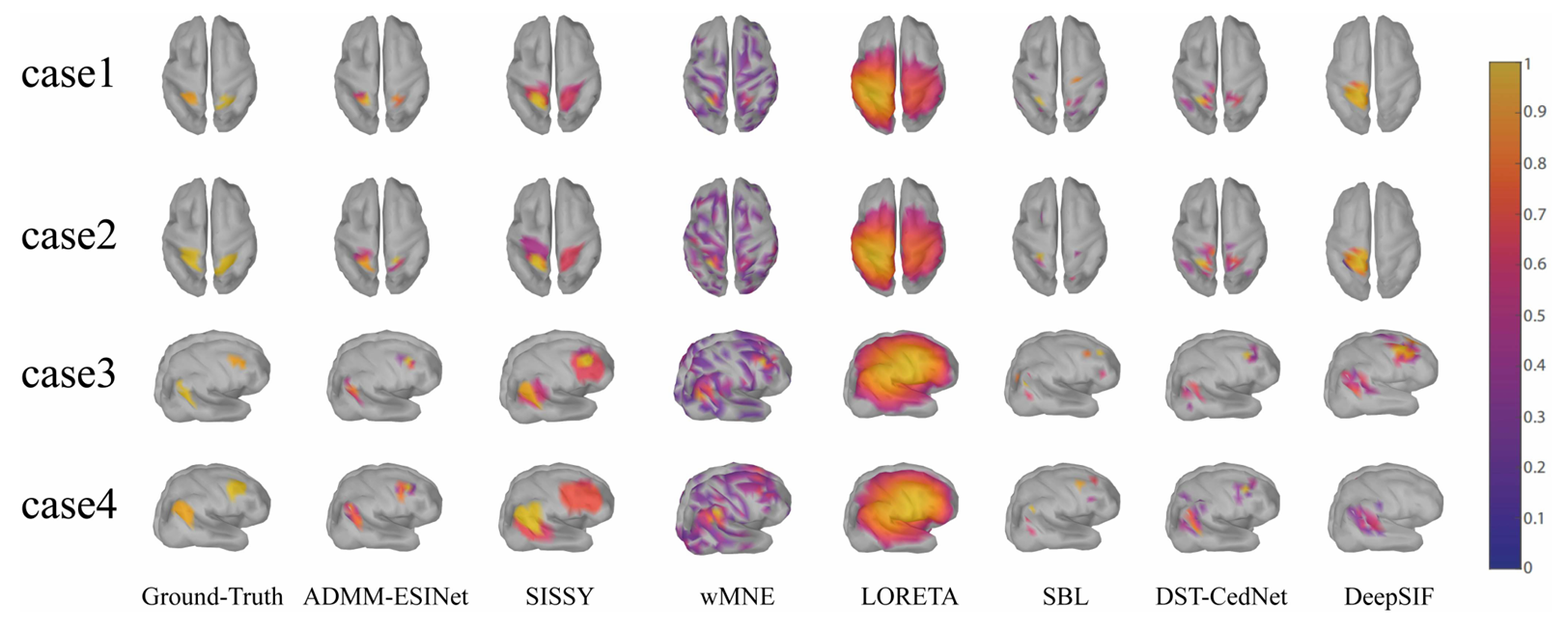
真实数据验证的临床意义

癫痫灶定位精度：

在癫痫患者数据中，ADMM-ESINet准确识别了致痫灶的位置和范围（图9），与手术切除区域高度一致。这一结果具有重要临床价值，因为精确的灶区定位直接影响手术成功率。

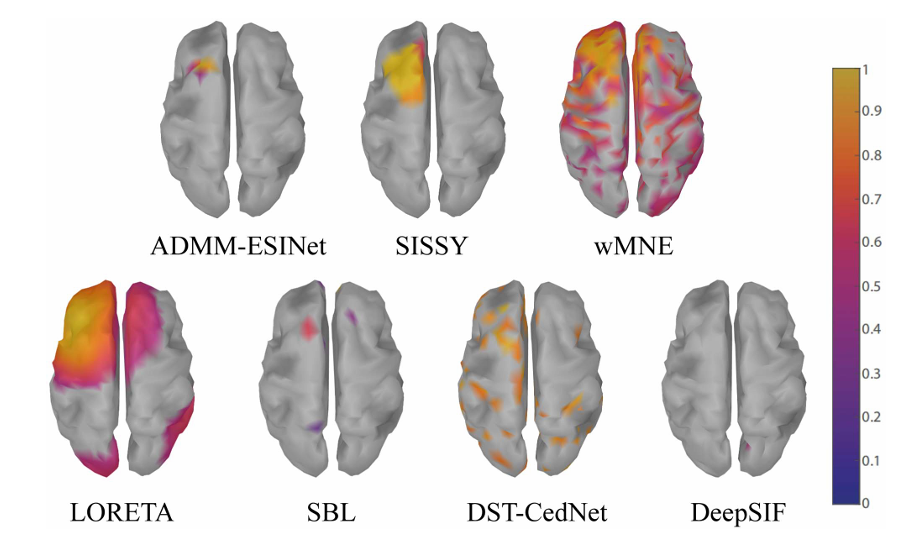
感觉运动皮层的激活映射：

在Yokogawa数据集中，方法成功定位了median神经刺激激活的初级感觉皮层，显示了在正常脑功能研究中的应用潜力。

方法优势的定量比较

计算效率对比

如表II所示，ADMM-ESINet的单试次处理时间为67.6ms，满足实时性要求（通常<100ms）。相比之下，传统迭代方法如SISSY需要1733.2ms，无法满足实时应用需求。

参数效率分析

ADMM-ESINet仅需17934个参数，远少于DeepSIF的2360万参数。这种参数效率不仅减少计算资源需求，还降低了过拟合风险，提高了泛化能力。

泛化能力验证

在从模拟数据到真实数据的迁移测试中，ADMM-ESINet保持了稳定性能，而纯数据驱动方法（如DST-CedNet）出现显著性能下降。这证明了结合模型先验的有效性。

技术局限与未来方向

当前局限性的深入分析

  1. 信号模型简化：使用的阻尼高斯波不能完全模拟真实神经活动的复杂性

  2. 头模型误差：依赖BEM计算的导联场矩阵，未考虑个体解剖差异

  3. 动态适应性：网络参数在训练后固定，无法适应脑状态的时间变化

有前景的扩展方向

  1. 非线性扩展：引入非凸正则化项（如Lp范数，0<p<1）进一步提升分辨率

  2. 动态网络：开发参数可随时间调整的动态网络结构

  3. 多模态融合：结合fMRI等数据改进先验约束

  4. 在线学习：实现基于实时数据的参数自适应调整

结论与影响展望

ADMM-ESINet代表了ESI领域的重要技术进步，通过巧妙结合优化理论与深度学习，解决了该领域的核心挑战。方法在保持物理可解释性的同时，实现了计算效率的显著提升。

未来，这一技术框架可扩展到其他生物电磁逆问题（如MEG源成像），并为实时脑机接口、神经反馈治疗等应用提供技术支持。开源代码的发布将促进领域的进一步发展和应用。

该方法的核心思想——通过算法展开融合模型驱动与数据驱动方法——也为其他逆问题的解决提供了有益借鉴。

http://www.dtcms.com/a/581702.html

相关文章：

  • CSS 高中低部分面试题方法及知识点介绍
  • GMI Cloud@AI周报 | Cursor 2.0发布自研模型Composer；小鹏发布新一代人形机器人 IRON
  • 莱芜手机网站建设报价网站建设平台策划
  • 【jmeter】-安装-插件安装
  • 猫头虎AI分享：CodeBuddy IDE 已支持 GLM-4.6！亲测更强了
  • 云手机能够流畅运行大型游戏吗
  • 【App开发】手机投屏的几种方式（含QtScrcpy）- Android 开发新人指南
  • 云手机 一梦江湖畅玩搬砖
  • 智享账单管理利器：Rachoon
  • 惠州网站小程序建设点网站制作的评价标准
  • Ascend C流与任务管理实战：构建高效的异步计算管道
  • 阶段性总结
  • AXI UART Lite v2.0 IP使用——ZYNQ学习笔记19
  • 延吉做网站建设通查询设通网站
  • Android创建本地plugin工程
  • 状态机实现的方法
  • 网站建设系统分析app平台搭建
  • 创建网站公司 徐州wordpress如何显示摘要
  • Aspose.word实现表格每页固定表头、最后一行填满整个页面
  • MySQL快速入门——基本查询（上）
  • 用手机看网站源代码wordpress小清新主题图片
  • 网站用什么字体做正文腾冲网站建设
  • AI Agent设计模式 Day 1：ReAct模式：推理与行动的完美结合
  • EUV光刻实战：突破7nm芯片制造的关键技术与挑战
  • #HarmonyOS篇:管理组件拥有的状态
  • 网站开启速度慢网站建设项目外包合同范本
  • 苏州手机网站建设乐清市建设规划局网站
  • 从数据节点到决策基石：以太网温湿度压力传感器的系统价值重构
  • Greensea IQ-用于国防、商业和科学领域的机器人和水下技术
  • Spring 代理的选择