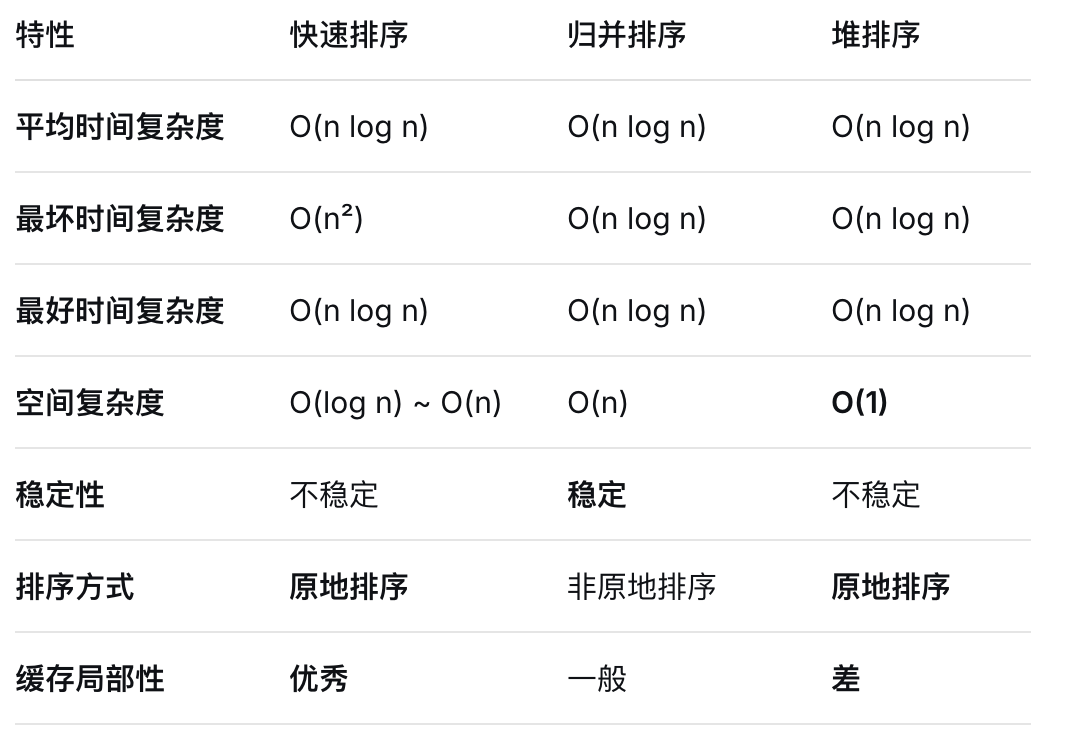
排序算法:堆排序、快速排序、归并排序
堆排序
性能:时间复杂度 O(nlogn),空间复杂度 O(1),不稳定
思路:把数组看做一个完全二叉树的结构,建立大顶堆(或小顶堆),排序就是把最顶层的根节点与末尾元素交换,然后继续从最顶层的根节点开始维护堆,循环往复就变成一个有序集合了。
大顶堆:每个节点的值都大于或等于其子节点的值。堆顶(根节点)是整个堆的最大值。
小顶堆:每个节点的值都小于或等于其子节点的值。堆顶(根节点)是整个堆的最小值。
最开始建堆时,从最后一个非叶子节点开始(因为在对一个节点进行操作时,其实是需要其子节点已经是大顶堆(或小顶堆),其实从我们要做的事情也可以理解,因为我们是要把最大或最小移动到最顶层,所以也应该是自底向上),自底向上调整堆。
代码如下:
public class HeapSort {/*** 堆排序* @param arr 待排序数组*/public static void sort(int[] arr) {int n = arr.length;// 从最后一个非叶子结点开始调整堆for (int i = n / 2 - 1; i >= 0; i--) {adjustHeapIterative(arr, i, n);}// 排序,把最大值依次放入末尾,继续调整接下来的堆for (int i = n - 1; i > 0; i--) {swap(arr, 0, i);adjustHeapIterative(arr, 0, i);}}/*** 迭代方式的堆调整(下沉)操作 O(1)* @param arr 待调整的数组* @param root 要下沉的根节点索引* @param len 堆的有效大小*/private static void adjustHeapIterative(int[] arr, int root, int len) {int temp = arr[root]; // 保存根节点的值int current = root; // 当前要调整的节点// 从根节点开始向下调整while (current * 2 + 1 < len) { // 如果有左孩子int left = current * 2 + 1;int right = current * 2 + 2;int largest = left; // 假设左孩子是较大的// 如果右孩子存在且比左孩子大if (right < len && arr[right] > arr[left]) {largest = right;}// 如果较大的孩子比当前节点大,需要交换if (arr[largest] > temp) {arr[current] = arr[largest]; // 将较大的孩子上移current = largest; // 继续向下调整} else {break; // 当前节点已经比两个孩子都大,调整结束}}arr[current] = temp; // 将最初根节点的值放到最终位置}/*** 调整堆(递归)使用递归还是会消耗栈空间* @param arr 数组* @param root 调整的根节点* @param len 边界*/private static void adjustHeap(int[] arr, int root, int len) {int tempRoot = root;int left = tempRoot * 2 + 1;int right = tempRoot * 2 + 2;// 找到最大的子节点交换if (left < len && arr[left] > arr[tempRoot]) {tempRoot = left;}if (right < len && arr[right] > arr[tempRoot]) {tempRoot = right;}// 调整有变动的子树if (tempRoot != root) {swap(arr, tempRoot, root);adjustHeap(arr, tempRoot, len);}}private static void swap(int[] arr, int a, int b) {int temp = arr[a];arr[a] = arr[b];arr[b] = temp;}}
快速排序
性能:时间复杂度 O(nlogn)~O(n^2),空间复杂度 O(log n) ~ O(n),不稳定
思路:对于一个待排序数组,选取一个基准值,把比它小的元素移动到左边,其他移动到右边,也就是左边的元素都比右边的元素小,然后再递归处理左边和右边的元素,最终有序。
基准值的选取:通常是采用随机的方式,因为理想状态是把数组对半分,这样效率是最好的,避免这个基准值过于边缘,这样可能出现最差时间复杂度 O(n^2),通过随机来进行平衡。
代码如下:
import java.util.Random;public class QuickSort {private final static Random random = new Random();public static void sort(int[] arr) {quickSort(arr, 0, arr.length - 1);}/*** 快速排序* @param arr 待排序数组* @param l 左端点* @param r 右端点*/private static void quickSort(int[] arr, int l, int r) {if (l >= r) return;// 随机选取基准值,让每次选取基准值更平均,避免出现极端情况int point = (random.nextInt() % (r - l + 1)) + l;swap(arr, l, point);// 保证左边的数都小于等于基准,右边都大于基准int i = l + 1, j = r;// 左边比基准值大的 和 右边比基准值小的 交换while (i < j) {// 两边都拿到第一个满足条件的while (i < j && arr[i] <= arr[l]) {i++;}while (i < j && arr[j] > arr[l]) {j--;}swap(arr, i, j);}if (arr[i] > arr[l]) {i--;}swap(arr, i, l);// 继续处理两边的quickSort(arr, l, i);quickSort(arr, i + 1, r);}private static void swap(int[] arr, int a, int b) {int temp = arr[a];arr[a] = arr[b];arr[b] = temp;}}
归并排序
性能:时间复杂度 O(nlogn),空间复杂度 O(n),稳定
思路:利用分治思想,把数组对半分,先把子数组排好序,最后合并结果。
代码如下:
public class MergeSort {public static void sort(int[] arr) {mergeSort(arr, 0, arr.length - 1);}private static void mergeSort(int[] arr, int l, int r) {if (l >= r) return;// 取中点,对两边进行排序int mid = l + (r - l) / 2;mergeSort(arr, l, mid);mergeSort(arr, mid + 1, r);// 合并两个有序结果merge(arr, l, mid, r);}private static void merge(int[] arr, int l, int m, int r) {int[] temp = new int[r - l + 1];int i = l, j = m + 1;int k = 0;while (i <= m && j <= r) {if (arr[i] <= arr[j]) {temp[k++] = arr[i++];} else {temp[k++] = arr[j++];}}while (i <= m) temp[k++] = arr[i++];while (j <= r) temp[k++] = arr[j++];// 用合并好的覆盖掉之前的System.arraycopy(temp, 0, arr, l, temp.length);}
}总结(deepseek)