MIT-数字棋盘和数字三角形

数字棋盘

问题描述

在一个 $n\times n$ 的数字棋盘中，每个方格都有一个数字成本 $C(i,j)$。问题是找到从第一行到最后一行的最短路径。也就是说，所有经过方格的数字成本之和最小。假设一次只能沿左对角线、右对角线或垂直方向移动一个方格。

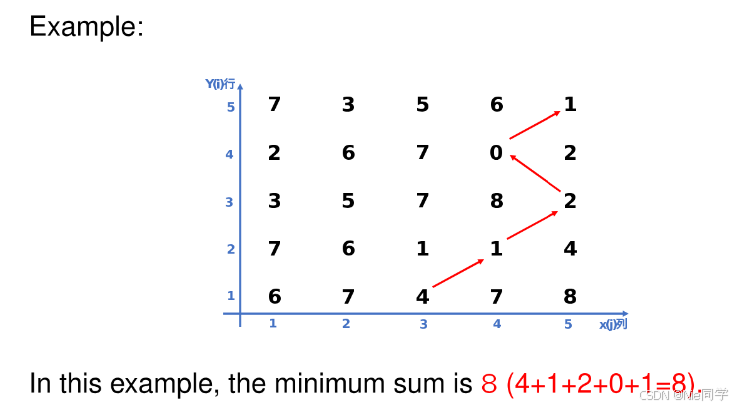
算法实现

暴力算法

首先想到的是列举出所有的路径可能，然后出这所有的路径所需的成本，找出其最小的那一个！

int c[n + 1][n + 1];int dfs(int h, int q, int j)
{q += c[h][j];if (h == n) return q;int res = INT_MAX;/* 走左对角线 */if (j - 1 >= 1)res = min(res, dfs(h + 1, q, j - 1));/* 走右对角线 */if (j + 1 <= n)res = min(res, dfs(h + 1, q, j + 1));/* 走中间 */res = min(res, dfs(h + 1, q, j));return res;
}

时间复杂度：$O(n\cdot 3^n)$

从顶行（$h=1$）出发，递归树每层最多分出 3 个分支。

假设棋盘有 $n$ 行，那么深度为 $n$（从 1 到 $n$）。

于是，递归调用数目大约是：

$$T(n)=3^{n-1}$$

• 第 1 层：1 个节点（起点）
• 第 2 层：最多 3 个节点
• 第 3 层：最多 $3^2$ 个节点
• …
• 第 $n$ 层：最多 $3^{n-1}$ 个节点

故总的结点数：

$$1+3+3^2+\dots +3^{n-1}=O(3^n)$$

我们从第一行的 每一个列 都要尝试作为起点，所以总的时间复杂度为：

$$n\times O(3^{n-1})=O(n\cdot 3^n)$$

---

动态规划（DP）

状态定义： 我们定义 $dp[i][j]$ 表示从第一行到方格 $(i,j)$ 的最短路径成本。

初始化： $dp[1][j]=c[1][j]$ 路径为 1 的路径成本就是其本身。

转移方程： $dp[i][j]=\min (dp[i-1][j-1]，dp[i-1][j],dp[i-1][j+1])+c[i][j]$

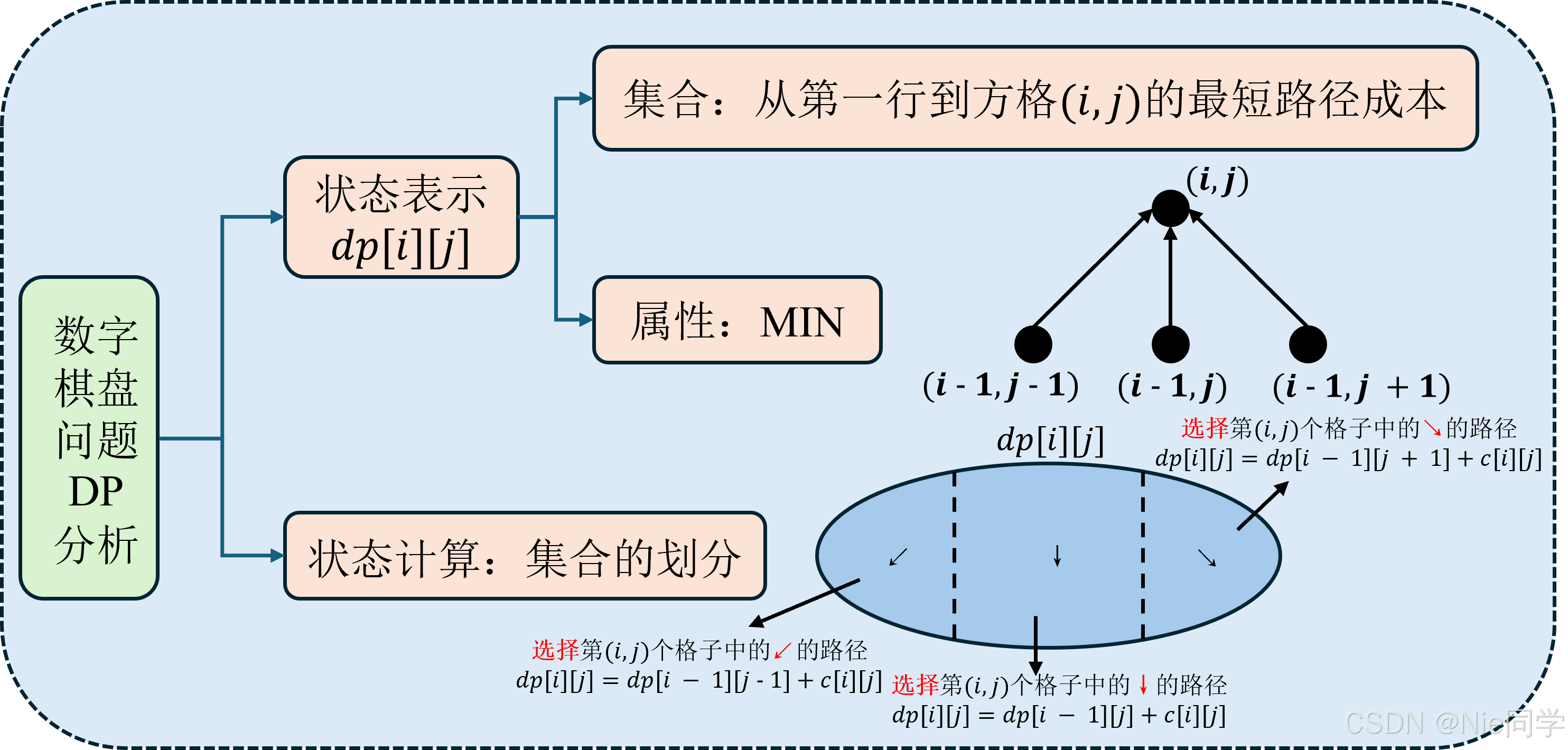
int computeQPArrays(int c[][], int n)
{int dp[n + 2][n + 2];/* 初始化dp */for (int i = 0; i <= n + 1; i ++ )for (int j = 0; j <= n + 1; j ++ ){if (i == 1) dp[i][j] = c[1][j];else dp[i][j] = INT_MAX;}for (int i = 2; i <= n; i ++ )for (int j = 1; j <= n; j ++ ){dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + c[i][j]); // 左下角dp[i][j] = min(dp[i][j], dp[i - 1][j] + c[i][j]); // 垂直dp[i][j] = min(dp[i][j], dp[i - 1][j + 1] + c[i][j]); // 右下角}int res = INT_MAX;for (int i = 1; i <= n; i ++ )res = min(res, dp[n][i]);return res;
}

时间复杂度：$O(n^2)$

---

数字三角形

问题描述

给定一个有 $n$ 行的数字三角形（每个元素都是小于 100 的正整数），问题是找到从顶顶点到最后一行顶点的路径（路径成本：$C(i,j)$），该路径的元素和最大。每次只能沿着左侧或右侧的斜线向下移动一行。

算法实现

暴力算法

暴力算法思想参考数字棋盘的暴力算法的实现方法（几乎一模一样）！

时间复杂度：$O(2^n)$

从顶行（$h=1$）出发，递归树每层分出 2 个分支。

假设棋盘有 $n$ 行，那么深度为 $n$（从 1 到 $n$）。

于是，递归调用数目大约是：

$$T(n)=2^{n-1}$$

• 第 1 层：1 个节点（起点）
• 第 2 层：2 个节点
• 第 3 层：$2^2$ 个节点
• …
• 第 $n$ 层：$2^{n-1}$ 个节点

故总的结点数：

$$1+2+2^2+\dots +2^{n-1}=O(2^n)$$

故总的时间复杂度是

$$O(2^n)$$

---

动态规划（DP）

状态定义： 我们定义 $dp[i][j]$ 表示从第一行到方格 $(i,j)$ 元素最大。

初始化： $dp[1][1]=c[1][1]$ 路径为 1 的路径成本就是其本身。

转移方程： $dp[i][j]=\min (dp[i-1][j-1]，dp[i-1][j]])+c[i][j]$

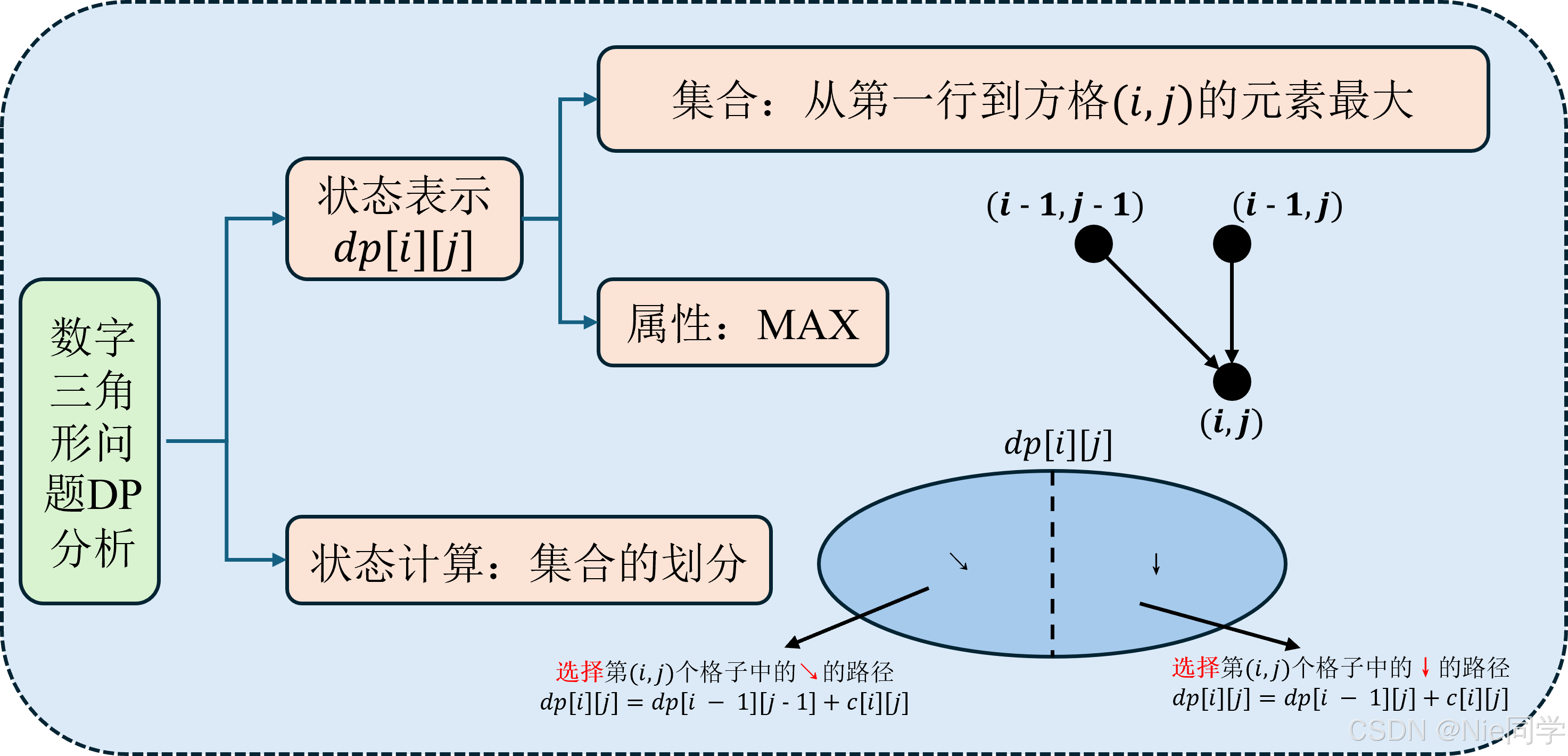
int computeQPArrays(int c[][], int n)
{int dp[n + 2][n + 2];/* 初始化dp */for (int i = 0; i <= n + 1; i ++ )for (int j = 0; j <= n + 1; j ++ )else dp[i][j] = INT_MIN;dp[1][1] = c[1][1];for (int i = 2; i <= n; i ++ )for (int j = 1; j <= i; j ++ ){dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + c[i][j]); // 右下角dp[i][j] = max(dp[i][j], dp[i - 1][j] + c[i][j]); // 垂直}int res = INT_MIN;for (int i = 1; i <= n; i ++ )res = max(res, dp[n][i]);return res;
}

时间复杂度：$O(n^2)$