数据结构—排序算法篇三
本篇博客是归并排序的讲解和一些非比较排序的讲解。
归并排序你可能没怎么听说过,但是你可能听说过有序链表的合并、有序数组的合并。归并排序就是将两个有序数组进行排序,然后在放到新的数组里形成有序。
归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序核心步骤:
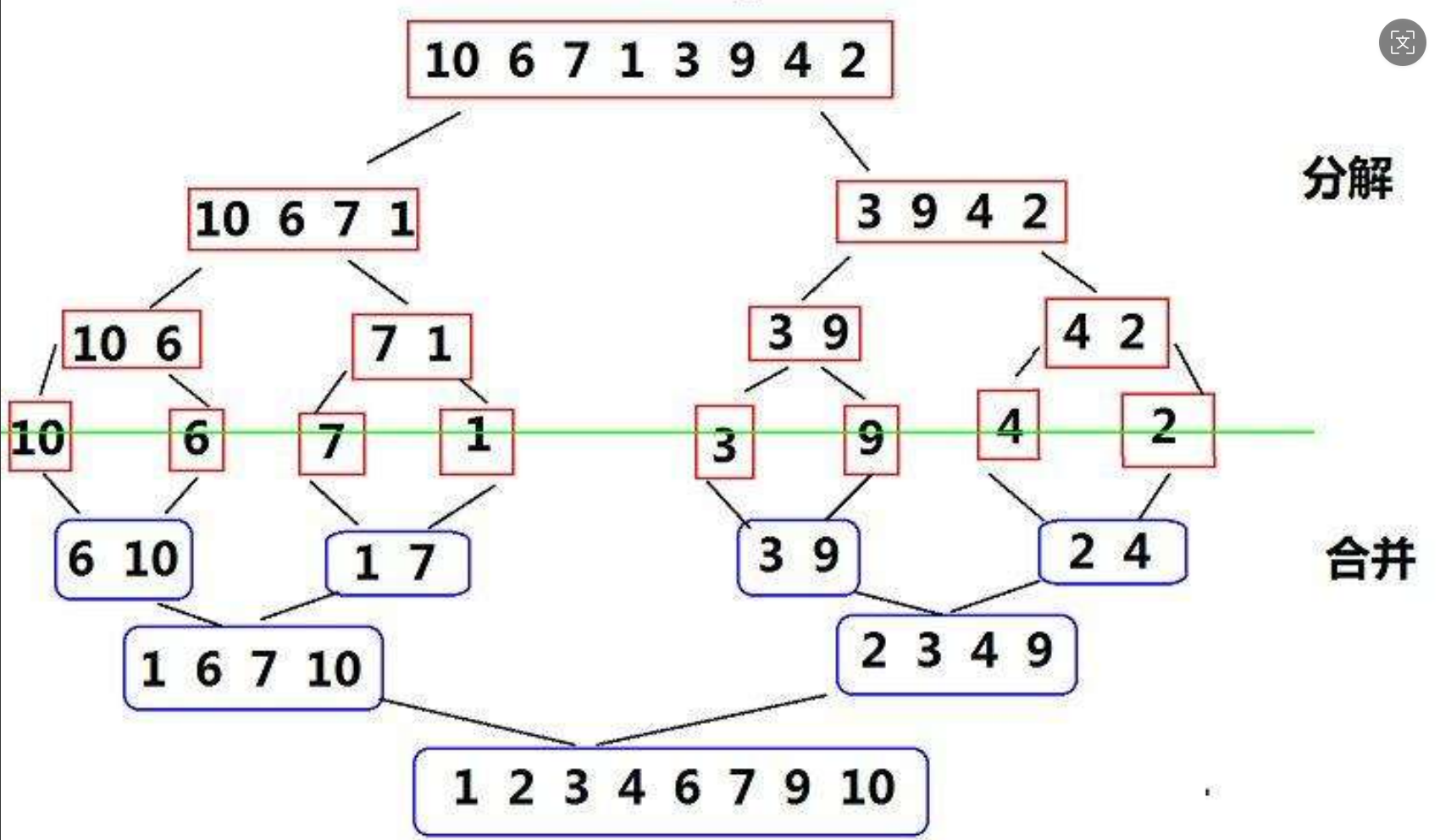
那么问题来了,如何让两个数组有序?
用递归分解法:首先把一个数组分成两半,然后去递归左右区间,区间剩下一个数进行比较。
归并排序代码
//归并排序
void _MergeSort(int* a, int* tmp, int left, int right)
{if (left == right)return;int mid = (left + right) / 2;_MergeSort(a, tmp, left, mid);_MergeSort(a, tmp, mid + 1, right);int i = left;int begin1= left, end1= mid;int begin2 = mid + 1, end2 = right;//归并while (begin1<=end1&&begin2<=end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while(begin1<=end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + left, tmp + left, (right - left + 1)*sizeof(int));}
最后一定要归并一次拷贝一次,不然如果不拷贝,原数组就变化不了,从而导致排序失败!
归并排序非递归
原理和递归差不多,只不过是用循环代替递归。
通过循环建立分组,是数据进行归并
如下图:
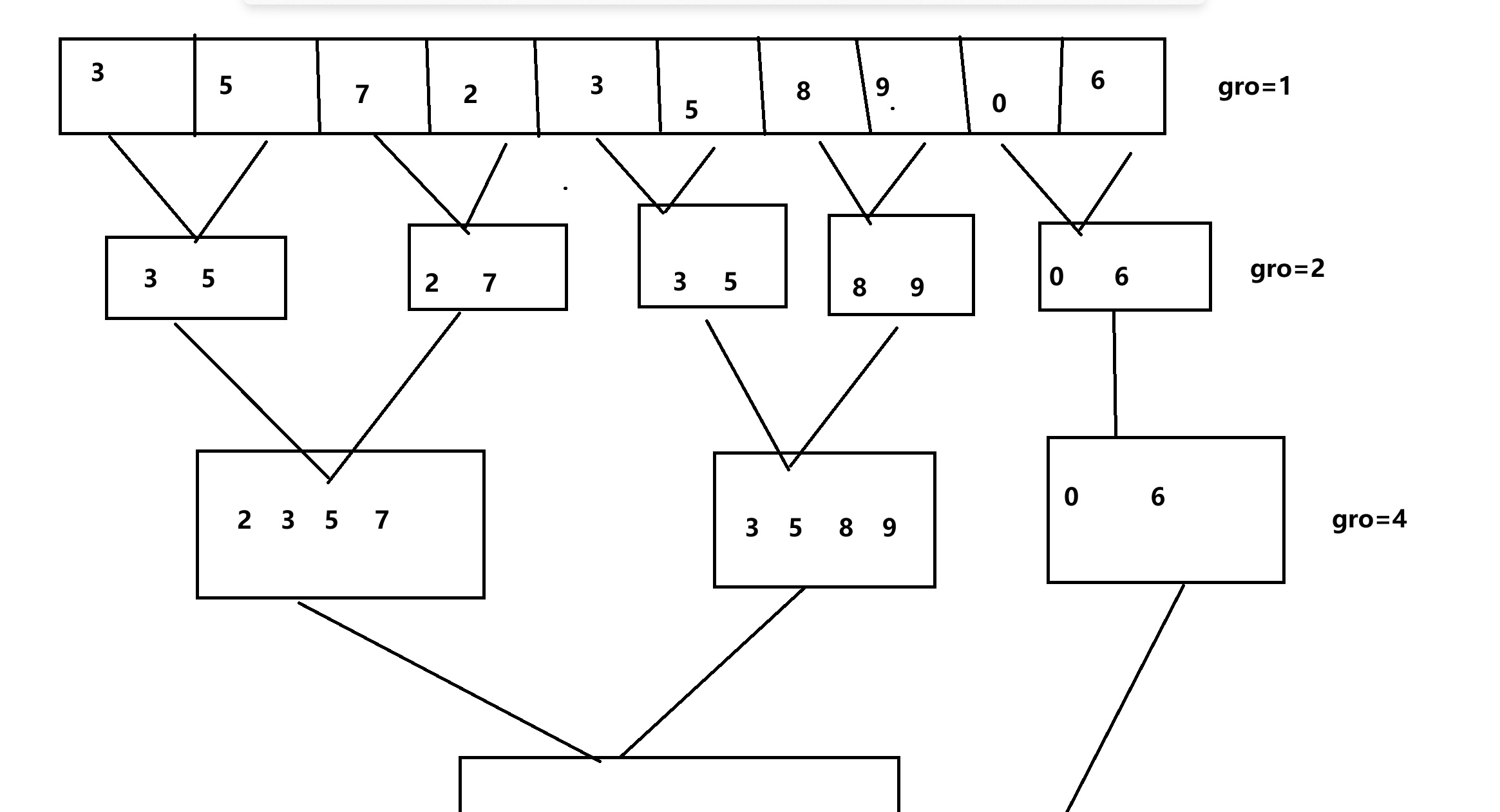
归并排序非递归代码实现
//归并排序 非递归实现
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gro = 1;while (gro < n){for (int i = 0;i < n;i += 2 * gro){int begin1 = i, end1 = i + gro - 1;int begin2 = i + gro, end2 = i + 2 * gro - 1;//归并if (begin2 >= n)break;if (end2 >= n)end2 = n - 1;int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gro = gro * 2;}free(tmp);tmp = NULL;
}最后说一下归并排序的时间复杂度是O(N*logN);空间复杂度是O(N);
非比较排序
非比较排序是一种较为特殊的排序,非比较排序是不通过元素间直接比较来排序的算法,核心优势是在特定数据场景下时间复杂度突破 O (n log n) 下限。
下面来看看三种非比较排序
- 计数排序
适用场景:数据范围 k 远小于元素个数 n,且数据为非负整数。
核心逻辑:统计每个数值出现的次数,再根据次数依次输出元素。 - 桶排序
适用场景:数据分布均匀,可划分成多个有序 “桶”。
核心逻辑:将数据分到不同桶中,对每个桶单独排序(可结合比较排序),最后合并所有桶。 - 基数排序
适用场景:数据可按位拆分(如数字、字符串),且每位的取值范围有限。
核心逻辑:按低位到高位(或反之)依次排序,每一轮用稳定排序(如计数排序)处理当前位。
计数排序
计数排序是非比较排序中最基础、最常用的算法,核心是通过 “统计元素出现次数” 来直接确定每个元素的最终位置,完全不依赖元素间的大小比较。它的优势是在数据范围可控时,能达到 O (n + k) 的线性时间复杂度(n 是元素个数,k 是数据最大值与最小值的差值),但缺点是对数据类型和范围有严格限制。通俗来讲就是统计数组元素出现的次数,再将他们统一排序
计数排序实现
void CountSort(int* a, int n)
{//选择区间int min = a[0], max = a[0];for (int i = 1;i < n;i++){if (a[i] > max){max = a[i];}if (min > a[i]){min = a[i];}}//申请空间int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (count == NULL){perror("count fail");return;}//排序for (int i = 0;i < n;i++){count[a[i] - min]++;}int j = 0;for (int i = 0;i < range;i++){while (count[i]--){a[j++] = i + min;}}
}
最后总结 计数排序不适用空间过大的数据排序,不适用浮点数排序
基数排序
基数排序(Radix Sort)是基于 “位” 排序的非比较排序,核心是按数字的每一位(或字符的每一位)依次排序,借助稳定排序(如计数排序)保证每一轮排序的有效性。它突破了比较排序的 O (n log n) 下限,时间复杂度为 O (d×(n + k))(d 是最大元素的位数,k 是每一位的取值范围),通用性比计数排序更强。
简单来说比如都是三位数的比较,先比较个位,在比较十位,在比较百位最后让他们有序,日常中有前几大排序 基本用不到基数排序。
桶排序
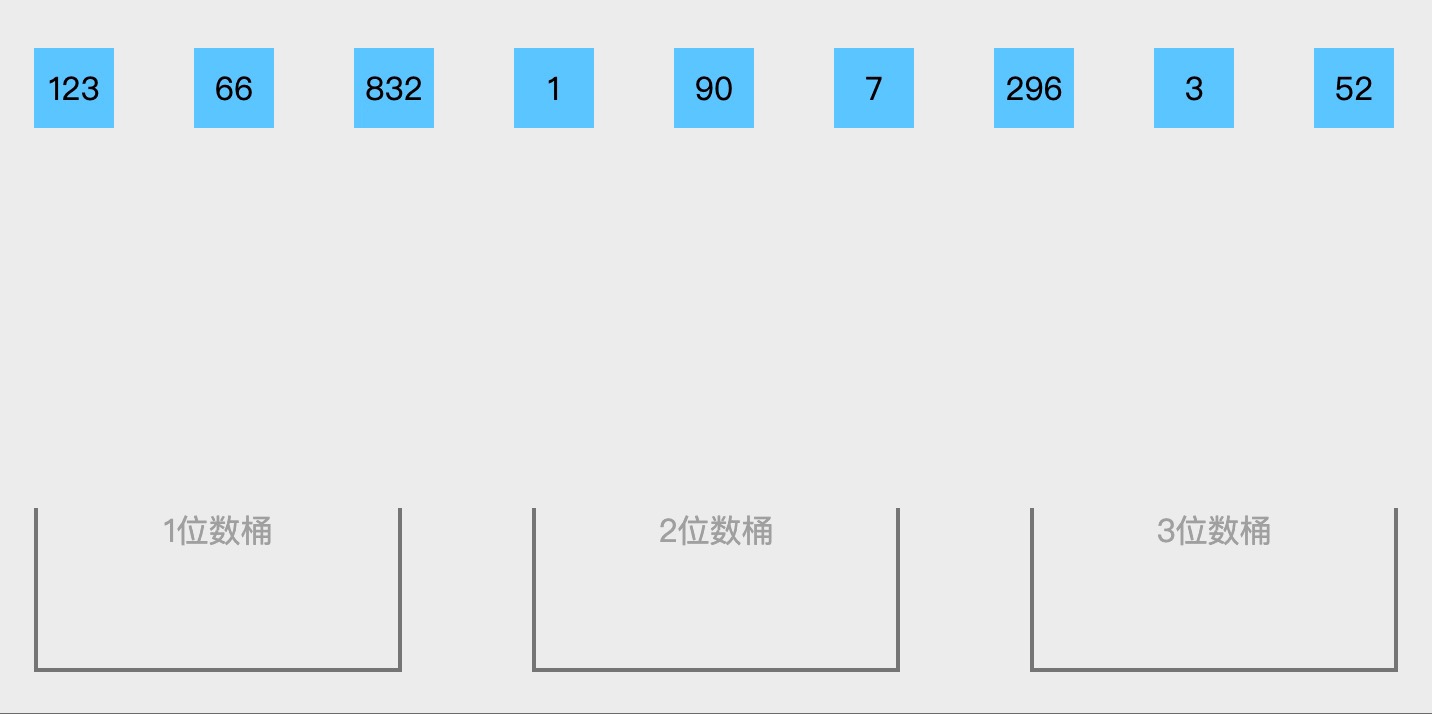
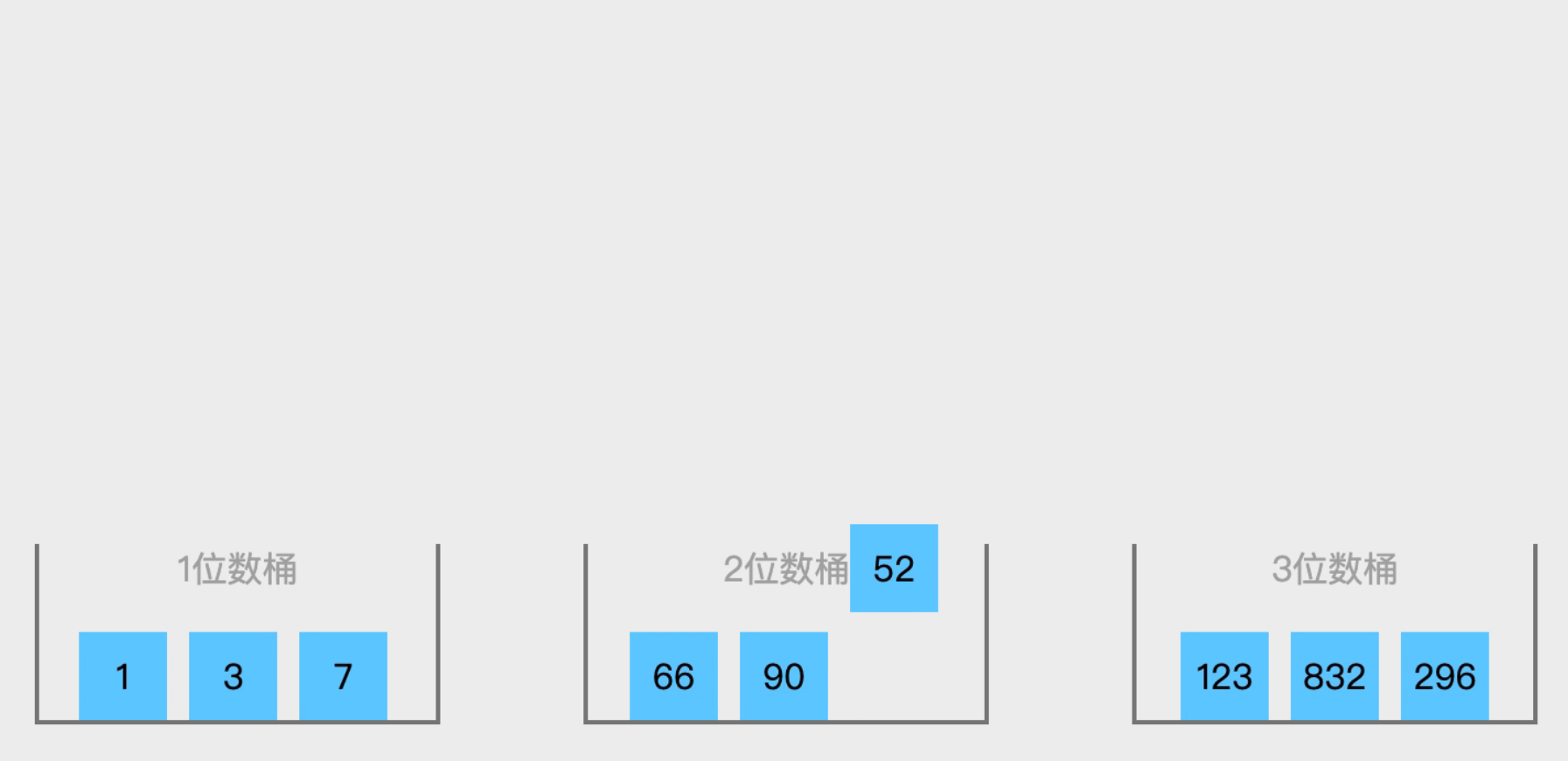
桶排序(Bucket Sort)是一种非比较排序算法,它通过将数据分到有限数量的有序 “桶” 中,分别对每个桶进行排序,最后合并结果来完成整体排序。
如下图:将他们分别放入桶中在进行排序
最后 非比较排序其实不是太重要,因为有更好的排序可以替代。所以这里简略描述一下。排序三部曲也是结束了,有些排序描述的不太好,因为太抽象了,所以尽力了。
