【分层强化学习】#1 引论：选项框架与半马尔可夫决策过程

分层强化学习

在传统强化学习框架中，对于一个任务，智能体将从一个初始状态开始，在每一个时间步进行决策，直至到达终止状态后，所获得的经验将被用于更新每一个状态下的策略。以做菜为例，这种方法在复杂、长序列任务下会面临几大难题：

• 稀疏奖励问题：在大多数复杂任务中，智能体只有在完成最终目标时才能获得奖励，过程中的每一步都是零奖励。在做菜的时候，不到最后菜品出锅，我们都很难具体评判这个菜品的好坏，更不可能为智能体抓调料、握刀等每一个细小动作都设置奖励，否则智能体可能向错误的方向学习，这使得智能体的学习效率极低。
• 信用分配问题：当一个任务需要成千上万步才能完成时，很难确定究竟是哪几步的关键决策导致了最终的成功或失败。如果菜品的口感很差，智能体很难在整个做菜的动作输出过程中精准地把握是刀工的问题还是火候的问题。
• 策略迁移与复用：许多复杂任务，或是一个复杂任务的不同过程都共享一些基本的技能。例如不同食材的处理都可能要用到“洗菜”“切菜”这些基本技能，如果把这些过程都放在不同的时间步独立学习将浪费大量经验。
• 维度灾难：随着任务状态空间和动作空间的扩大，传统强化学习的搜索空间会呈指数级增长。

正是这些问题催生了分层强化学习（Hierarchial Reinforce Learning，HRL）这一分支。顾名思义，HRL的核心思想就是“分而治之”，它将复杂任务分解为子任务由底层策略学习，如何安排子任务则由高层策略决策，进而将上述瓶颈一一攻克：

• 稀疏奖励问题：HRL为子任务设定子目标，创造更密集的内部奖励引导智能体学习。例如把“放盐”设为一个子任务，而这个任务下的策略可以只关心放盐的量是否与指令相符并以此设置奖励，至于把菜做好需要放多少盐则是高层策略考虑的问题。
• 信用分配问题：HRL将长序列决策分解为较短的子序列，使得信用分配在时间尺度上变得更加容易。将做菜过程按时间步分解会需要成千上万次决策，但如果按合理的子任务分解，高层策略可能只需十几次决策，从而更容易试出问题出现在哪几步决策上。
• 策略迁移与复用：HRL可以通过学习可复用的子策略，将学到的技能迁移到新任务中。例如“移动到某个位置”这一技能会在任何工作范围稍大的任务中使用。
• 维度灾难：HRL可以通过在不同的抽象层次上进行决策，有效地减少了每次决策需要考虑的搜索空间。例如高层策略可以分别针对上肢和下肢进行决策，使上肢只需要关注眼前的操作任务，而下肢只需要应对身体平衡。

引论将顺便介绍两个概念：选项框架和半马尔可夫决策过程，它们为HRL奠定了思想基石。

选项框架

选项框架（Options Framework）将高层策略做出的针对子任务的决策封装为选项。一个选项$o$是一个三元组$(\mathcal{I},\pi ,\beta )$，它完整地定义了一个子任务：

• 初始集$\mathcal{I}\subseteq \mathcal{S}$：规定了在哪些状态下可以启用这个选项；
• 内部策略$\pi$：一个底层策略，在执行选项时根据当前状态选择动作$a$；
• 终止条件$\beta (s)\in [0,1]$：一个函数，给出了选项在状态$s$下终止的概率。

在选项框架背景下，智能体的决策循环过程变为：

1. 当上一个选项终止时，高层策略$\mu$激活，根据当前状态$s_t$从所有在$s_t$下可用的选项集合O(st)={o∣st∈Io}\mathcal O(s_t)=\{o|s_t\in\mathcal I_o\}O(st​)={o∣st​∈Io​}中选择一个选项$o$；
2. 选项$o$的内部策略${\pi }_o$在每一个时间步根据当前状态选择动作$a$与环境交互，每次交互前检查终止条件${\beta }_o(s)$；
3. 当${\beta }_o(s)$被触发，选项$o$结束，控制权交还给高层策略$\mu$进行下一轮决策。

在选项框架下，HRL也面临一些新的挑战，包括让智能体自主学习如何创建选项、高层策略和底层策略的同步学习和终止条件的设计等等，这些都是HRL算法设计时考虑的核心问题。

半马尔可夫决策过程

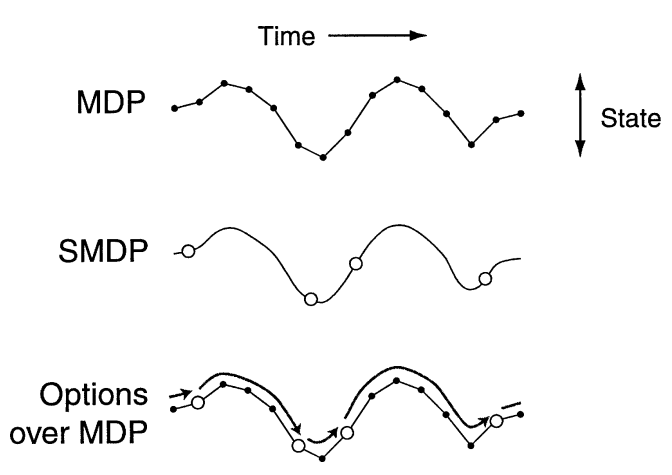
半马尔可夫决策过程（Semi-Markov Decision Process，SMDP）是马尔可夫决策过程（MDP）的扩展模型。在MDP的基础上，SMDP允许动作持续多个时间步，这恰好符合HRL中高层策略决策的特点，即决策内容为持续时间不固定的子任务。

在HRL中，SMDP的核心要素包括：

• 状态集合$\mathcal{S}$：智能体接收的环境信息，与MDP相同；
• 选项集合$\mathcal{O}$：每个选项$o\in \mathcal{O}$都是一个可以持续随机时长$\tau$的动作，替代了MDP的动作集合$\mathcal{A}$；
• 状态转移概率$P(s^{\prime },\tau |s,o)$：表示在状态$s$执行选项$o$，在$\tau$个时间步后终止于状态$s^{\prime }$的概率；
• 奖励$R(s,o)$：一个选项的奖励是在其整个执行期间所获得的所有即时奖励的总和

$$R(s,o)=\sum _{t=0}^{\tau }{\gamma }^{t}r(s_t,a_t)$$

在SMDP背景下，价值函数和贝尔曼方程的定义也随之有所调整，关键在于计算回报时采用了与选项相关的$R(s,o)$，并且折扣次数由选项的持续时间而非进行选项决策的步数决定。

状态价值函数及其贝尔曼方程

$$\begin{array}{rl}{V}^{\pi }(s)& ={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{{\tau }_t}{R}_t(s_t,o_t)\right]\\ & ={\mathbb{E}}_{\pi }[R(s,o)+{\gamma }^{\tau }{V}^{\pi }(s^{\prime })]\end{array}$$

其中$t$是进行选项决策的步数，${\tau }_t$是执行$t$步选项的累积持续时间。

动作价值函数及其贝尔曼方程

$$\begin{array}{rl}{Q}^{\pi }(s,o)& ={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{{\tau }_t}{R}_t(s_t,o_t)|s_0=s,o_0=o\right]\\ & ={\mathbb{E}}_{\pi }\left[R(s,o)+{\gamma }^{\tau }\underset{o^{\prime }}{\max }{Q}^{\pi }(s^{\prime },o^{\prime })\right]\end{array}$$

系列前瞻

本系列更新规划如下（暂时）：

1. MAXQ & HDQN：值函数分解与分层Q网络
2. Option Critic：端到端与策略梯度
3. FeUdal Networks：管理者-工作者架构
4. HIRO：目标重标记与离策略校正
5. HRL-LS & HAC：隐空间技能学习
6. DHRL：动态分层强化学习