当前位置：首页 > news >正文

深入浅出理解克尔效应（Kerr Effect）及 MATLAB 仿真实现

news 2025/11/7 9:01:56

深入浅出理解克尔效应（Kerr Effect）及 MATLAB 仿真实现

一、什么是克尔效应？

克尔效应（Kerr Effect）是一种重要的三阶非线性光学现象，指当强光通过介质时，介质的折射率会随光强变化而改变的现象。其核心特征可用公式描述：

\(n = n_0 + n_2 I\)

其中：

\(n_0\) 是介质的线性折射率
\(n_2\) 是克尔系数（非线性折射率），单位为 \(m^2/W\)
I 是光强（单位：\(W/m^2\)）

根据克尔系数的正负，可分为：

自聚焦效应：\(n_2 > 0\) 时，光强越强的区域折射率越高，光束会向中心会聚
自散焦效应：\(n_2 < 0\) 时，光强越强的区域折射率越低，光束会向四周发散

克尔效应在光通信、激光技术、光开关等领域有重要应用，例如用于制作光调制器和光限幅器。

更多内容，请参考扒谱机曾经的科普文章——【硬科普】什么是克尔效应-CSDN博客

二、仿真思路与实现方案

1. 仿真目标

我们将模拟高斯光束在具有克尔效应的介质中传播时的相位变化（自相位调制，SPM），通过可视化光强分布和相位分布，直观展示克尔效应的特性。

2. 核心物理模型

高斯光束光强分布：\(I(r) = \frac{P_0}{\pi w_0^2} e^{-2r^2/w_0^2}\)
非线性相位变化：\(\Delta\phi = \frac{2\pi}{\lambda} \Delta n \cdot z = \frac{2\pi}{\lambda} n_2 I z\)
采用周期化相位显示（\(0 \sim 2\pi\)），更直观体现相位变化规律

3. 实现步骤

设置物理参数（波长、折射率、功率等）
计算高斯光束的初始光强分布
模拟光束在介质中传播，计算不同位置的相位变化
可视化光强分布和相位分布，对比不同功率下的克尔效应

三、完整 MATLAB 代码实现

% 克尔效应（Kerr Effect）仿真：自相位调制（SPM）现象展示
% 功能：模拟不同功率高斯光束通过非线性介质时的相位变化，展示克尔效应特性
clear; clc; close all;%% 1. 参数设置
% 物理参数
lambda = 1550e-9;          % 激光波长(1550nm，常用通信波长)
n0 = 1.45;                 % 介质线性折射率(如石英光纤的折射率)
n2 = 2.6e-20;              % 非线性折射率(克尔系数，单位m²/W)
P_list = [5, 10, 50, 100]; % 不同泵浦功率(W)，用于对比克尔效应强弱
w0 = 8e-6;                 % 高斯光束腰斑半径(8μm)
L_total = 200;             % 总传播距离(m)
dz = 0.5;                  % 传播步长(m)
z = 0:dz:L_total;          % 传播距离向量
Nz = length(z);            % 传播步数% 空间网格参数
x_range = 20e-6;           % 横向范围(±20μm)
Nx = 256;                  % 横向采样点数(确保计算精度)
x = linspace(-x_range, x_range, Nx);  % 横向坐标向量
x_um = x * 1e6;            % 横向坐标(转换为μm，便于显示)
z_m = z;                   % 传播距离(m)%% 2. 预计算所有功率下的光强与相位
% 创建单元格数组存储不同功率的计算结果
I_all = cell(length(P_list), 1);   % 光强矩阵存储
phi_all = cell(length(P_list), 1); % 相位矩阵存储for p = 1:length(P_list)P0 = P_list(p);  % 当前泵浦功率% 计算高斯光束光强分布% 公式：I(r) = (P0/(πw0²)) * exp(-2r²/w0²)I0 = (P0 / (pi * w0^2)) * exp(-2 * (abs(x).^2) / w0^2);% 由于我们假设光束在横向不变(仅沿传播方向变化)，因此将初始光强复制到所有传播位置I = repmat(I0(:), 1, Nz);  % 光强矩阵(Nx×Nz)I_all{p} = I;% 计算SPM(自相位调制)引起的相位变化phi_spm = zeros(Nx, Nz);  % 相位矩阵初始化for i = 1:Nz% 计算非线性折射率变化：Δn = n2 * Idelta_n = n2 * I(:, i);% 计算相位变化：Δφ = (2π/λ) * Δn * z(i)phi_spm(:, i) = (2 * pi * delta_n * z(i)) / lambda;% 相位周期化处理(0~2π)，便于可视化相位循环特性phi_spm(:, i) = mod(phi_spm(:, i), 2*pi);endphi_all{p} = phi_spm;
end%% 3. 绘图参数设置
% 相位图参数
phi_min = 0;               % 相位显示范围下限
phi_max = 2*pi;            % 相位显示范围上限(一个完整周期)
phase_cmap = hsv(256);     % 相位色图(HSV色图适合周期特性展示)% 光强图参数
I_min = 0;                 % 光强显示范围下限
I_max = 10e11;             % 光强显示范围上限(固定值，便于对比)
intensity_cmap = turbo(256);% 光强色图%% 4. 绘制仿真结果(2×4布局：每行4个子图，分别为相位和光强)
fig = figure('Position', [100, 100, 1800, 900]);
fig.Name = '克尔效应(SPM)仿真结果';for p = 1:length(P_list)P0 = P_list(p);I = I_all{p};phi = phi_all{p};% 绘制相位分布图(第一行)subplot(2, 4, p);imagesc(x_um, z_m, phi');  % 注意矩阵转置，使维度匹配colormap(phase_cmap);      % 应用相位色图caxis([phi_min, phi_max]); % 固定相位范围colorbar;                  % 显示色标title(['相位分布 (', num2str(P0), ' W)'], 'FontSize', 10);xlabel('横向坐标 (μm)', 'FontSize', 9);ylabel('传播距离 (m)', 'FontSize', 9);xlim([min(x_um), max(x_um)]);ylim([0, L_total]);set(gca, 'YTick', 0:50:L_total);  % 设置y轴刻度axis xy;  % 确保y轴从下到上递增box on;   % 绘制边框% 绘制光强分布图(第二行)subplot(2, 4, p+4);imagesc(x_um, z_m, I');   % 注意矩阵转置colormap(intensity_cmap); % 应用光强色图caxis([I_min, I_max]);    % 固定光强范围colorbar;                  % 显示色标title(['光强分布 (', num2str(P0), ' W)'], 'FontSize', 10);xlabel('横向坐标 (μm)', 'FontSize', 9);ylabel('传播距离 (m)', 'FontSize', 9);xlim([min(x_um), max(x_um)]);ylim([0, L_total]);set(gca, 'YTick', 0:50:L_total);axis xy;box on;
endsgtitle('不同功率下的克尔效应(自相位调制)仿真', 'FontSize', 14);

四、仿真结果分析

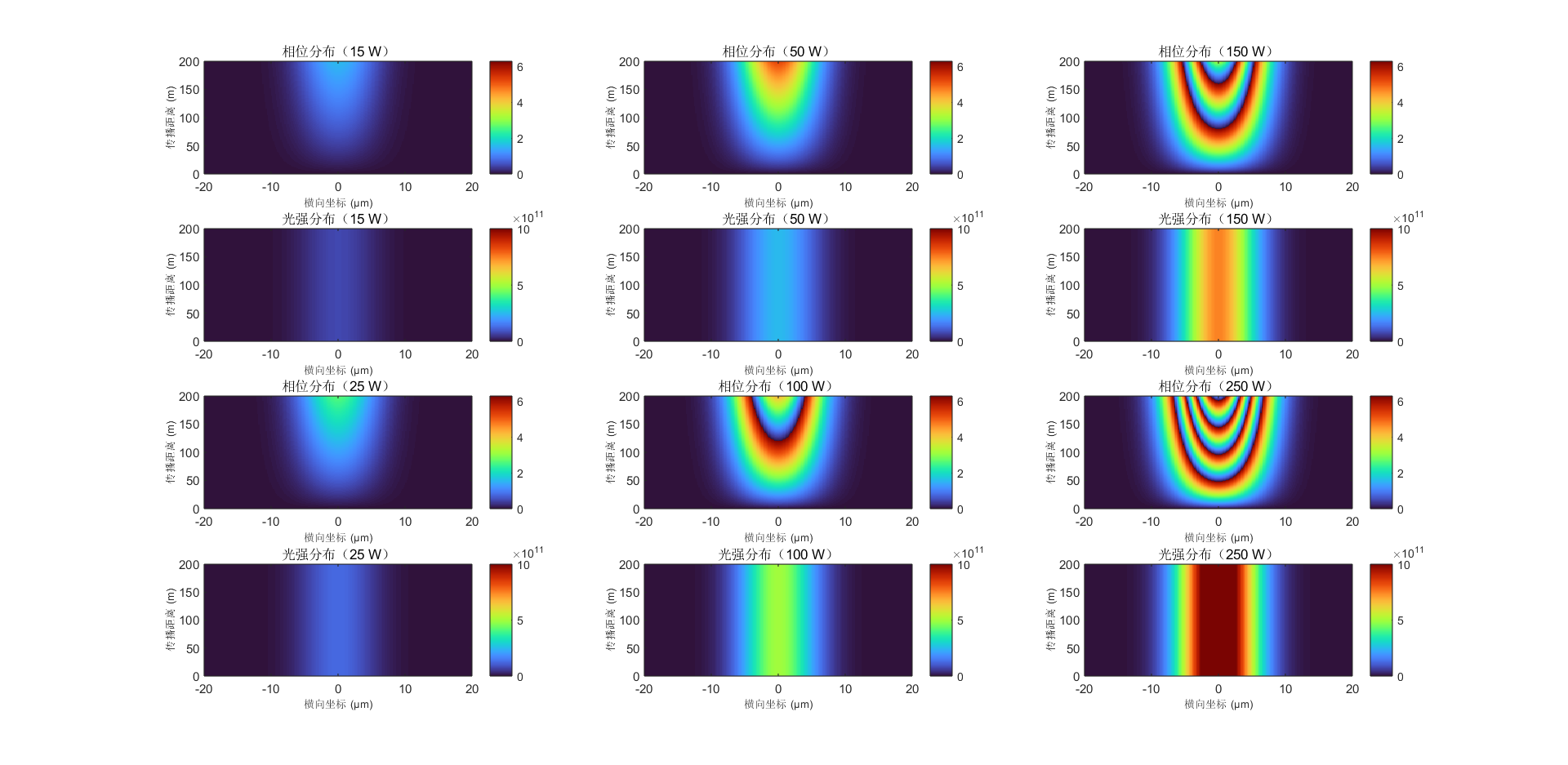
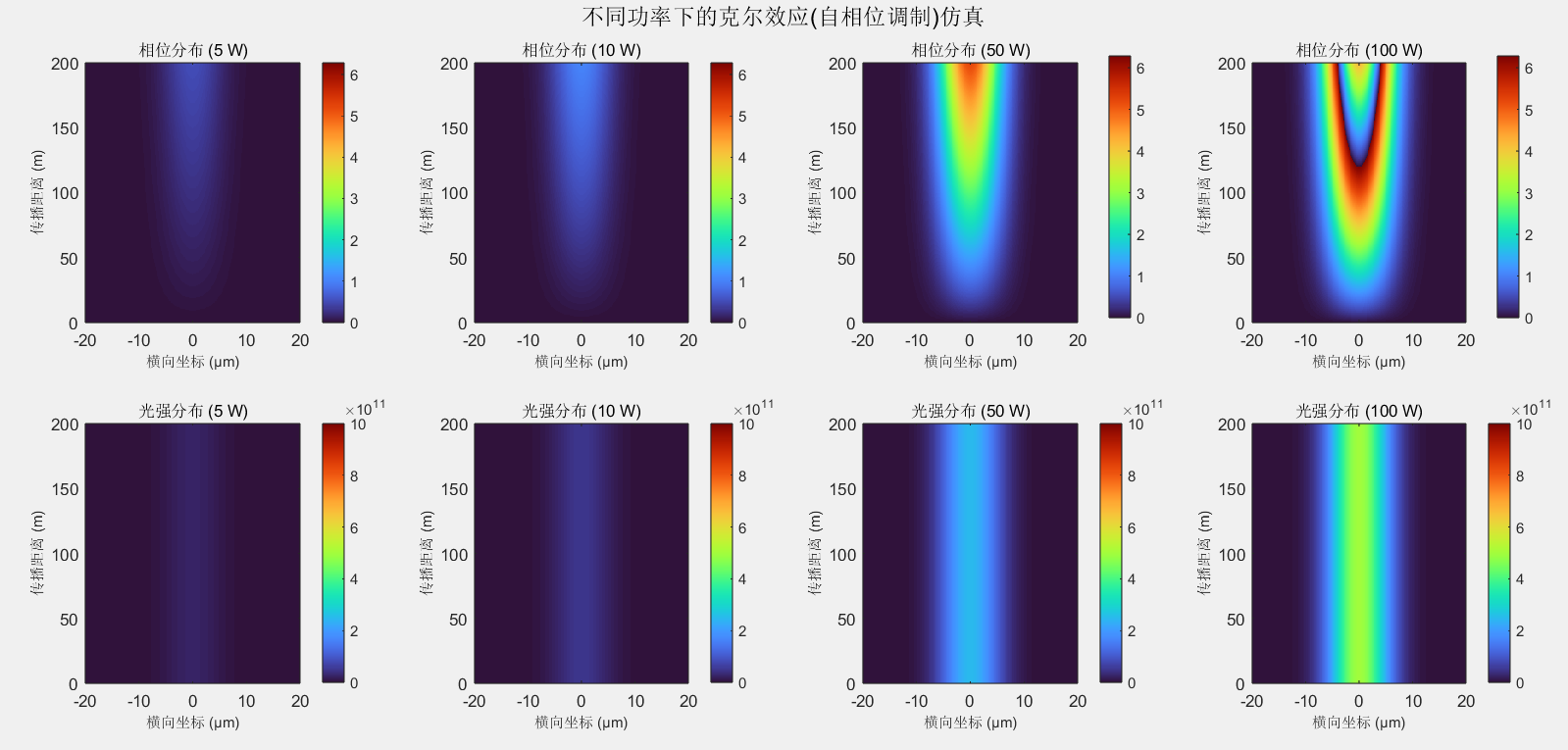
运行上述代码后，我们可以得到 4 组不同功率下的光强和相位分布对比图，从图中可以观察到：

光强分布特性：所有功率下的光强都呈现高斯分布（中心强、边缘弱），功率越高，中心光强越大。
相位变化规律：
- 相位变化与光强分布一致（中心变化快、边缘变化慢），体现了\(\Delta\phi \propto I\)的关系
- 功率越高，相位变化越剧烈（颜色循环越密集），验证了克尔效应的强度依赖性
- 相位以\(2\pi\)为周期呈现周期性变化，这是由于我们采用了mod函数进行周期化处理
克尔效应的功率依赖性：随着泵浦功率增加，自相位调制效应明显增强，这与理论预期一致。