当前位置：首页 > news >正文

复数的矩阵表示 | 欧拉恒等式的复数矩阵变换

news 2025/11/7 8:55:00

注：本文为 “复数的矩阵表示” 相关合辑。
英文引文，机翻未校。
略作重排，如有内容异常，请看原文。

Complex Numbers as Matrices: Euler’s Identity

复数作为矩阵：欧拉恒等式

Euler’s Identity below is regarded as one of the most beautiful equations in mathematics as it combines five of the most important constants in mathematics:
欧拉恒等式如下，被认为是数学中最优美的方程之一，因为它结合了数学中最重要的五个常数：

$eiπ+1=0e^{i \pi} + 1 = 0$

I’m going to explore whether we can still see this relationship hold when we represent complex numbers as matrices.
我将探索当我们用矩阵表示复数时，这种关系是否仍然成立。

Complex Numbers as Matrices
复数作为矩阵

First I’m going to define the following equivalences between the imaginary unit and the real unit and matrices:
首先，我将定义虚数单位和实数单位与矩阵之间的以下等价关系：

$i≡(0−110)1≡(1001)\begin{aligned}i &\equiv \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\\1 &\equiv \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\end{aligned}$

The equivalence for 1 as the identity matrix should make sense insofar as in real numbers, 1 is the multiplicative identity. This means that 1 multiplied by any real number gives that number. In matrices, a matrix multiplied by the identity matrix also remains unchanged. The equivalence for the imaginary unit is not as intuitive, but let’s just check that operations with complex numbers still work with this new representation.
1 作为单位矩阵的等价关系应该可以理解，因为在实数中，1 是乘法单位元，这意味着 1 乘以任何实数都等于该数。在矩阵中，一个矩阵乘以单位矩阵也保持不变。虚数单位的等价关系并不那么直观，但让我们检查一下用这种新的表示法进行复数运算是否仍然有效。

In complex numbers we have the following fundamental definition:
在复数中，我们有以下基本定义：
$i2=−1=−1(1)\begin{align*} i^2 &= -1 \\ &= -1(1) \\ \end{align*}$

Does this still work with our new matrix equivalences?
用我们的新矩阵等价关系，这是否仍然成立？

$i2≡(0−110)(0−110)=(−100−1)≡−1(1001)\begin{align*}i^2 &\equiv \begin{pmatrix}0 & -1 \\1 & 0\end{pmatrix}\begin{pmatrix}0 & -1 \\1 & 0\end{pmatrix} \\&= \begin{pmatrix}-1 & 0 \\0 & -1\end{pmatrix} \\ &\equiv -1\begin{pmatrix}1 & 0 \\0 & 1\end{pmatrix}\end{align*}$

Yes, we can see that the square of the imaginary unit gives us the negative of the multiplicative identity as required.
是的，我们可以看到，虚数单位的平方给出了所需的乘法单位元的负数。

More generally we can note that as an extension of our definitions above we have:
更一般地，作为上述定义的扩展，我们有：
$a+bi≡a(1001)+b(0−110)≡(a−bba)\begin{align*} a + bi &\equiv a \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} + b \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \\ &\equiv \begin{pmatrix} a & -b \\ b & a \end{pmatrix} \end{align*}$

Complex number multiplication

复数乘法

Let’s now test whether complex multiplication still works with matrices. I’ll choose to multiply the following 2 complex numbers:
现在我们来测试一下矩阵表示下的复数乘法是否仍然有效。我选择以下两个复数进行乘法运算：

$(1+2i)(3+4i)=(1)(3)+(1)(4)i+(2)(3)i−(2)(4)=−5+10i\begin{align*} (1 + 2i)(3 + 4i) &= (1)(3) + (1)(4)i + (2)(3)i - (2)(4) \\ &= -5 + 10i \end{align*}$

Now let’s see what happens when we do the equivalent matrix multiplication:
现在我们来看看对应的矩阵乘法结果：
$(1+2i)(3+4i)≡(1−221)(3−443)≡((1)(3)+(−2)(4)(1)(−4)+(−2)(3)(1)(4)+(2)(3)(1)(3)+(2)(−4))≡(−5−1010−5)(−5−1010−5)≡−5+10i\begin{align*} (1 + 2i)(3 + 4i) &\equiv \begin{pmatrix} 1 & -2 \\ 2 & 1 \end{pmatrix} \begin{pmatrix} 3 & -4 \\ 4 & 3 \end{pmatrix} \\ &\equiv \begin{pmatrix} (1)(3) + (-2)(4) & (1)(-4) + (-2)(3) \\ (1)(4) + (2)(3) & (1)(3) + (2)(-4) \end{pmatrix} \\ &\equiv \begin{pmatrix} -5 & -10 \\ 10 & -5 \end{pmatrix} \\ \begin{pmatrix} -5 & -10 \\ 10 & -5 \end{pmatrix} &\equiv -5 + 10i \end{align*}$

We can see we get the same result. We can obviously prove this equivalence more generally (and check that other properties still hold) but for the purposes of this post I want to check whether the equivalence to Euler’s Identity still holds with matrices.
我们可以看到结果是相同的。我们显然可以更一般地证明这种等价关系（并检查其他性质是否仍然成立），但在这篇文章中，我主要想检查欧拉恒等式与矩阵的等价关系是否仍然成立。

Euler’s Identity with matrices

矩阵形式的欧拉恒等式

If we define the imaginary unit and the real unit as the matrices above then the question is whether Euler’s Identity still holds, i.e:
如果我们将虚数单位和实数单位定义为上述矩阵，那么问题就变成了欧拉恒等式是否仍然成立，即：

$eπ(0−110)+(1001)=(0000)e^{\pi \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}} + \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

First I can note that:
首先，我们可以看到：

$πi=π(0−110)=(0−ππ0)\pi i= \pi \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -\pi \\ \pi & 0 \end{pmatrix}$

Next I can note that the Maclaurin expansion for $e^{x}$ is:
接下来，我们可以看到 $e^{x}$ 的麦克劳林展开式为：
$ex=1+∑n=1∞1n!xne^x = 1 + \sum_{n=1}^{\infty} \frac{1}{n!} x^n$

$ex=1+x+x22!+x33!+⋯e^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots$

Putting these ideas together I get:
将这些想法结合起来，我们得到：
$eiπ=1+∑n=1∞1n!(0−ππ0)ne^{i \pi} = 1 + \sum_{n=1}^{\infty} \frac{1}{n!} \begin{pmatrix} 0 & -\pi \\ \pi & 0 \end{pmatrix}^n$

This means that:
这意味着：

$eiπ=1+11!(0−ππ0)+12!(0−ππ0)2+13!(0−ππ0)3+14!(0−ππ0)4+⋯e^{i \pi} = 1 + \frac{1}{1!} \begin{pmatrix} 0 & -\pi \\ \pi & 0 \end{pmatrix} + \frac{1}{2!} \begin{pmatrix} 0 & -\pi \\ \pi & 0 \end{pmatrix}^2 + \frac{1}{3!} \begin{pmatrix} 0 & -\pi \\ \pi & 0 \end{pmatrix}^3 + \frac{1}{4!} \begin{pmatrix} 0 & -\pi \\ \pi & 0 \end{pmatrix}^4 + \cdots$

$eiπ=cos⁡π+isin⁡π=−1e^{i \pi} = \cos \pi + i \sin \pi = -1$

Next I can use the matrix multiplication to give the following:
接下来，我们可以利用矩阵乘法得到以下结果：

$eiπ=1+(0−ππ0)+12(−π200−π2)+16(0π3π30)+124(π400π4)+⋯e^{i \pi} = 1 + \begin{pmatrix} 0 & -\pi \\ \pi & 0 \end{pmatrix} + \frac{1}{2} \begin{pmatrix} -\pi^2 & 0 \\ 0 & -\pi^2 \end{pmatrix} + \frac{1}{6} \begin{pmatrix} 0 & \pi^3 \\ \pi^3 & 0 \end{pmatrix} + \frac{1}{24} \begin{pmatrix} \pi^4 & 0 \\ 0 & \pi^4 \end{pmatrix} + \cdots$

Next, I look for a pattern in each of the matrix entries and see that:
接下来，我在每个矩阵条目中寻找模式，发现：

$eiπ=1+(∑n=1∞(−1)n(2n)!π2n−∑n=1∞(−1)n(2n−1)!π2n−1∑n=1∞(−1)n(2n−1)!π2n−1∑n=1∞(−1)n(2n)!π2n)\begin{align*} e^{i \pi} &= 1 + \begin{pmatrix} \sum\limits_{n=1}^{\infty} \frac{(-1)^n}{(2n)!} \pi^{2n} & -\sum\limits_{n=1}^{\infty} \frac{(-1)^n}{(2n-1)!} \pi^{2n-1} \\[1em] \sum\limits_{n=1}^{\infty} \frac{(-1)^n}{(2n-1)!} \pi^{2n-1} & \sum\limits_{n=1}^{\infty} \frac{(-1)^n}{(2n)!} \pi^{2n} \end{pmatrix} \end{align*}$

Now, to begin with here I simply checked these on Wolfram Alpha – (these sums are closely related to the Maclaurin series for cosine and sine).
一开始，我简单地在 Wolfram Alpha 上验证了这些——这些和与余弦和正弦的麦克劳林级数密切相关。

Therefore we have:
因此，我们有：

$∑n=1∞(−1)n(2n−1)!π2n−1=−sin⁡(π)=0∑n=1∞(−1)n(2n)!π2n=cos⁡(π)−1=−2\begin{align*} \sum_{n=1}^{\infty} \frac{(-1)^n}{(2n-1)!} \pi^{2n-1} &= -\sin(\pi) &=& 0 \\ \sum_{n=1}^{\infty} \frac{(-1)^n}{(2n)!} \pi^{2n} &= \cos(\pi) - 1 &=& -2 \end{align*}$

$eiπ+1=(−100−1)+(1001)=(0000)e^{i \pi} + 1 = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} + \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

So, this means I can write:
因此，我可以写为：

$eπi=(1001)+(−200−2)=(−100−1)\begin{align*} e^{\pi i} &= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} + \begin{pmatrix} -2 & 0 \\ 0 & -2 \end{pmatrix} \\ &= \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \end{align*}$

And so this finally gives:
最终，我们得到：

$eπ(0−110)+(1001)=(−100−1)+(1001)=(0000)\begin{align*} e^{\pi \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}} &+ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} + \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \end{align*}$

$eiπ+1=0e^{i \pi} + 1 = 0$

Which is the result I wanted! Therefore we can see that Euler’s Identity still holds when we define complex numbers in terms of matrices. Complex numbers are an incredibly rich area to explore – and some of the most interesting aspects of complex numbers is their ability to “bridge” between different areas of mathematics.
这就是我想要的结果！因此，我们可以看到，当我们用矩阵来定义复数时，欧拉恒等式仍然成立。复数是一个极其丰富的研究领域——复数最有趣的方面之一是它们能够在数学的不同领域之间“架起桥梁”。

Lesson Explainer: Matrix Representation of Complex Numbers

课程讲解：复数的矩阵表示

In this explainer, we will learn how to represent a complex number as a linear transformation matrix and use this to determine the product of two complex numbers.
在这篇讲解中，我们将学习如何将复数表示为线性变换矩阵，并利用这种表示来确定两个复数的乘积。

When we first start learning about matrices, we often make connections to operations in the more familiar real numbers to help grasp the new concepts. We soon discover that there are lots of properties of matrices that do not have analogues in the real numbers. For example, matrix multiplication is, in general, noncommutative. That is, for two matrices $A$ and $B$ , $\neq BA$ in general. Nevertheless, there are helpful analogues with the real numbers that give us insightful intuition about matrices. One of the most persistent analogues with the real numbers is the correspondence between the identity matrix $I_n$ and the multiplicative identity in the real numbers: 1.
当我们刚开始学习矩阵时，我们常常将矩阵运算与熟悉的实数运算联系起来，以帮助理解新的概念。我们很快会发现，矩阵有许多性质在实数中是没有对应的。例如，矩阵乘法通常是不可交换的。也就是说，对于两个矩阵 $A$ 和 $B$ ，通常 $\neq BA$ 。然而，实数中有一些有用的对应关系可以让我们对矩阵有更深刻的直觉。实数与矩阵之间最持久的对应关系之一是单位矩阵 $I_n$ 与实数中的乘法单位元 1 之间的对应关系。

Many of the familiar properties of the multiplicative identity carry over directly to matrix algebra; for example, $I A = A I = A$ , $AA^{-1} = A^{-1}A = I_n$ , and $I_n^{-1} = I_n$ . In fact, there is a direct correspondence between the set of all matrices of the form $cI_n$ for a constant $\in \mathbb{R}$ and the real numbers, so much so that, mathematically, we can consider them to be equivalent or, to be precise, isomorphic. However, even when it comes to the analogue between the identity matrix and multiplicative identity in the reals, there are differences. In this explainer, we will explore the implications of one such difference in the case of 2-by-2 matrices.
乘法单位元的许多熟悉性质可以直接扩展到矩阵代数中；例如， $I A = A I = A$ ， $AA^{-1} = A^{-1}A = I_n$ ，以及 $I_n^{-1} = I_n$ 。实际上，所有形式为 $cI_n$ （其中常数 $\in \mathbb{R}$ ）的矩阵集合与实数之间存在直接的对应关系，以至于从数学上来说，我们可以认为它们是等价的，或者更准确地说，是同构的。然而，即使在单位矩阵与实数中的乘法单位元之间的类比中，也存在差异。在这篇讲解中，我们将探讨这种差异在 2×2 矩阵情况下的影响。

We begin by considering the square of the matrix $\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$ .
我们首先考虑矩阵 $\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$ 的平方。

Using matrix multiplication, we have
利用矩阵乘法，我们有

$M2=(0−110)(0−110)=(−100−1)M^2 = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}$ .

Interestingly, this is equal to the negative identity matrix. Hence, $M^2 = -I_2$ . What we have shown is that there exists a matrix whose square is negative the identity. This is clearly a place where the correspondence with the real numbers does not hold since there is no real number $a$ such that $a^2 = -1$ . However, there is a complex number $i$ which has this property. This leads us to a question of whether we can find some correspondence between complex numbers and 2-by-2 matrices. Since we can consider the matrix $M$ to correspond to $i$ , it makes sense that the imaginary numbers would correspond to constant multiples of $M$ . Furthermore, since there is a direct correspondence between the real numbers and constant multiples of the identity, the natural suggestion for the correspondence between matrices and complex numbers is the set of all matrices of the form $aI_2 + bM$ , where $\in \mathbb{R}$ .
有趣的是，这等于负单位矩阵。因此， $M^2 = -I_2$ 。我们已经证明了存在一个矩阵，其平方是单位矩阵的负数。这显然是一个与实数不对应的例子，因为不存在一个实数 $a$ 满足 $a^2 = -1$ 。然而，存在一个复数 $i$ 具有这种性质。这促使我们思考是否可以在复数和 2×2 矩阵之间找到某种对应关系。既然我们可以将矩阵 $M$ 视为对应于 $i$ ，那么虚数对应于 $M$ 的常数倍也是合理的。此外，由于实数与单位矩阵的常数倍之间存在直接对应关系，矩阵与复数之间的自然对应关系建议为所有形式为 $aI_2 + bM$ 的矩阵集合，其中 $\in \mathbb{R}$ 。

Rather than using the representation $aI_2 + bM$ , we can rewrite this as follows:
与其使用 $aI_2 + bM$ 的表示形式，我们也可以将其改写如下：

$aI2+bM=a(1001)+b(0−110)=(a−bba)aI_2 + bM = a \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} + b \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} a & -b \\ b & a \end{pmatrix}$

We will refer to this matrix as the matrix representation of the complex number $a + bi$ .
我们将这个矩阵称为复数 $a + bi$ 的矩阵表示。

Matrix Representation of Complex Numbers

复数的矩阵表示

We can represent the complex number $a + bi$ as the matrix
我们可以将复数 $a + bi$ 表示为矩阵
$(a−bba)\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ .

In our first example, we will explore this correspondence in relation to addition of complex numbers.
在第一个例子中，我们将探讨这种对应关系与复数加法之间的关系。

Example 1: Addition of Complex Numbers Represented as Matrices

例 1：作为矩阵表示的复数的加法

Suppose we take the matrix $\begin{pmatrix} 5 & -7 \\ 7 & 5 \end{pmatrix}$ to represent the complex number $z_1 = 5 + 7i$ and the matrix $\begin{pmatrix} 1 & -8 \\ 8 & 1 \end{pmatrix}$ to represent the complex number $z_2 = 1 - 8i$ .
假设我们用矩阵 $\begin{pmatrix} 5 & -7 \\ 7 & 5 \end{pmatrix}$ 表示复数 $z_1 = 5 + 7i$ ，用矩阵 $\begin{pmatrix} 1 & -8 \\ 8 & 1 \end{pmatrix}$ 表示复数 $z_2 = 1 - 8i$ 。

What is the sum $M + N$ ?
$M + N$ 的和是多少？
What does this represent in terms of the complex numbers $z_1$ and $z_2$ ?
这在复数 $z_1$ 和 $z_2$ 的背景下代表什么？

Answer

Part 1

We can use the definition of matrix addition to find that
我们可以利用矩阵加法的定义求得
$\begin{pmatrix} 5 & -7 \\ 7 & 5 \end{pmatrix} + \begin{pmatrix} 1 & -8 \\ 8 & 1 \end{pmatrix} = \begin{pmatrix} 6 & -15 \\ 15 & 6 \end{pmatrix}$ .

Part 2

Since $z_1 + z_2 = 6 - i$ , we can see that $M + N$ is the matrix representation of $z_1 + z_2$ .
由于 $z_1 + z_2 = 6 - i$ ，我们可以看到 $M + N$ 是 $z_1 + z_2$ 的矩阵表示。

Example 2: Multiplication of Complex Numbers Represented as Matrices

例 2：作为矩阵表示的复数的乘法

Suppose we take the matrix $\begin{pmatrix} 3 & -4 \\ 4 & 3 \end{pmatrix}$ to represent the complex number $3 - 4 i$ and the matrix $\begin{pmatrix} 2 & -5 \\ 5 & 2 \end{pmatrix}$ to represent the complex number $2 + 5 i$ .
假设我们用矩阵 $\begin{pmatrix} 3 & -4 \\ 4 & 3 \end{pmatrix}$ 表示复数 $3 - 4 i$ ，用矩阵 $\begin{pmatrix} 2 & -5 \\ 5 & 2 \end{pmatrix}$ 表示复数 $2 + 5 i$ 。

What is the product $MN$ ?
$MN$ 的乘积是多少？
What does it represent?
这代表什么？

Answer

Part 1

We can use the definition of matrix multiplication to find that
我们可以利用矩阵乘法的定义求得
$\begin{pmatrix} 2 & -5 \\ 5 & 2 \end{pmatrix} \begin{pmatrix} 3 & -4 \\ 4 & 3 \end{pmatrix} = \begin{pmatrix} -14 & -23 \\ 23 & -14 \end{pmatrix}$ .

Part 2

We first consider the product of the two complex numbers
我们首先考虑两个复数的乘积
$(3 - 4 i) (2 + 5 i) = 26 + 7 i$ .

We, therefore, see that $MN$ is the matrix representation of the product $(3 - 4 i) (2 + 5 i)$ .
因此，我们可以看到 $MN$ 是 $(3 - 4 i) (2 + 5 i)$ 的矩阵表示。

The previous example appears to indicate that the correspondence between complex numbers and these types of matrices includes multiplication. However, since we know in general that matrix multiplication is noncommutative, we should check that multiplication of matrices of this type is commutative.
前面的例子似乎表明复数与这种类型的矩阵之间的对应关系包括乘法。然而，由于我们知道矩阵乘法通常是不可交换的，我们应该检查这种类型的矩阵乘法是否是可交换的。

We let $M_1$ be the matrix representation of the complex number $z_1 = a + bi$ and $M_2$ the representation of $z_2 = c + di$ .
我们设 $M_1$ 是复数 $z_1 = a + bi$ 的矩阵表示， $M_2$ 是 $z_2 = c + di$ 的矩阵表示。

We can now consider the product $M_1 M_2$ of the matrix representations as follows:
现在我们可以考虑矩阵表示的乘积 $M_1 M_2$ ，如下所示：

$M1M2=(a−bba)(c−ddc)=(ac−bd−ad−bcad+bcac−bd)M_1 M_2 = \begin{pmatrix} a & -b \\ b & a \end{pmatrix} \begin{pmatrix} c & -d \\ d & c \end{pmatrix} = \begin{pmatrix} ac - bd & -ad - bc \\ ad + bc & ac - bd \end{pmatrix}$

Similarly, we consider the product $M_2 M_1$ :
同样，我们考虑乘积 $M_2 M_1$ ：

$M2M1=(c−ddc)(a−bba)=(ac−bd−ad−bcad+bcac−bd)M_2 M_1 = \begin{pmatrix} c & -d \\ d & c \end{pmatrix} \begin{pmatrix} a & -b \\ b & a \end{pmatrix} = \begin{pmatrix} ac - bd & -ad - bc \\ ad + bc & ac - bd \end{pmatrix}$

Hence, we can see that multiplication of matrices of this form is commutative. Furthermore, we can see that multiplying matrix representations of complex numbers directly corresponds to multiplying the complex numbers themselves.
因此，我们可以看到这种形式的矩阵乘法是可交换的。此外，我们还可以看到，复数的矩阵表示的乘法直接对应于复数本身的乘法。

At this point, we might wonder how other operations on complex numbers such as conjugation can be understood in terms of their matrix representation. Alternatively, we might ask the question the other way round: what does the determinant of a matrix represent in terms of complex numbers? In the next example, we will explore this question.
此时，我们可能会思考，复数的其他运算（如共轭）如何通过其矩阵表示来理解。或者，我们也可以反过来问：矩阵的行列式在复数中代表什么？在下一个例子中，我们将探讨这个问题。

Example 3: Interpreting the Complex Conjugation in terms of Matrices

例 3：用矩阵解释复数的共轭

Let $M$ be the matrix representation of the complex number $z = a + bi$ .
设 $M$ 是复数 $z = a + bi$ 的矩阵表示。

Express the matrix representation of $z^*$ in terms of $M$ .
用 $M$ 表示 $z^*$ 的矩阵表示。
What does $det⁡M\det M$ correspond to in relation to $z$ ?
$det⁡M\det M$ 与 $z$ 的关系是什么？
What does $M^{-1}$ correspond to in terms of $z$ ?
$M^{-1}$ 与 $z$ 的关系是什么？

Answer

Part 1

The matrix representation of $z = a + bi$ is given by $\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ . The complex conjugate of $z$ is given by $z^* = a - bi$ . We can represent this as a matrix: $(ab−ba)\begin{pmatrix} a & b \\ -b & a \end{pmatrix}$ .
复数 $z = a + bi$ 的矩阵表示为 $\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ 。 $z$ 的复数共轭为 $z^* = a - bi$ 。我们可以将其表示为矩阵 $(ab−ba)\begin{pmatrix} a & b \\ -b & a \end{pmatrix}$ 。

This represents the transpose of matrix $M$ . Hence, the matrix representation of $z^*$ is $M^T$ .
这表示矩阵 $M$ 的转置。因此， $z^*$ 的矩阵表示为 $M^T$ 。

Part 2

Recall that the determinant of a 2-by-2 matrix $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ is defined as $det⁡A=ad−bc\det A = ad - bc$ . Therefore, $det M = a^2 + b^2$ .
回顾一下，2×2 矩阵 $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ 的行列式定义为 $det⁡A=ad−bc\det A = ad - bc$ 。因此， $det M = a^2 + b^2$ 。

This corresponds to the sum of the squares of the real and imaginary parts of $z$ . Recall that the modulus of $z = a + bi$ is defined as $\sqrt{a^2 + b^2}$ . Hence, $det⁡M\det M$ corresponds to $z|^2$ .
这对应于 $z$ 的实部和虚部平方和。回顾一下，复数 $z = a + bi$ 的模定义为 $\sqrt{a^2 + b^2}$ 。因此， $det⁡M\det M$ 对应于 $z|^2$ 。

Part 3

We begin by calculating the inverse of $M$ . Recall that the inverse of a two-by-two matrix $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ is given by $A−1=1ad−bc(d−b−ca)A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$ .
我们首先计算 $M$ 的逆矩阵。回顾一下，2×2 矩阵 $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ 的逆矩阵为 $A−1=1ad−bc(d−b−ca)A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$ 。

Therefore,
因此，
$M−1=1a2+b2(ab−ba)M^{-1} = \frac{1}{a^2 + b^2} \begin{pmatrix} a & b \\ -b & a \end{pmatrix}$ .

This corresponds to the complex number $aa2+b2−ba2+b2i\frac{a}{a^2 + b^2} - \frac{b}{a^2 + b^2}i$ , which is $1z\frac{1}{z}$ . Hence, $M^{-1}$ corresponds to the complex number $1z\frac{1}{z}$ .
这对应于复数 $aa2+b2−ba2+b2i\frac{a}{a^2 + b^2} - \frac{b}{a^2 + b^2}i$ ，即 $1z\frac{1}{z}$ 。因此， $M^{-1}$ 对应于复数 $1z\frac{1}{z}$ 。

Example 4: Interpreting the Matrix Inverse in terms of Complex Numbers

例 4：用复数解释矩阵的逆

Let $M$ be the matrix representation of the complex number $z = a + bi$ . What is the corresponding complex number identity for the matrix identity $M−1=1det⁡MMTM^{-1} = \frac{1}{\det M} M^T$ , where $C$ is the cofactor matrix of $M$ ?
设 $M$ 是复数 $z = a + bi$ 的矩阵表示。矩阵恒等式 $M−1=1det⁡MMTM^{-1} = \frac{1}{\det M} M^T$ （其中 $C$ 是 $M$ 的余子矩阵）对应的复数恒等式是什么？

Answer

We begin by recalling some of the correspondences between complex numbers and their matrix representation:
我们首先回顾一下复数与其矩阵表示之间的一些对应关系：

The determinant of the matrix representation of a complex number corresponds to the square of its modulus.
复数的矩阵表示的行列式对应于其模的平方。
The transpose of the matrix representation of a complex number corresponds to complex conjugation.
复数的矩阵表示的转置对应于复数的共轭。
The inverse of the matrix representation of a complex number corresponds to the reciprocal of the complex number.
复数的矩阵表示的逆对应于复数的倒数。

These facts, however, are not sufficient to rewrite the expression as a complex number identity. We need to consider what the cofactor matrix corresponds to. Recall that the cofactor matrix of the two-by-two matrix $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ is given by $\begin{pmatrix} d & -c \\ -b & a \end{pmatrix}$ .
然而，这些事实还不足以将表达式重写为复数恒等式。我们需要考虑余子矩阵对应什么。回顾一下，2×2 矩阵 $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ 的余子矩阵为 $\begin{pmatrix} d & -c \\ -b & a \end{pmatrix}$ 。

Since $M$ represents $z = a + bi$ , we have that
由于 $M$ 表示 $z = a + bi$ ，我们有
$\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ .

Therefore, its cofactor matrix is given by
因此，其余子矩阵为
$\begin{pmatrix} a & -b \\ -b & a \end{pmatrix}$ .

Hence, the cofactor matrix of $M$ is the same as $M$ ; that is, $C = M$ . We can now use all these results to give the corresponding complex number expression for $M−1=1det⁡MMTM^{-1} = \frac{1}{\det M} M^T$ .
因此， $M$ 的余子矩阵与 $M$ 相同，即 $C = M$ 。现在我们可以利用所有这些结果，给出 $M−1=1det⁡MMTM^{-1} = \frac{1}{\det M} M^T$ 对应的复数表达式。

Since matrix inversion corresponds to reciprocation of the complex number, the left-hand side corresponds to $1z\frac{1}{z}$ . As for the right-hand side, the determinant corresponds to the square of the modulus of $z$ , $z|^2$ , and since the cofactor matrix is the same as $M$ , this corresponds to $z$ and its transpose corresponds to conjugation. Therefore, the corresponding complex number identity for $M−1=1det⁡MMTM^{-1} = \frac{1}{\det M} M^T$ is $1z=z∗∣z∣2\frac{1}{z} = \frac{z^*}{|z|^2}$ .
由于矩阵的逆对应于复数的倒数，左边对应于 $1z\frac{1}{z}$ 。对于右边，行列式对应于 $z$ 的模的平方 $z|^2$ ，并且由于余子矩阵与 $M$ 相同，这对应于 $z$ ，其转置对应于共轭。因此， $M−1=1det⁡MMTM^{-1} = \frac{1}{\det M} M^T$ 对应的复数恒等式为 $1z=z∗∣z∣2\frac{1}{z} = \frac{z^*}{|z|^2}$ 。

Now we know that the reciprocal of a complex number corresponds to the inverse of its matrix representation, we can see that complex division can be represented as multiplying the matrix representation of the numerator by the inverse matrix of the denominator.
现在我们知道复数的倒数对应于其矩阵表示的逆，我们可以看到复数的除法可以表示为将分子的矩阵表示乘以分母的逆矩阵。

Example 5: Division of Complex Numbers Represented as Matrices

例 5：作为矩阵表示的复数的除法

Let $M1=(7−11117)M_1 = \begin{pmatrix} 7 & -11 \\ 11 & 7 \end{pmatrix}$ be the matrix representation of the complex number $z_1$ and $M2=(4−114)M_2 = \begin{pmatrix} 4 & -1 \\ 1 & 4 \end{pmatrix}$ be the matrix representation of $z_2$ . Determine the matrix representation of $z1z2\frac{z_1}{z_2}$ .
设 $M1=(7−11117)M_1 = \begin{pmatrix} 7 & -11 \\ 11 & 7 \end{pmatrix}$ 是复数 $z_1$ 的矩阵表示， $M2=(4−114)M_2 = \begin{pmatrix} 4 & -1 \\ 1 & 4 \end{pmatrix}$ 是 $z_2$ 的矩阵表示。求 $z1z2\frac{z_1}{z_2}$ 的矩阵表示。

Answer

There are two ways we could calculate this. We can either use the matrix representations stating that the equivalent matrix expression for $z1z2\frac{z_1}{z_2}$ is $M_1 M_2^{-1}$ , or we can convert the matrices to their equivalent complex numbers and then undertake the complex division and convert our answer back into its matrix representation at the end. We will demonstrate the first of these methods and then use the second to check our answer.
我们有两种方法可以计算这个。我们可以使用矩阵表示，声明 $z1z2\frac{z_1}{z_2}$ 的等价矩阵表达式是 $M_1 M_2^{-1}$ ，或者我们可以将矩阵转换为它们对应的复数，然后进行复数除法，并将答案转换回矩阵表示。我们将演示第一种方法，然后使用第二种方法来验证答案。

We begin by calculating the inverse of matrix $M_2$ . Recall that the inverse of a two-by-two matrix $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ is given by $A−1=1ad−bc(d−b−ca)A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$ .
我们首先计算矩阵 $M_2$ 的逆矩阵。回顾一下，2×2 矩阵 $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ 的逆矩阵为 $A−1=1ad−bc(d−b−ca)A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$ 。

Therefore,
因此，
$M2−1=142+12(41−14)=117(41−14)M_2^{-1} = \frac{1}{4^2 + 1^2} \begin{pmatrix} 4 & 1 \\ -1 & 4 \end{pmatrix} = \frac{1}{17} \begin{pmatrix} 4 & 1 \\ -1 & 4 \end{pmatrix}$ .

We now multiply this by $M_1$ . Recall that, we do not need to worry about whether we are doing left or right multiplication since the matrices we are dealing with commute. Therefore,
现在我们将这个结果乘以 $M_1$ 。回顾一下，我们不需要担心是左乘还是右乘，因为我们处理的矩阵是可交换的。因此，

$M1M2−1=117(711−117)(41−14)=117(7×4+11×(−1)7×1+11×4(−11)×4+7×(−1)(−11)×1+4×7)=117(1751−5117)=(13−31)\begin{align*} M_1 M_2^{-1} &= \frac{1}{17}\begin{pmatrix} 7 & 11 \\ -11 & 7 \end{pmatrix}\begin{pmatrix} 4 & 1 \\ -1 & 4 \end{pmatrix} \\ &= \frac{1}{17}\begin{pmatrix} 7 \times 4 + 11 \times (-1) & 7 \times 1 + 11 \times 4 \\ (-11) \times 4 + 7 \times (-1) & (-11) \times 1 + 4 \times 7 \end{pmatrix} \\ &= \frac{1}{17}\begin{pmatrix} 17 & 51 \\ -51 & 17 \end{pmatrix} \\ &= \begin{pmatrix} 1 & 3 \\ -3 & 1 \end{pmatrix} \end{align*}$

We will check our answer using complex division. The complex number $z_1$ which the matrix $M1=(711−117)M_1 = \begin{pmatrix} 7 & 11 \\ -11 & 7 \end{pmatrix}$ represents is $z_1 = 7 - 11i$ ; similarly, $M2=(4−114)M_2 = \begin{pmatrix} 4 & -1 \\ 1 & 4 \end{pmatrix}$ is representing $z_2 = 4 + i$ . We can now calculate the quotient
我们将通过复数除法来验证这个答案。矩阵 $M1=(7−11117)M_1 = \begin{pmatrix} 7 & -11 \\ 11 & 7 \end{pmatrix}$ 表示的复数是 $z_1 = 7 - 11i$ ，矩阵 $M2=(4−114)M_2 = \begin{pmatrix} 4 & -1 \\ 1 & 4 \end{pmatrix}$ 表示的复数是 $z_2 = 4 + i$ 。现在我们计算商：

$z1z2=7−11i4+i\frac{z_1}{z_2} = \frac{7 - 11i}{4 + i}$

Multiplying the numerator and denominator by the complex conjugate of the denominator gives:
将分子和分母同时乘以分母的共轭复数，得到：

$z1z2=(7−11i)(4−i)(4+i)(4−i)=28−7i−44i+11i242+12=17−51i17=1−3i.\begin{align*} \frac{z_1}{z_2} &= \frac{(7 - 11i)(4 - i)}{(4 + i)(4 - i)} \\ &= \frac{28 - 7i - 44i + 11i^2}{4^2 + 1^2} \\ &= \frac{17 - 51i}{17} \\ &= 1 - 3i. \end{align*}$

This is represented by the matrix $(13−31)\begin{pmatrix} 1 & 3 \\ -3 & 1 \end{pmatrix}$ as expected.
这对应于矩阵 $(1−331)\begin{pmatrix} 1 & -3 \\ 3 & 1 \end{pmatrix}$ ，正如我们所期望的。

An alternative way to derive the correspondence between complex numbers and matrices is by considering transformations.
另一种推导复数与矩阵之间对应关系的方法是考虑变换。

There is a direct correspondence between linear maps and matrices: all linear maps can be represented as matrices and all matrices can be interpreted as representing some linear map. In a similar way, we can view multiplication of complex numbers as a linear transformation of the complex plane. To demonstrate the correspondence, we will consider the set of matrices representing rotations about the origin. Let us consider an anticlockwise rotation about the origin through an angle of $θ\theta$ .
线性映射与矩阵之间存在直接的对应关系：所有线性映射都可以表示为矩阵，所有矩阵都可以解释为表示某种线性映射。类似地，我们可以将复数的乘法视为复平面上的线性变换。为了展示这种对应关系，我们将考虑表示绕原点旋转的矩阵集合。假设我们考虑绕原点逆时针旋转 $θ\theta$ 角度。
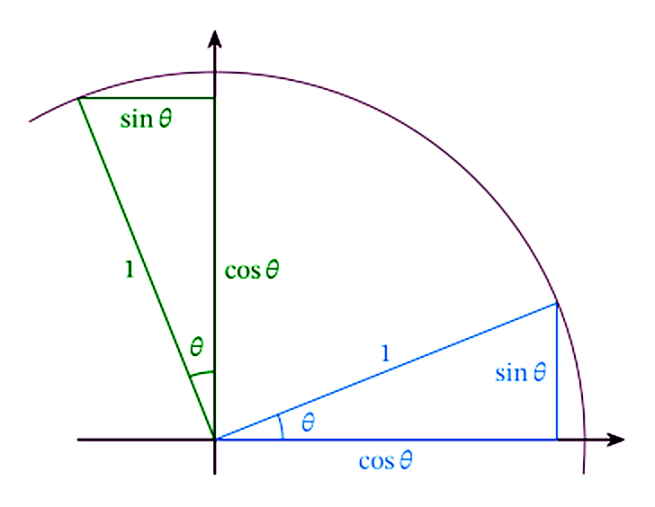
在这里插入图片描述

We consider the effect of the transformation on the two basis vectors $(1, 0)$ and $(0, 1)$ . As we can see in the diagram, $(1, 0)$ is mapped to $(cos⁡θ,sin⁡θ)(\cos \theta, \sin \theta)$ , whereas $(0, 1)$ is mapped to $(−sin⁡θ,cos⁡θ)(-\sin \theta, \cos \theta)$ . We can therefore express the matrix of this transformation as
我们考虑这个变换对两个基向量 $(1, 0)$ 和 $(0, 1)$ 的影响。正如图中所示， $(1, 0)$ 被映射到 $(cos⁡θ,sin⁡θ)(\cos \theta, \sin \theta)$ ，而 $(0, 1)$ 被映射到 $(−sin⁡θ,cos⁡θ)(-\sin \theta, \cos \theta)$ 。因此，我们可以将这个变换的矩阵表示为
$Rθ=(cos⁡θ−sin⁡θsin⁡θcos⁡θ)R_\theta = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}$

We can rewrite this as
我们可以将其重写为
$Rθ=cos⁡θ(1001)+sin⁡θ(0−110)R_\theta = \cos \theta \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} + \sin \theta \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$

This has striking similarities with Euler’s formula: $eiθ=cos⁡θ+isin⁡θe^{i \theta} = \cos \theta + i \sin \theta$ .
这与欧拉公式 $eiθ=cos⁡θ+isin⁡θe^{i \theta} = \cos \theta + i \sin \theta$ 有着惊人的相似之处。

In particular, we know that multiplication by $eiθe^{i \theta}$ represents a rotation through an angle of $θ\theta$ about the origin as does the matrix $RθR_\theta$ . Hence, we can consider $RθR_\theta$ to be the matrix representing this transformation. We can further generalize this to include multiplication by a general complex number in the form $reiθre^{i \theta}$ to find a matrix representation which we can write as
特别是，我们知道乘以 $eiθe^{i \theta}$ 表示绕原点旋转 $θ\theta$ 角度，这与矩阵 $RθR_\theta$ 是相同的。因此，我们可以认为 $RθR_\theta$ 是表示这种变换的矩阵。我们可以进一步推广这个结论，包括乘以一般形式的复数 $reiθre^{i \theta}$ ，以找到一个矩阵表示，可以写为
$(rcos⁡θ−rsin⁡θrsin⁡θrcos⁡θ)\begin{pmatrix} r \cos \theta & -r \sin \theta \\ r \sin \theta & r \cos \theta \end{pmatrix}$

which is equivalent to the matrix representation we have already considered:
这等同于我们已经考虑过的矩阵表示：
$(a−bba)\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$

We can, therefore, see that all matrices of the form $(a−bba)\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ represent transformations which consist of a rotation by some angle $θ\theta$ and a dilation by a factor of $r$ .
因此，我们可以看到所有形式为 $(a−bba)\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ 的矩阵都表示由某个角度 $θ\theta$ 的旋转和一个 $r$ 的缩放因子组成的变换。

Example 6: Translating Complex Number Expressions to Matrix Expressions

例6：将复数表达式转换为矩阵表达式

Let the complex numbers $z3z_1, z_2, \text{and } z_3$ be represented by the matrices $M3M_1, M_2, \text{and } M_3$ . Rewrite the following complex calculation as a matrix calculation:

设复数 $z_1, z_2, z_3$ 对应的矩阵为 $M_1, M_2, M_3$ 。将以下复数运算改写为矩阵运算：
$(z1∗+z2)2z3\frac{(z_1^* + z_2)^2}{z_3}$

Answer

Therefore, the complex calculation $(z1∗+z2)2z3\frac{(z_1^* + z_2)^2}{z_3}$ can be represented as a matrix calculation as follows:
复数的共轭运算对应矩阵表示的转置运算；复数的加法对应其矩阵表示的加法；由于复数的乘法对应其矩阵表示的乘法，因此复数的乘方对应矩阵的乘方；最后，复数的除法对应乘以矩阵的逆。

因此，复数运算 $(z1∗+z2)2z3\frac{(z_1^* + z_2)^2}{z_3}$ 对应的矩阵运算为：
$M_1^T + M_2)^2 M_3^{-1}$

Example 6: Translating Complex Number Expressions to Matrix Expressions

例 6：将复数表达式转换为矩阵表达式

Let the complex numbers $z_1$ , $z_2$ , and $z_3$ be represented by the matrices $M_1$ , $M_2$ , and $M_3$ . Rewrite the following complex calculation as a matrix calculation: $z_1 + z_2) z_2^* z_3$ .
设复数 $z_1$ ， $z_2$ ，和 $z_3$ 分别由矩阵 $M_1$ ， $M_2$ ，和 $M_3$ 表示。将以下复数计算重写为矩阵计算： $z_1 + z_2) z_2^* z_3$ 。

Answer

Taking complex conjugates corresponds to transposing the matrix representation. Addition of complex numbers corresponds to addition of their matrix representations. Since multiplication of complex numbers corresponds to multiplication of their matrix representations, raising to a power will correspond to raising to an equivalent power. Finally, division corresponds to multiplication by the inverse matrix. Therefore, the complex calculation $z_1 + z_2) z_2^* z_3$ can be represented as a matrix calculation as follows: $M_1 + M_2) M_2^T M_3$ .
取复数的共轭对应于矩阵表示的转置。复数的加法对应于它们的矩阵表示的加法。由于复数的乘法对应于它们的矩阵表示的乘法，因此幂运算对应于等价的幂运算。最后，除法对应于乘以逆矩阵。因此，复数计算 $z_1 + z_2) z_2^* z_3$ 可以表示为矩阵计算 $M_1 + M_2) M_2^T M_3$ 。

Key Points

要点

We can represent the complex number $a + bi$ as the matrix $(a−bba)\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ .
我们可以将复数 $a + bi$ 表示为矩阵 $(a−bba)\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ 。
Adding and multiplying complex numbers corresponds to adding or multiplying their matrix representations.
复数的加法和乘法对应于它们的矩阵表示的加法和乘法。
The determinant of the matrix representation of a complex number corresponds to the square of its modulus.
复数的矩阵表示的行列式对应于其模的平方。
The transpose of the matrix representation of a complex number corresponds to complex conjugation.
复数的矩阵表示的转置对应于复数的共轭。
The inverse of the matrix representation of a complex number corresponds to the reciprocal of the complex number.
复数的矩阵表示的逆对应于复数的倒数。
Dividing by a complex number corresponds to multiplying by the inverse of its matrix representation.
除以一个复数对应于乘以其矩阵表示的逆。

via:

Complex Numbers as Matrices: Euler’s Identity – IB Maths Resources from Intermathematics
https://ibmathsresources.com/2020/10/15/complex-numbers-as-matrices-eulers-identity/
Lesson Explainer: Matrix Representation of Complex Numbers | Nagwa
https://www.nagwa.com/en/explainers/152196980513/

查看全文

http://www.dtcms.com/a/577631.html