计算机图形学·9 几何学
本文是记录专业课“计算机图形学”的部分笔记,参考教材为Angel的第八版交互式计算机图形学——基于WebGL 2.0的自顶向下方法。
1、几何是一门研究n维空间中对象之间的关系的学科。在计算机图形学中,我们对三维空间中的对象感兴趣。我们希望一个基本几何形状的最小集合,根据这个集合可以建立起更复杂的对象——需
要三个几何要素来描述这些基本几何对象以及对象之间的关系(Scalars标量、Vectors向量、Points点)。
2、标量可以定义为集合中的成员,集合中具有两种运算(加法和乘法),运算遵从一些基本的公理(如结合律、交换律、逆)。标量自身没有几何属性、无方向,只有大小Magnitude。而向量是具有Direction方向和Magnitude长度的量。

3、Points点是空间中的位置,用大写字母表示。点与向量之间可以进行运算:点与点相减得到一个向量;等价地,点与向量相加得到一个新点,比如v=P-Q和P=Q+v等价(v是由Q指向P的向量)。我们需要注意的是,初等几何中主要应用的是笛卡尔直角坐标系,好像点和坐标关联在一起的?这种方法不是基于物理的,点的存在性应该是与坐标系的具体位置无关的、绝大多数几何结果是不依赖于坐标系的(比如欧氏几何中的全等定理)。
4、Linear/Vector Spaces 线性/向量空间是处理向量的数学系统,其中的运算有标量-向量乘法(u=αv)和向量-向量加法(w=u+v),并且在向量空间中,类似v = u + 2w − 3r的表达式有意义。注意到,向量没有位置,而对几何而言只有向量空间是不够的,还需要点。
5、Affine Spaces仿射空间可以理解为Point + vector + Scalar space,支持的运算有:①向量与向量的加法 → 向量;②标量与向量的乘法→ 向量;③点与向量的加法→ 点(直线参数化表示);④标量与标量的运算→标量。所有上述运算均与坐标无关,所以才有坐标转换。特别的,对任意点,定义1 • P = P (点)、0 • P = 0 (零向量,方向不定),零向量与任何向量都线性相关,任意一个向量组里只要有零向量,就一定是线性相关的。
6、在计算机视角中,我们采用ADT(Abstract data type,抽象数据类型),它们独立于内部表示和具体实现,数据抽象是现代计算机科学的基础。我们先来看直线的参数形式:P(α)=P0 + αd,即所有过P0点,与P0连线,且平行于向量d的点构成的直线。这种参数形式比其它形式更具一般性和稳定性,可以推广到曲线和曲面(如Explicit显式的y = mx +h 、Implicit隐式的ax + by +c =0)。此外,还有二维参数化形式,即分解到坐标(两点定义):x(α) = αx1 + (1-α)x0 和y(α) = αy1 + (1-α)y0 ,当α取[0,1]时特例为线段。
7、而在仿射中,射线与线段如下图所示。

两点线性插值就是给定点A、B,它们的仿射组合P(t)=(1-t)A+tB定义了过这两点的直线,常用于动画(如关键帧)。而到了多边形变形,给定两个有同样数目顶点的折线,利用线性插值可以给出从第一个折线到第二个折线的光滑过渡。
8、现在我们考虑“和”式:P=α1P1+α2P2+…..+αnPn,当且仅当α1+ α2+…+ αn=1时上述和式有意义,此时结果就称为点P1, P2,…, Pn 的仿射和(射线\直线的一般化)。进一步地,如果我们限定所有αi≥0,那么得到的就是P1, P2 ,…, Pn 的凸包(convex hull, 线段的一般化)。



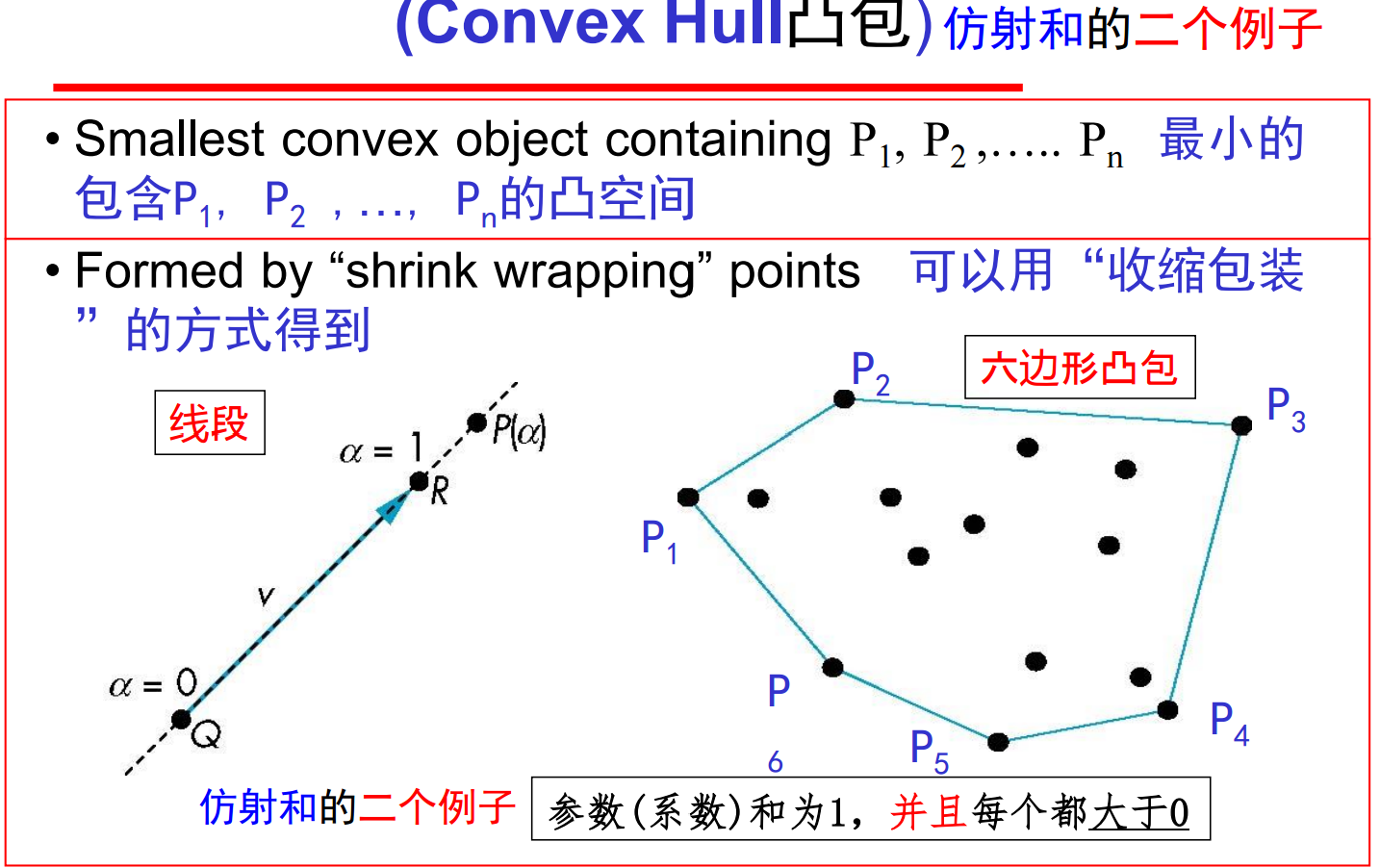
Convexity凸性:一个对象为凸的当且仅当在对象中任何两点的连接线段也在该对象内。
9、向量的点积结果是一个标量(投影的数值乘积),u·v=|u| |v| cosθ,等于0等价于二者垂直;向量的叉积结果是一个向量,长度等于|u| |v| sinθ,方向垂直于uv平面并形成右手系,等于0等价于二者平行。
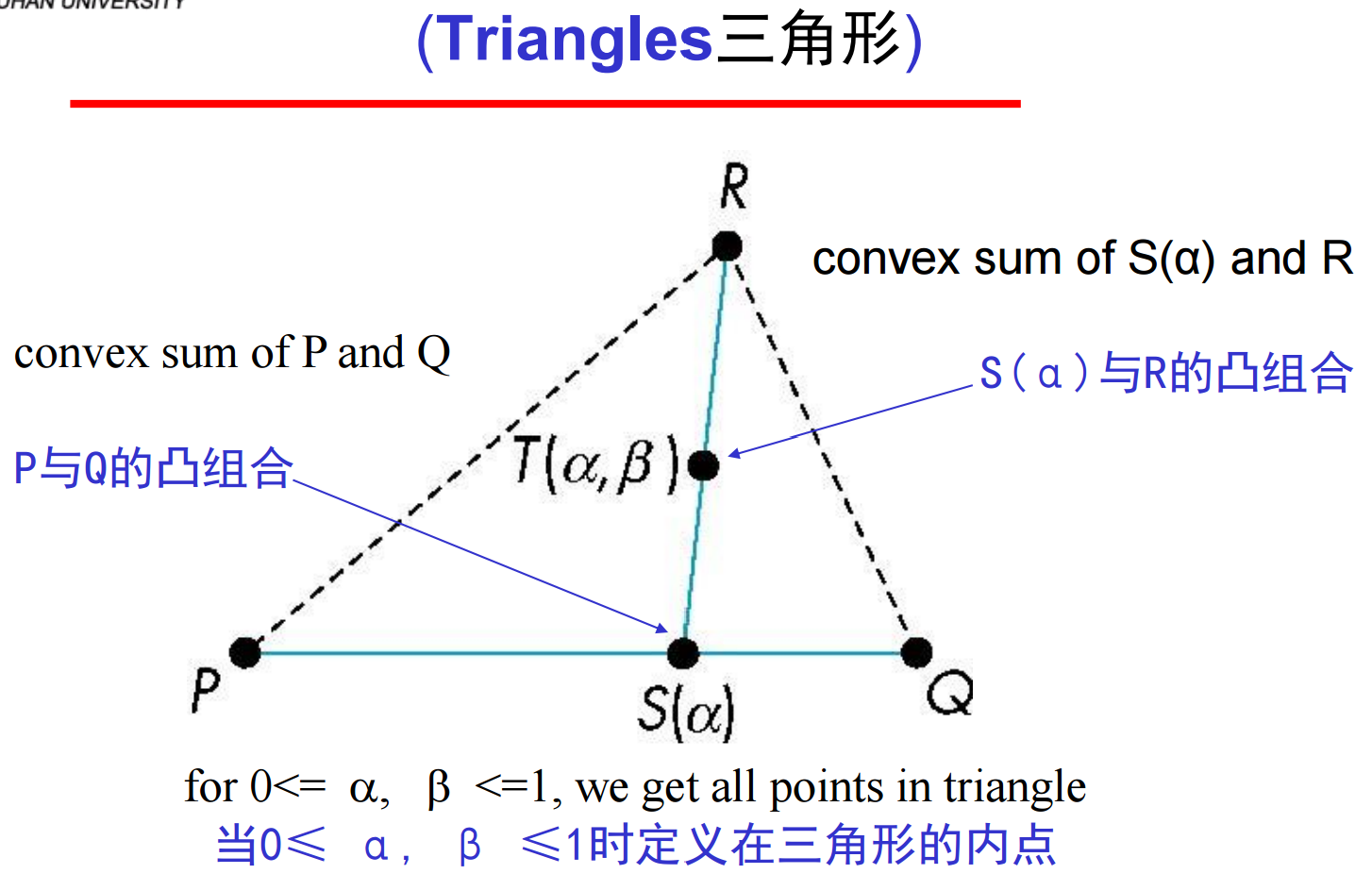
10、曲线是形式为P(α)的单参数定义的几何体,非线性;曲面是由形式为P(α, β)的两个参数定义的几何体,非线性。线性函数对应的是平面和多边形,比如双参数 + 线性 = 平面多边形。平面(Planes)平面是由一个点与两个向量或者三个点确定的(两种定义方法,即P(α,β) = R+ αu + βv和P(α,β) = R + α(Q-R) + β(P-R))。每个平面都有一个垂直于自身的向量n(法向量Normals),在平面的点与二向量形式P(α, β) = R + αu + βv中,可以应用向量的外积得到n = u × v。而对于三角形:
11、三维对象包括三维空间中曲线、三维空间中的曲面和Volumetric object实体对象。现有图形硬件软件非常适合这些三维对象,一般用对象的面来描述它,并认为是中空的;由平面凸多边形来逼近;用三维空间的一系列顶点来确定。这样,问题就转换为了如何表示点、边、多边形。
