当前位置：首页 > news >正文

【CS224N】《深度学习自然语言处理》完整版笔记

news 2025/11/7 7:42:00

写在前面：本文适合有一定机器学习 & Python基础的朋友复习使用，若零基础学习，强烈推荐李沐老师《动手学深度学习Pytorch版》！
Agent的学习不应当是速成的、浮于表面的，so~学一下CS224N，深深地理解它！
博客：https://alive0103.github.io/，欢迎来逛逛~

1. 词向量

one-hot vectors（独热向量）-是一种局部表示：
mote = [0000000000100001]
hotel = [000000010000000]

这两个向量是正交的，不存在自然意义上的相似性概念！-> 要学会从向量本身对相似性进行编码。

Note: word vectors are also called (word) embeddings or (neural) word representations They are a distributed representation
注意：词向量也被称为（单词）嵌入或（神经）单词表示形式。它们是一种分布式表示形式。

本质上我们运用距离+方向去表示语义相似度

1.1 Word2vec

有意思的问题：词向量的意思是由上下文决定的，那么当在不同的语义下，原本两个相似的词会变得不相似，那这个词向量应该怎么算？
嵌入的是其所有词义的平均值，作为该词的属性存在

corpus 语料库（拉丁语：身体）
复数：corpora 不是 corpi

方法：遍历语料库中的词（作为中心词c），设置窗口大小为m，其余词为外围词o，使得c状态下出现o的概率最高，以此往复生成句子。
计算：最大化预测准确性 -> 最小化目标函数 -> 关注平均负对数似然。
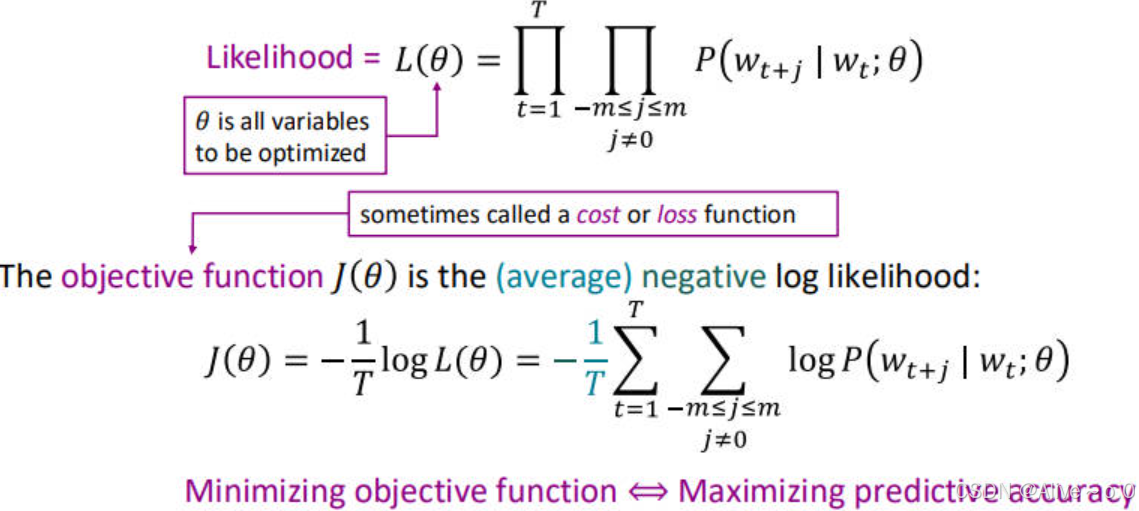
在这里插入图片描述

如何计算 $P(wt+j∣wt;θ)P(w_{t+j}\mid w_t;\theta)$ ？
$P(o∣c)=exp⁡(uoTvc)∑w∈Vexp⁡(uwTvc)P(o|c)=\frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}$

点积：点积高的两个词比较“相似”（接连出现的概率较高）
指数化：因为我们希望得到的是一个概率，点积为负数的话可以被指数成正数
分母：归一化

1.2 softmax函数

将一堆实数转换成一个概率分布。
$softmax(xi)=exp⁡(xi)∑j=1nexp⁡(xj)=pi\mathrm{softmax}(x_i)=\frac{\exp(x_i)}{\sum_{j=1}^n\exp(x_j)}=p_i$
放大了最大值的概率（max），但仍然为较小项分配了一些概率（soft）。