【训练技巧】优化器adam和adamw的公式推导详解及区别
Adam优化器公式推导详解
Adam(Adaptive Moment Estimation)结合了动量法和RMSProp的优点,通过自适应学习率实现高效优化:
-
梯度计算
在时间步ttt,计算目标函数梯度gt=∇θft(θt−1)g_t = \nabla_\theta f_t(\theta_{t-1})gt=∇θft(θt−1) -
一阶矩估计(动量)
更新梯度指数移动平均:
mt=β1mt−1+(1−β1)gtm_t = \beta_1 m_{t-1} + (1 - \beta_1) g_tmt=β1mt−1+(1−β1)gt
其中β1∈[0,1)\beta_1 \in [0,1)β1∈[0,1)控制动量衰减率(通常取0.9) -
二阶矩估计(自适应学习率)
更新梯度平方指数移动平均:
vt=β2vt−1+(1−β2)gt2v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2vt=β2vt−1+(1−β2)gt2
其中β2∈[0,1)\beta_2 \in [0,1)β2∈[0,1)(通常取0.999),gt2g_t^2gt2表示逐元素平方 -
偏差校正
因mt,vtm_t,v_tmt,vt初始为0,需进行偏差修正:
m^t=mt1−β1t\hat{m}_t = \frac{m_t}{1 - \beta_1^t}m^t=1−β1tmt
v^t=vt1−β2t\hat{v}_t = \frac{v_t}{1 - \beta_2^t}v^t=1−β2tvt -
参数更新
θt=θt−1−αm^tv^t+ϵ\theta_t = \theta_{t-1} - \alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}θt=θt−1−αv^t+ϵm^t
其中α\alphaα为学习率,ϵ≈10−8\epsilon \approx 10^{-8}ϵ≈10−8防止除零
AdamW优化器公式推导详解
AdamW(Adam with Weight Decay)改进了Adam中权重衰减的实现方式,核心区别在参数更新步骤:
-
梯度计算、矩估计、偏差校正步骤与Adam完全相同
-
参数更新(关键改进)
θt=θt−1−α(m^tv^t+ϵ+λθt−1)\theta_t = \theta_{t-1} - \alpha \left( \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} + \lambda \theta_{t-1} \right)θt=θt−1−α(v^t+ϵm^t+λθt−1)
其中λ\lambdaλ为权重衰减系数
核心区别分析
| 特性 | Adam | AdamW |
|---|---|---|
| 权重衰减 | 融入损失函数:L′=L+λ2∣θ∣2L' = L + \frac{\lambda}{2}|\theta|^2L′=L+2λ∣θ∣2 | 直接作用于参数更新 |
| 数学表达 | 梯度含衰减项:gtAdam=∇L+λθg_t^{Adam} = \nabla L + \lambda \thetagtAdam=∇L+λθ | 梯度纯净:gt=∇Lg_t = \nabla Lgt=∇L |
| 耦合性 | 衰减项与自适应学习率耦合 | 衰减项与自适应学习率解耦 |
| 物理意义 | 衰减强度受vt\sqrt{v_t}vt影响 | 衰减强度保持恒定 |
区别图示
# Adam更新(伪代码)
grad = compute_gradient() + weight_decay * param
m = beta1*m + (1-beta1)*grad
v = beta2*v + (1-beta2)*grad**2
param -= lr * m / (sqrt(v) + eps)# AdamW更新(伪代码)
grad = compute_gradient() # 无衰减项
m = beta1*m + (1-beta1)*grad
v = beta2*v + (1-beta2)*grad**2
param -= lr * (m / (sqrt(v) + eps) + weight_decay * param)
为什么AdamW更优?
-
解耦优势
在Adam中,权重衰减项λθ\lambda\thetaλθ会被自适应学习率α/vt\alpha/\sqrt{v_t}α/vt缩放,导致实际衰减强度随训练动态变化。AdamW保持λ\lambdaλ独立作用,确保正则化效果稳定。 -
实验验证
- 在ImageNet上,AdamW相比Adam可获得+0.5%+0.5\%+0.5%至+1.5%+1.5\%+1.5%精度提升
- 训练收敛速度提升约1.2×1.2\times1.2×(相同迭代次数下损失更低)
-
超参数鲁棒性
AdamW对λ\lambdaλ的选择更鲁棒,λ\lambdaλ在[10−3,10−2][10^{-3}, 10^{-2}][10−3,10−2]范围通常有效,而Adam需要精细调整。
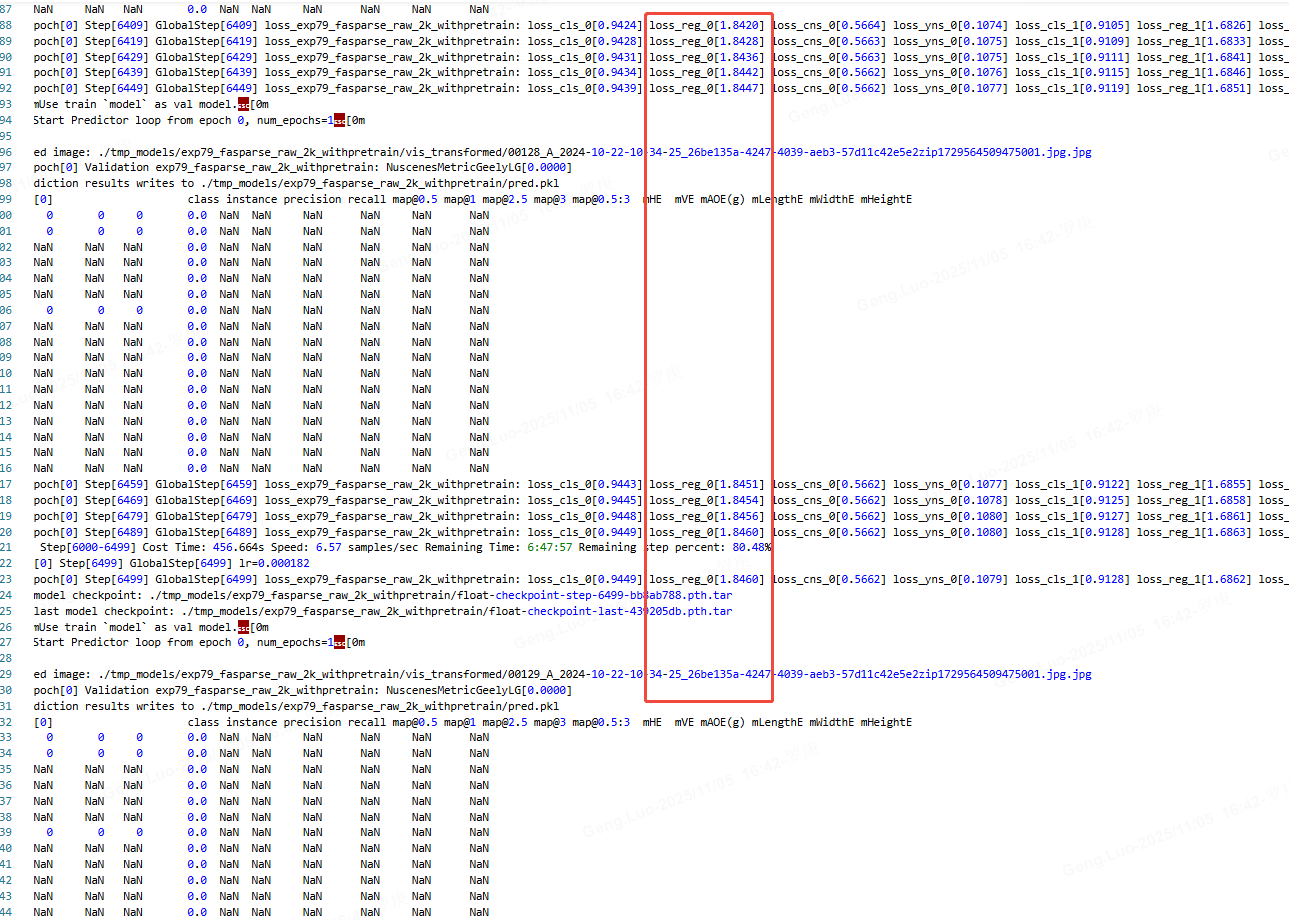
效果对比:
adam
loss从1.2慢慢增加到1.8去了,收敛困难。
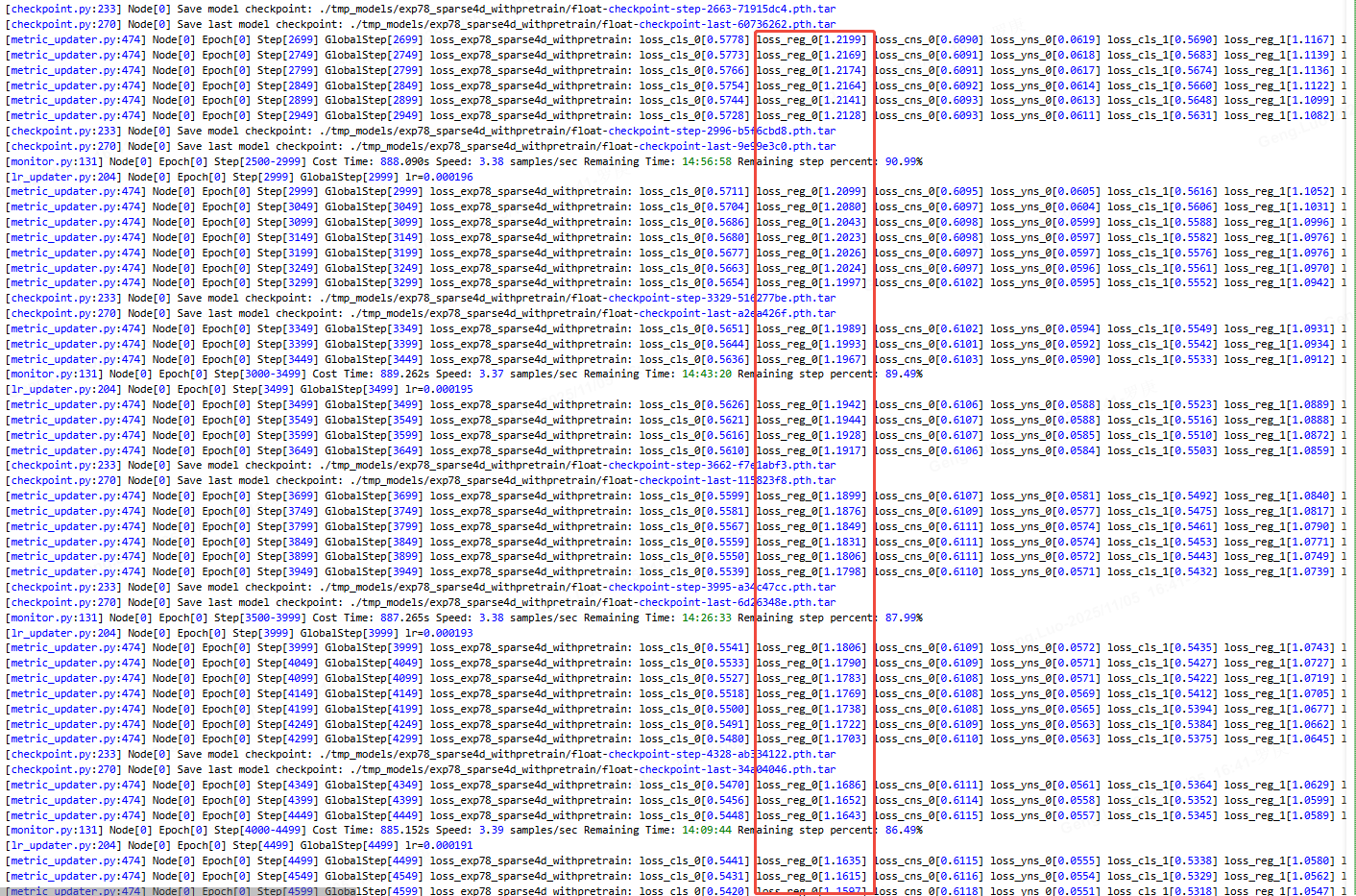
adamw
loss从1.2慢慢下降,收敛正常。
实践建议:当使用Adam类优化器时,优先选择AdamW并设置λ∈[0.01,0.1]\lambda \in [0.01, 0.1]λ∈[0.01,0.1],初始学习率α\alphaα设为Adam的1/21/21/2至1/101/101/10。
