数据结构之**二叉树**超全秘籍宝典2
文章目录
- *1. 前言*
- *2. 正文*
- 1. 二叉树的练习题
- *3. 结语*
“你的每一分耕耘，都藏着未来的收获与惊喜”
1. 前言
本文主要围绕链式二叉树的习题展开，请大家跟进小编的步伐！！ 🌹🌹🌹
2. 正文
1. 二叉树的练习题
- 检查两棵树是否为相同的树，首先判断是否为相同的树需要两点，
（1）结构相同
（2）节点具有相同的值
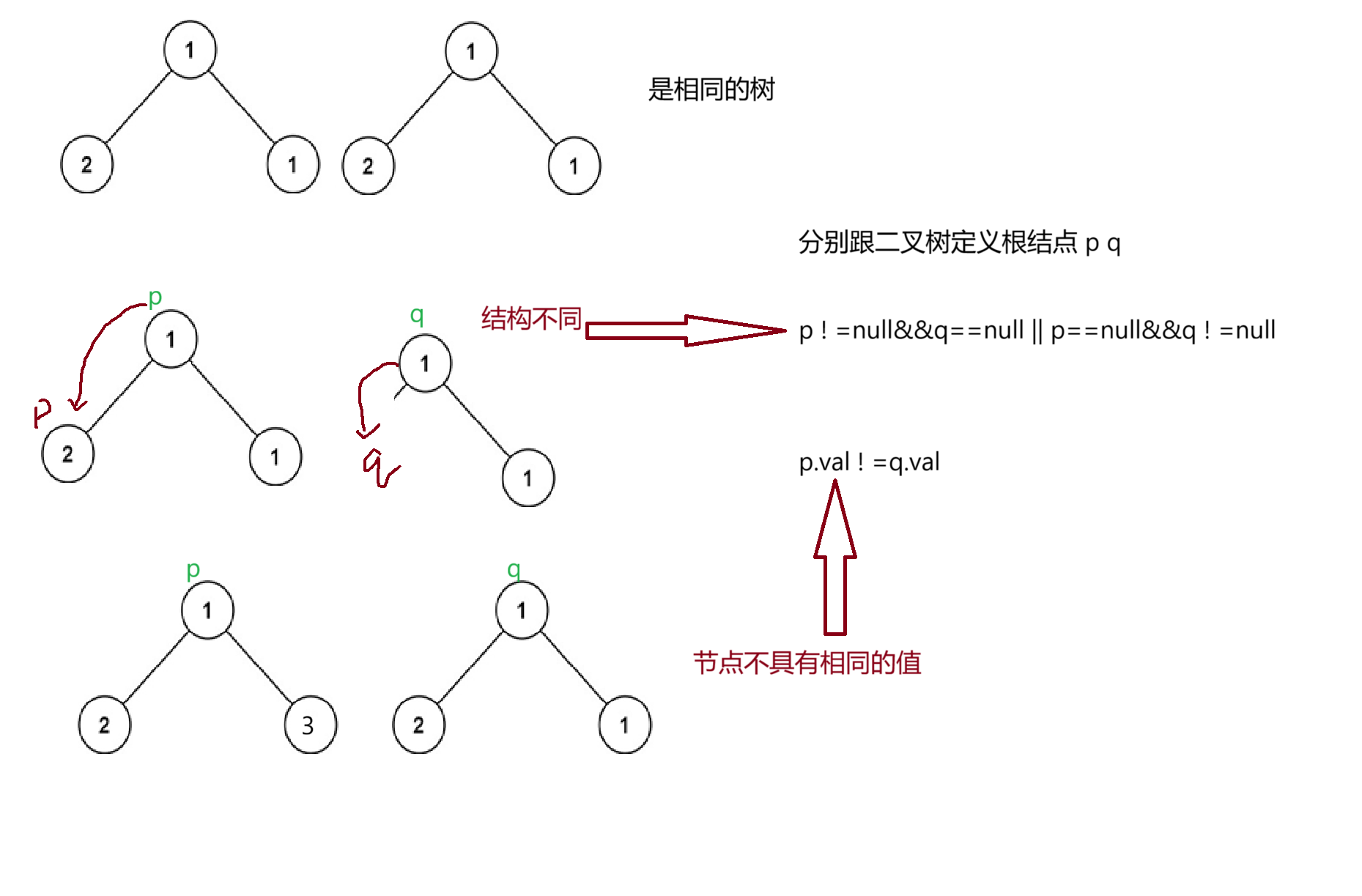根据图上的思路我们的代码很简单就完成了
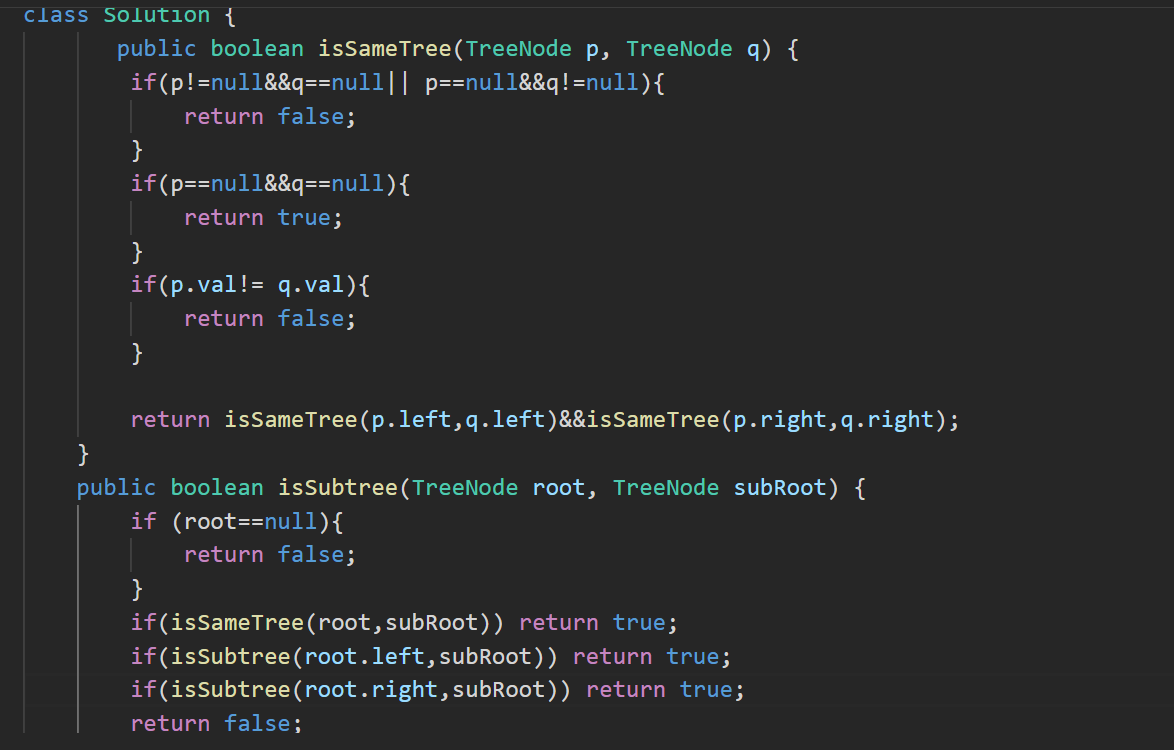
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p!=null&&q==null|| p==null&&q!=null){return false;}if(p==null&&q==null){return true;}if(p.val!= q.val){return false;}return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}
}
这里注意一点 第二个if语句与第三个if语句的顺序不能交换！！先判断当前节点是否为空再判断值
- 是否为另一棵树的子树
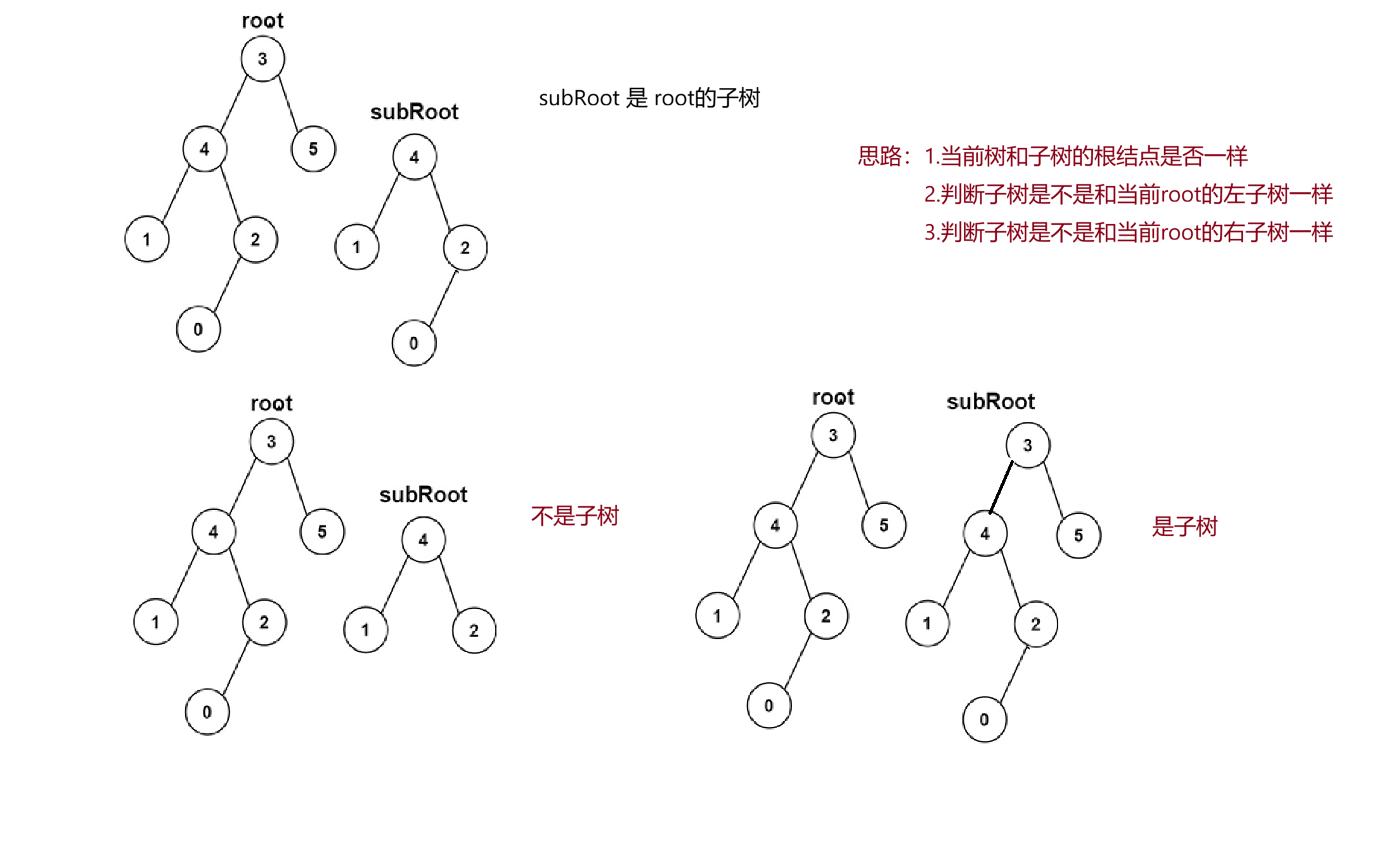
我们用代码来完善
注意这里必须要讨论root==null的情况，root是在遍历树，所以会出现root为空的情况，如果root为null还没有匹配子树，那么就return false
这里我们还需要用到第一题的方法，如果根结点与子树相同，则返回true，
不相同再判断左子树与子树是否相同，采用递归的思想
public boolean isSubtree(TreeNode root, TreeNode subRoot) {if (root==null){return false;}if(isSameTree(root,subRoot)) return true;if(isSubtree(root.left,subRoot)) return true;if(isSubtree(root.right,subRoot)) return true;return false;}
- 翻转二叉树
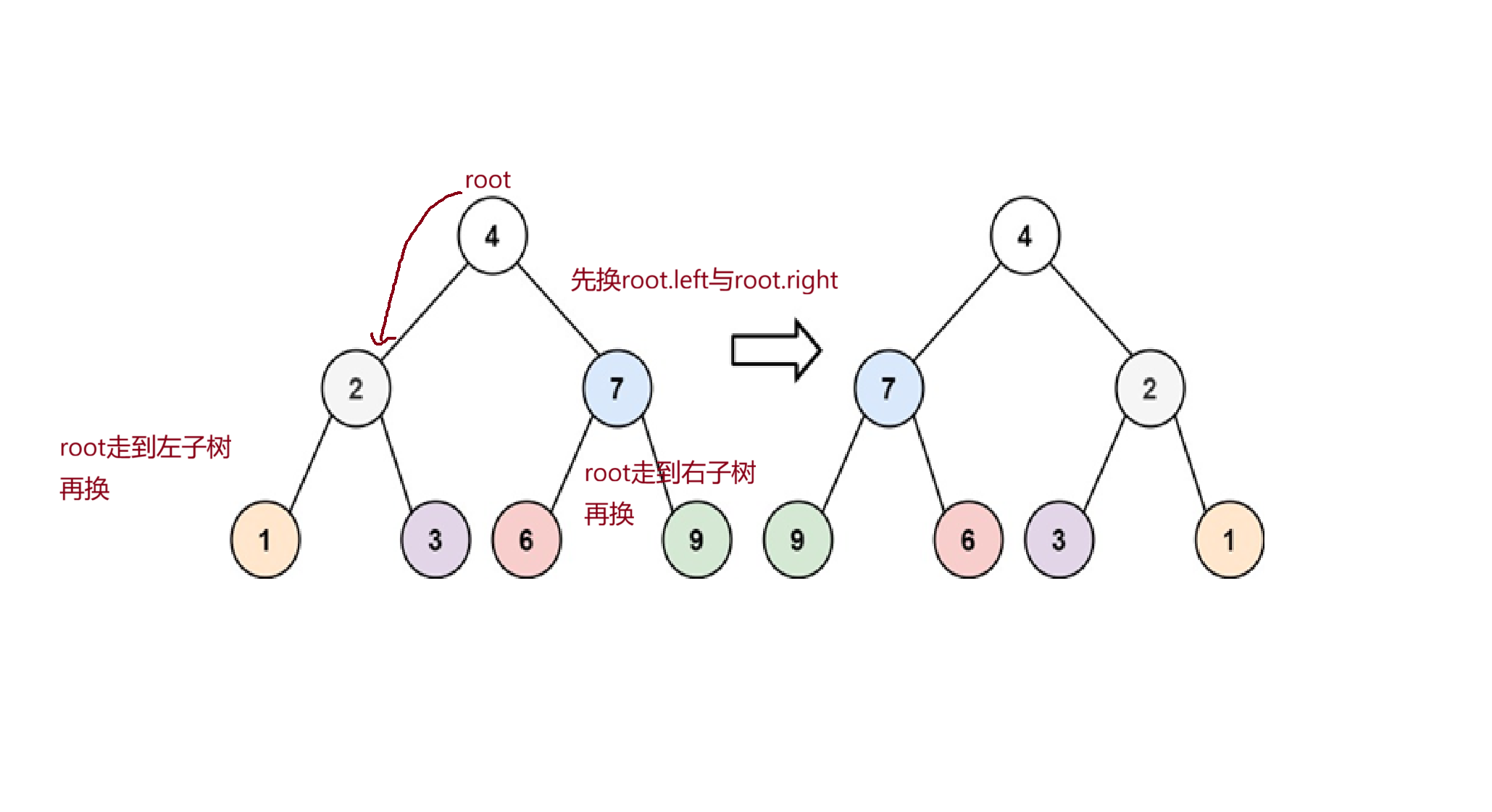对于这个操作的实现还是很简单的
public TreeNode invertTree(TreeNode root) {if(root==null){return null;}TreeNode tmp=root.left;root.left=root.right;root.right=tmp;invertTree(root.left);invertTree(root.right);return root;}
- 对称二叉树，判断一棵树是否为对称二叉树我们需要得知root.left 与 root.right是否为对称的
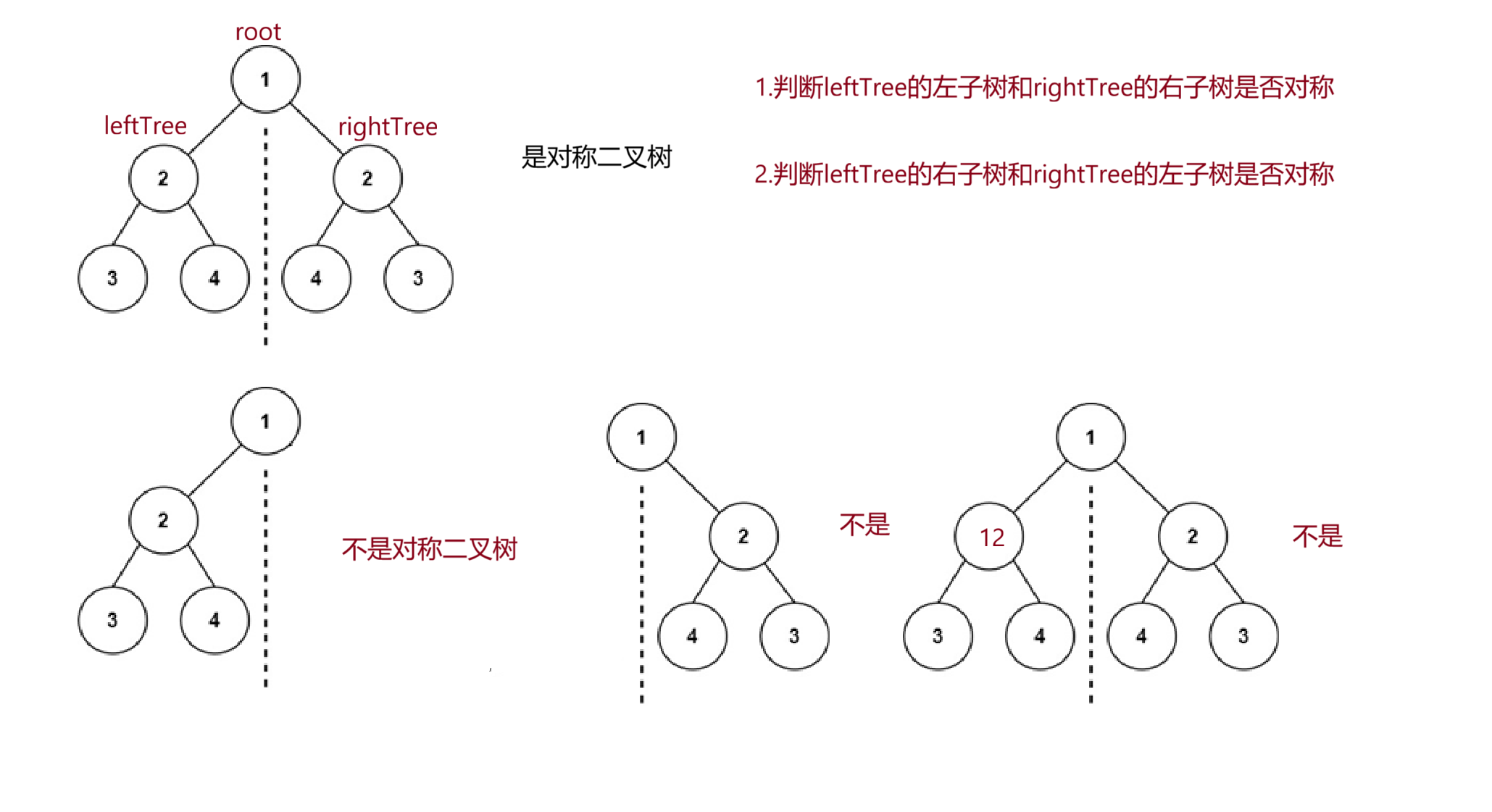
首先我们可以先写一个专门判断二叉树的左子树leftTree与右子树rightTree是否为对称的方法
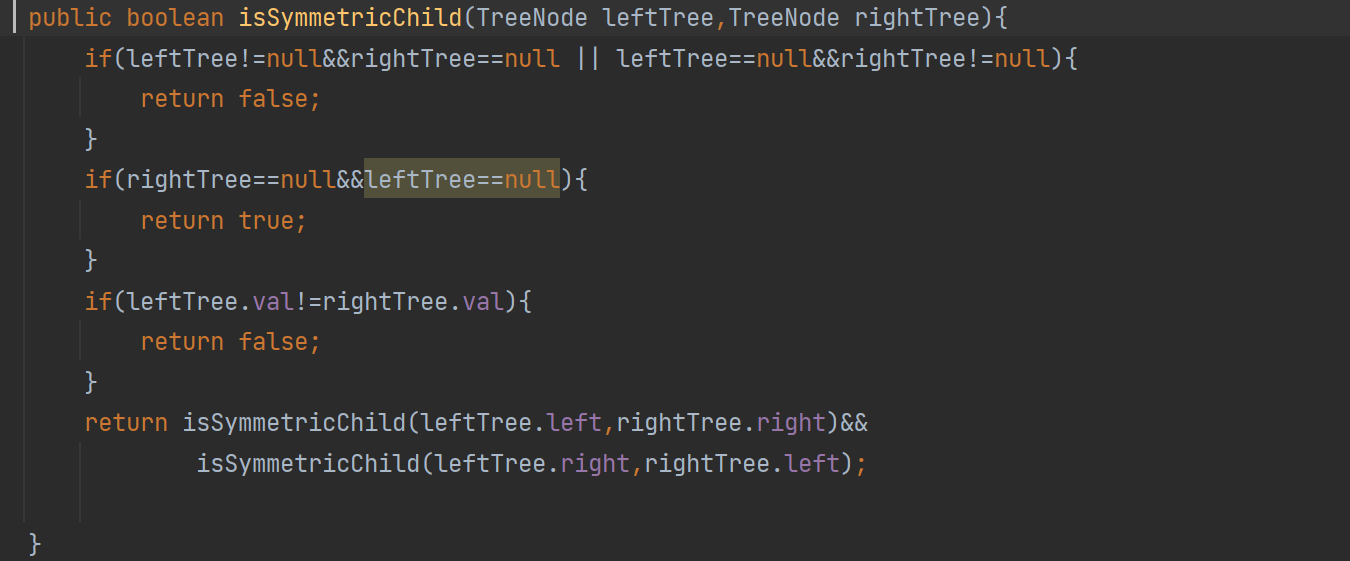
之后我们直接调用这个方法，就可以完成代码
public boolean isSymmetric(TreeNode root) {if(root==null){return true;}return isSymmetricChild(root.left, root.right);}public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){if(leftTree!=null&&rightTree==null || leftTree==null&&rightTree!=null){return false;}if(rightTree==null&&leftTree==null){return true;}if(leftTree.val!=rightTree.val){return false;}return isSymmetricChild(leftTree.left,rightTree.right)&&isSymmetricChild(leftTree.right,rightTree.left);}
- 平衡二叉树，什么是平衡二叉树？平衡二叉树是指每一个节点的左子树高度与右子树的高度的差值<=1 ，注意是每一个结点
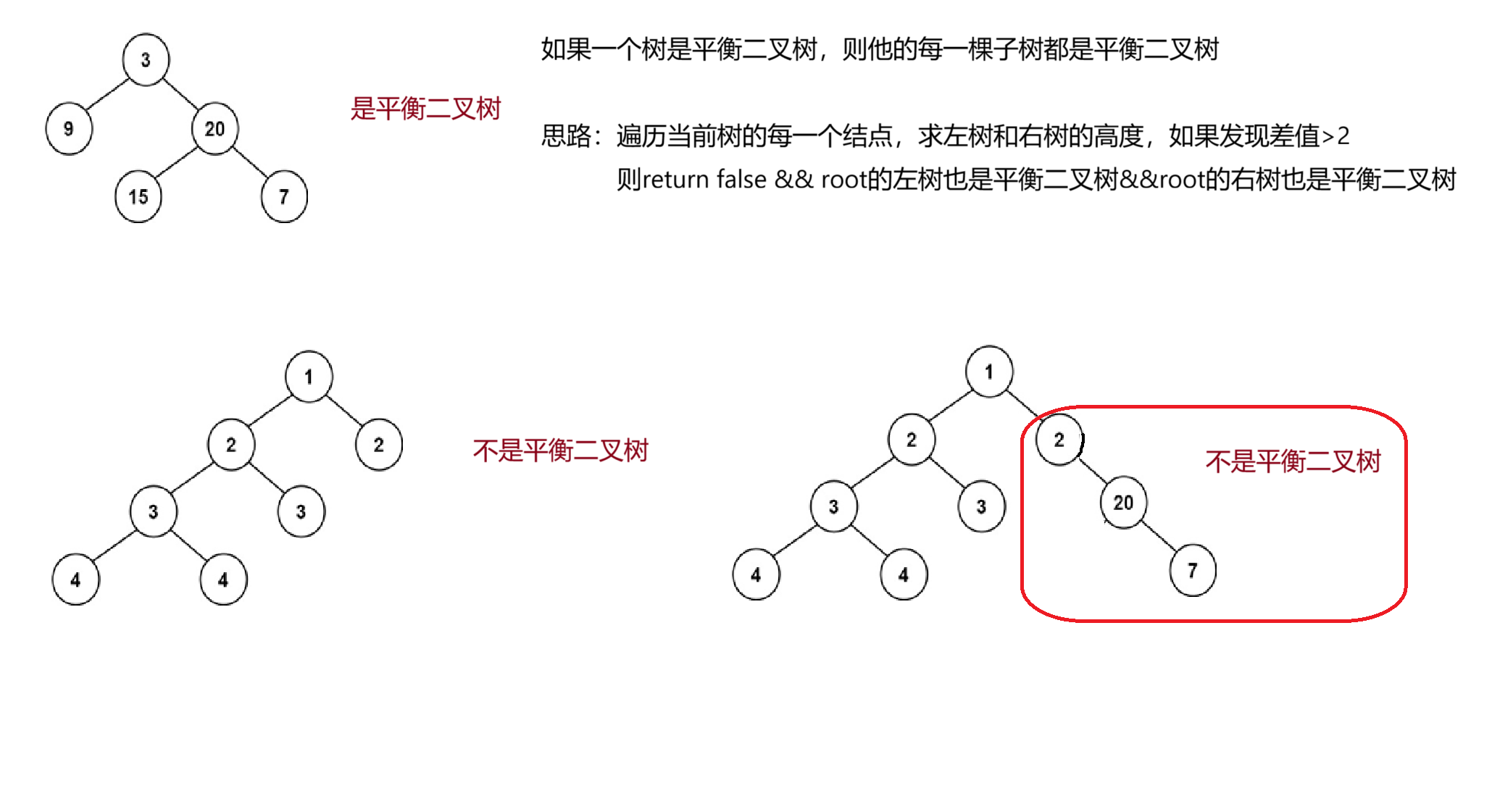在上篇博客的学习中，我们已经学会了如何求树的高度
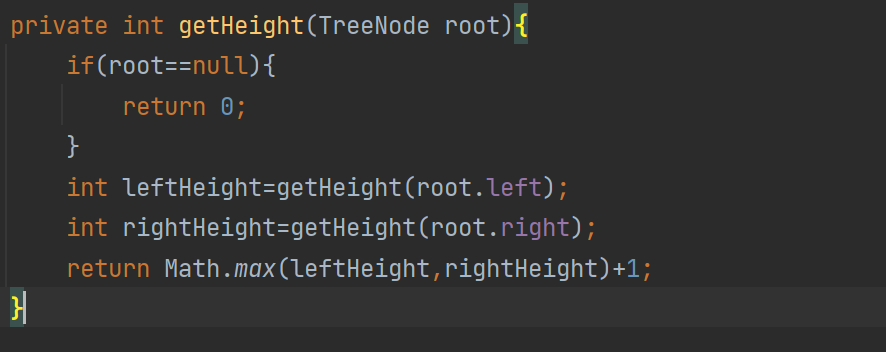我们只需要在这个基础上完善代码即可
class Solution {public boolean isBalanced(TreeNode root) {if(root==null){return true;}int leftHeight=getHeight(root.left);int rightHeight=getHeight(root.right);return Math.abs(leftHeight-rightHeight)<=1&&isBalanced(root.left)&&isBalanced(root.right);}private int getHeight(TreeNode root){if(root==null){return 0;}int leftHeight=getHeight(root.left);int rightHeight=getHeight(root.right);return Math.max(leftHeight,rightHeight)+1;}
}
紧贴我们的思路！！
下面我们关注一下这个代码的时间复杂度，时间复杂度为O（N^2），因为每一次求树的高度都要重新从头遍历，我们该如何让这个代码的实现达到时间复杂度为O（N）呢！？ 也就是只遍历一次树即可
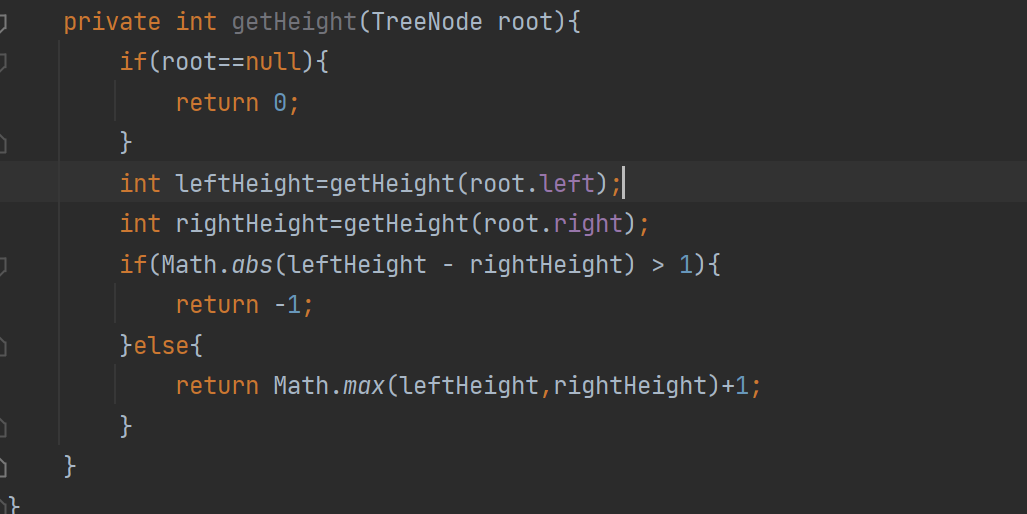我们在return前增加了一串代码，如果左树右树高度之差大于1了，那么return -1，这里我们需要接收一下-1
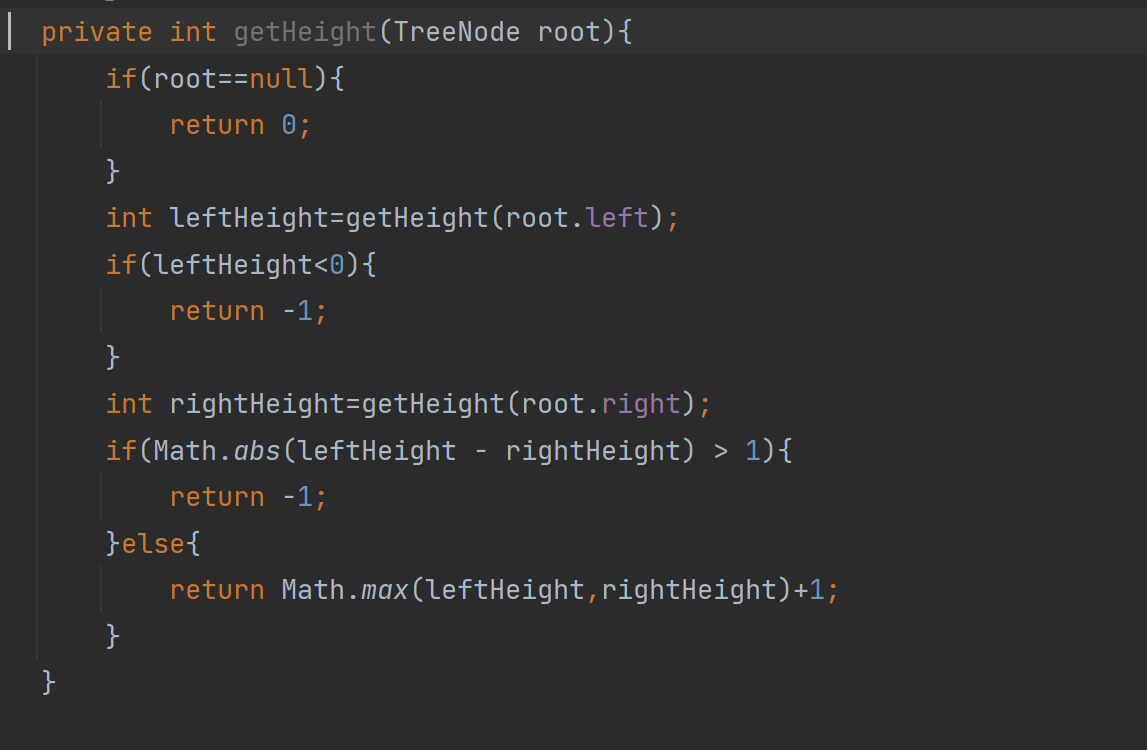如果左树拿到了return的值且为-1，那么我直接让左树返回-1
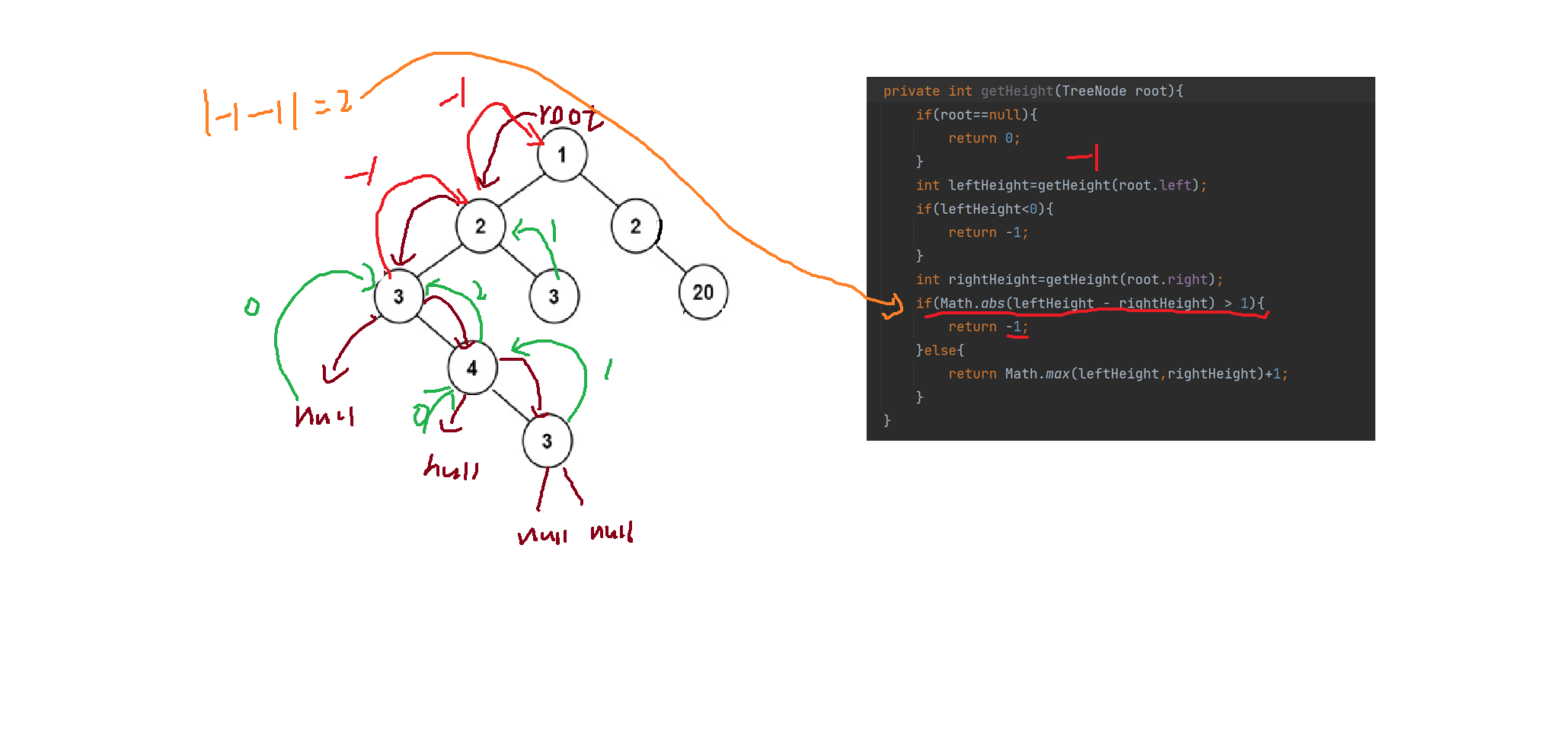
这里有的小伙伴就会觉得代码已经完善了，可是我们少考虑了一种情况，如果rightHeight也为负数，leftHeight==0，那么0-（-1）=1，这个代码就有问题了！！
class Solution {public boolean isBalanced(TreeNode root) {if(root==null){return true;}return getHeight(root)>0;}private int getHeight(TreeNode root){if(root==null){return 0;}int leftHeight=getHeight(root.left);if(leftHeight<0){return -1;}int rightHeight=getHeight(root.right);if(Math.abs(leftHeight - rightHeight) > 1 || rightHeight<0){return -1;}else{return Math.max(leftHeight,rightHeight)+1;}}
}
当然这里的getHeight方法也可以这样写
private int getHeight(TreeNode root){if(root==null){return 0;}int leftHeight=getHeight(root.left);if(leftHeight<0){return -1;}int rightHeight=getHeight(root.right);if(Math.abs(leftHeight - rightHeight) <2&& rightHeight >= 0){return Math.max(leftHeight,rightHeight)+1;}else{return -1;}}
注意 “||”和“&&”区别
- 二叉搜索树与双向链表，这里我们的目的是输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。
首先什么二叉搜索树？二叉搜索树就是 左子树值<根结点值<右子树值
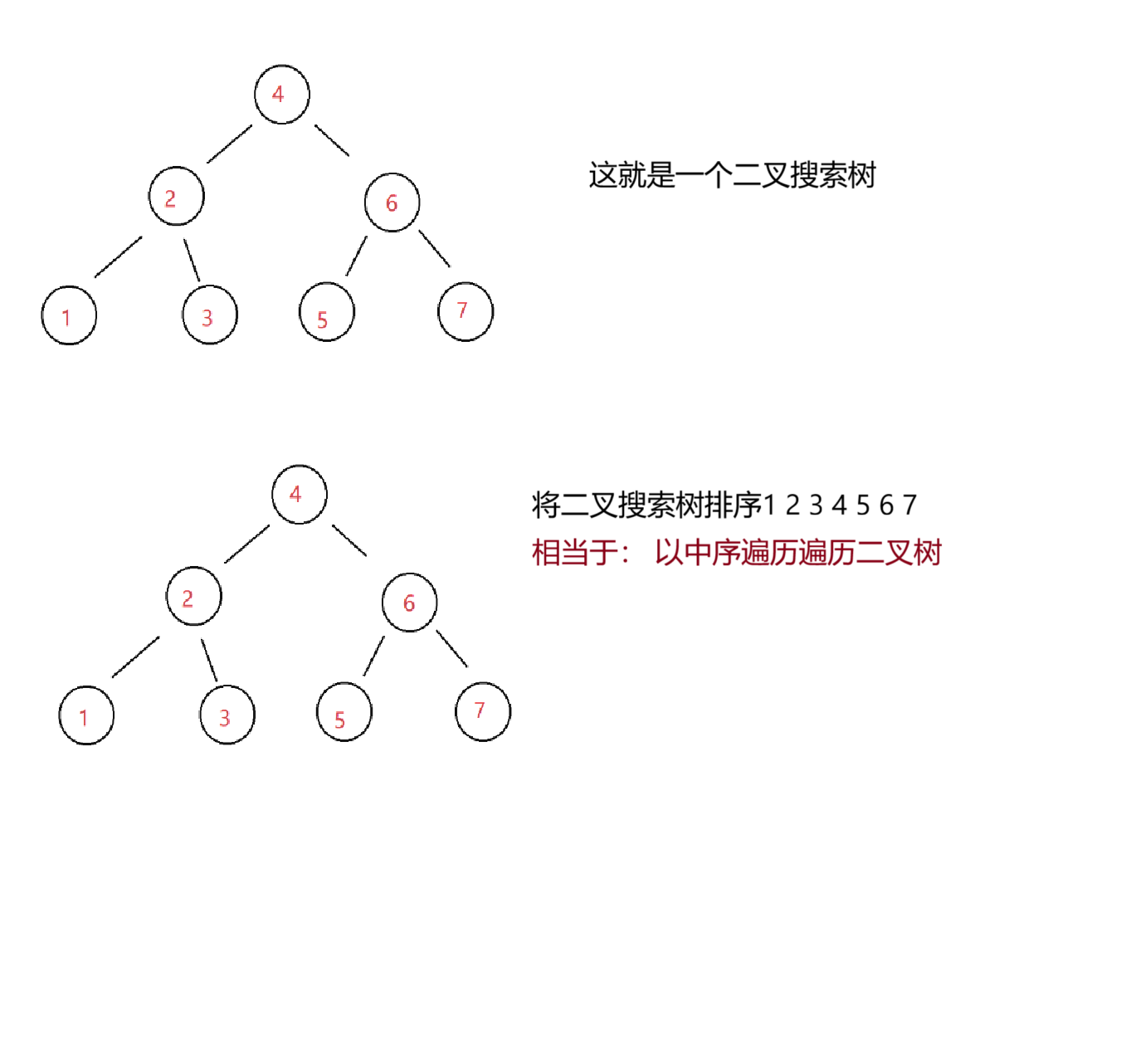我们先完成中序遍历这个方法
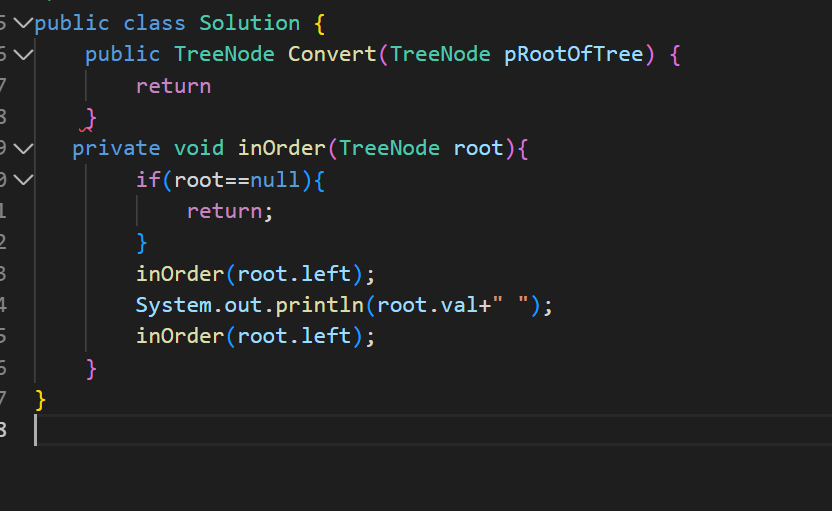下面我们看如何将二叉树转换为双向链表
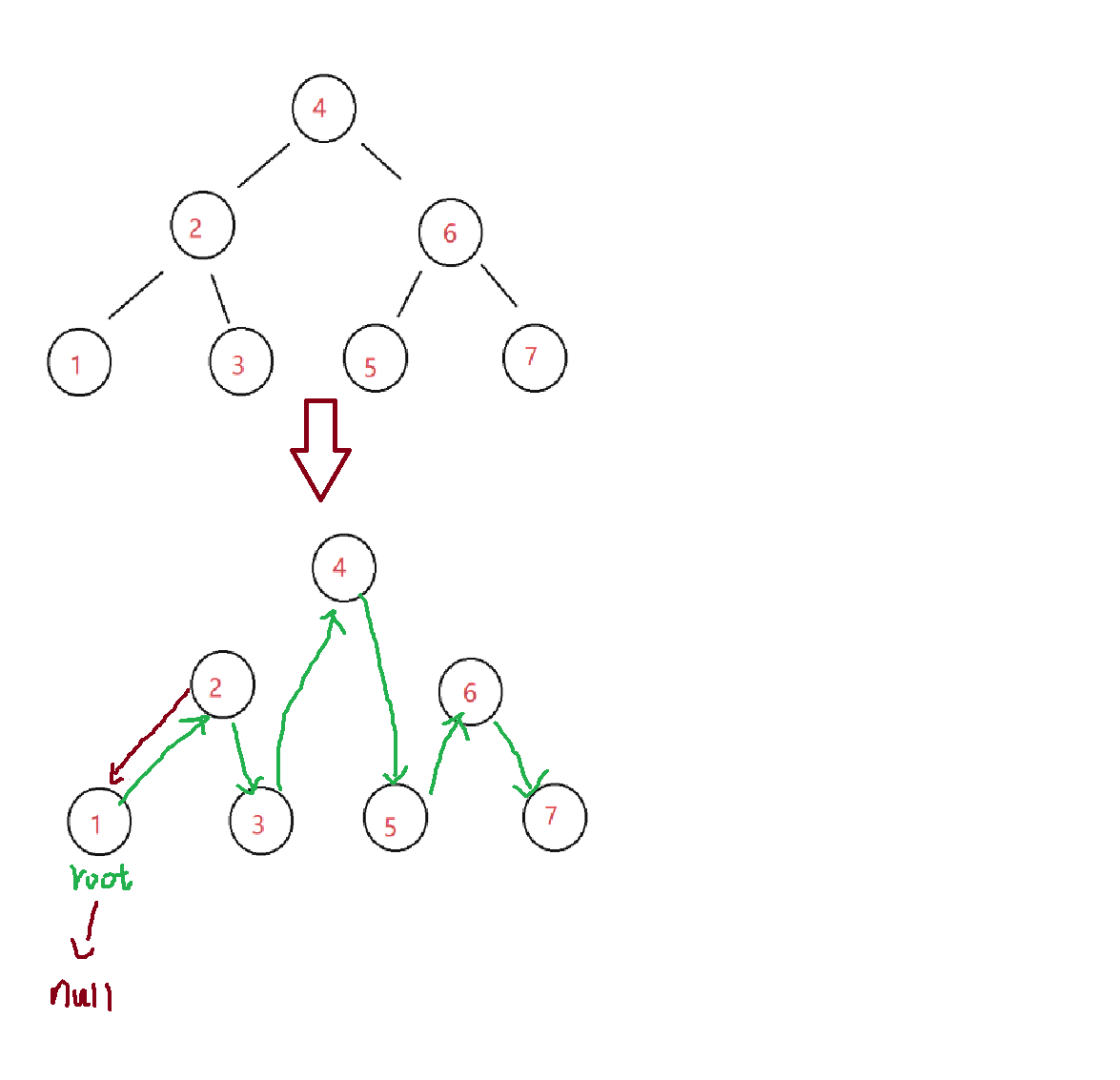
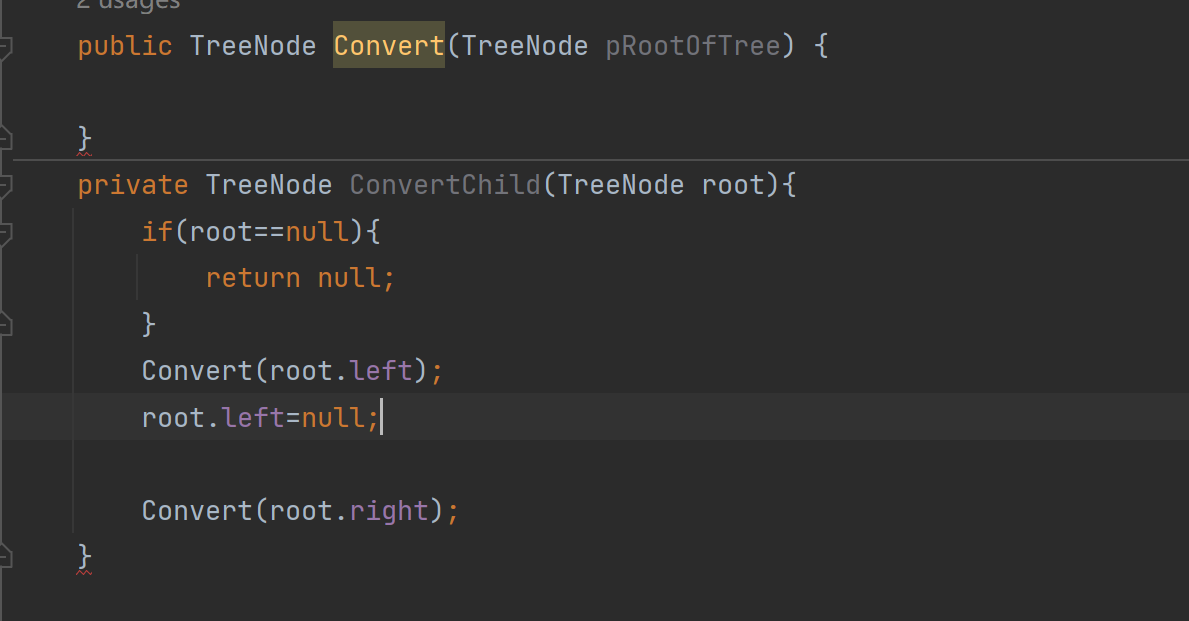
这样写的话，经历每一次循环root.left永远为null，可见不行！
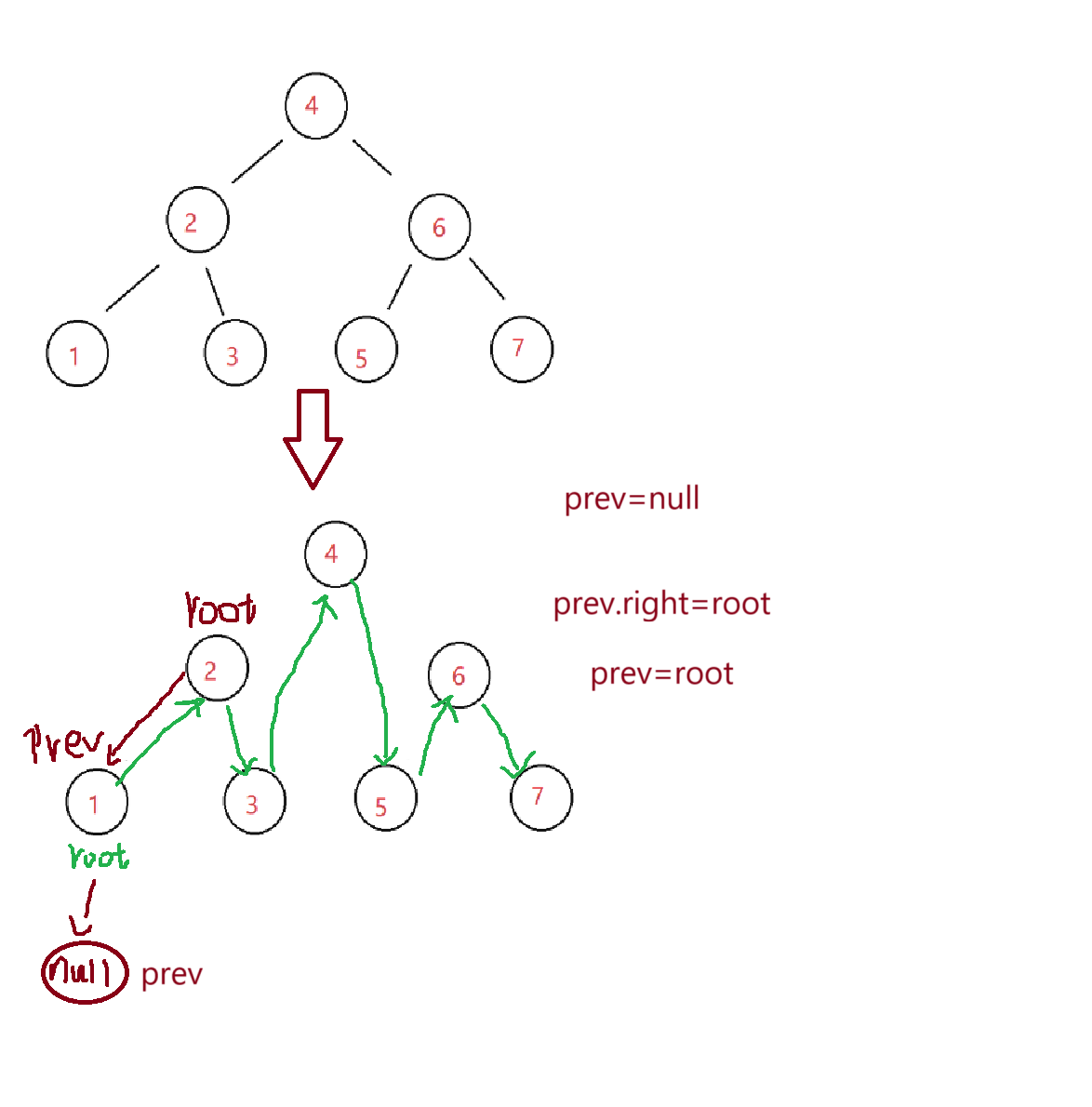
利用一个prev的变量，将prev的right域指向循环后的root，然后让prev指向root，顺序不能变
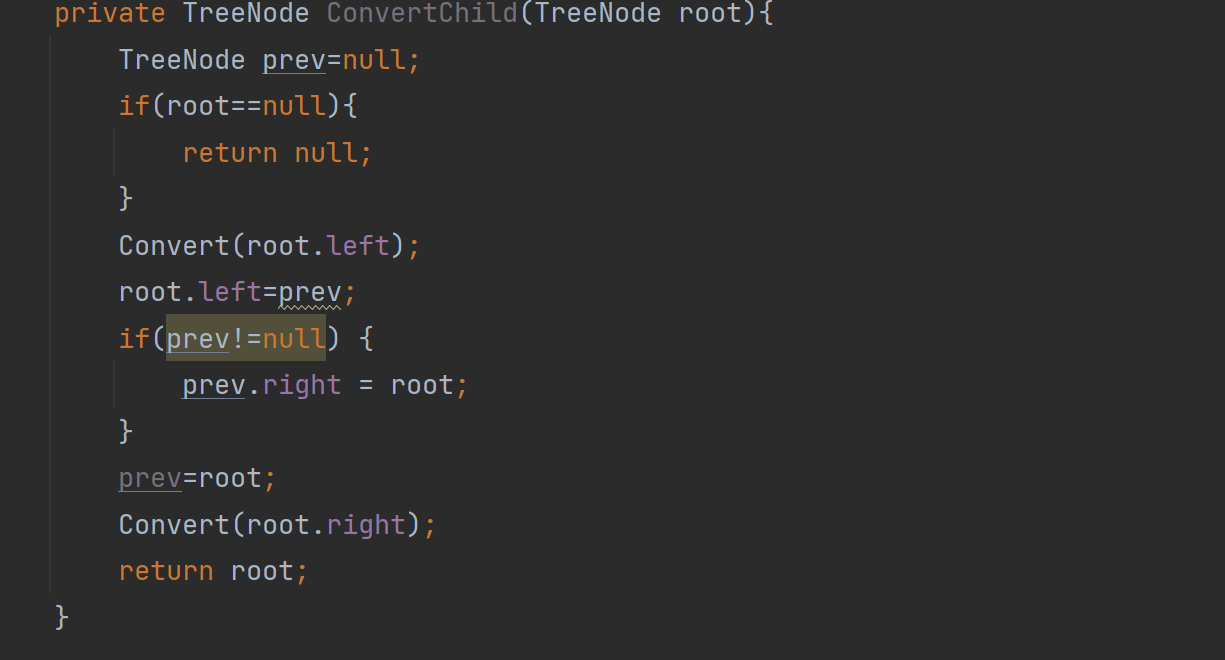这里还要注意prev如果为null的话就没有right域，我们再看这个代码是否有问题呢？
这里注意！！prev域不能定义在方法里，每次递归这个方法会重新给prev赋值为null
我们的要求是返回链表的头节点，这里我们传入 pRootOfTree最后它的位置仍然在根结点上，所以我们要定义一个头指针head，让head走到最左边！下面我们完善代码
public TreeNode Convert(TreeNode pRootOfTree) {if (pRootOfTree == null) return null;ConvertChild(pRootOfTree);TreeNode head = pRootOfTree;while (head.left != null) {head = head.left;}return head;}private TreeNode prev=null;private void ConvertChild(TreeNode root) {if (root == null) {return ;}ConvertChild(root.left);root.left = prev;if (prev != null) {prev.right = root;}prev = root;ConvertChild(root.right);}这样我们的代码才完善！
-
二叉树的构建和遍历，本题的意思是输入 ABC##DE#G##F### 其中“#”表示的是空格，空格代表空树，建立后再进行中序遍历
我们可以先搭框架，先完成中序遍历的方式
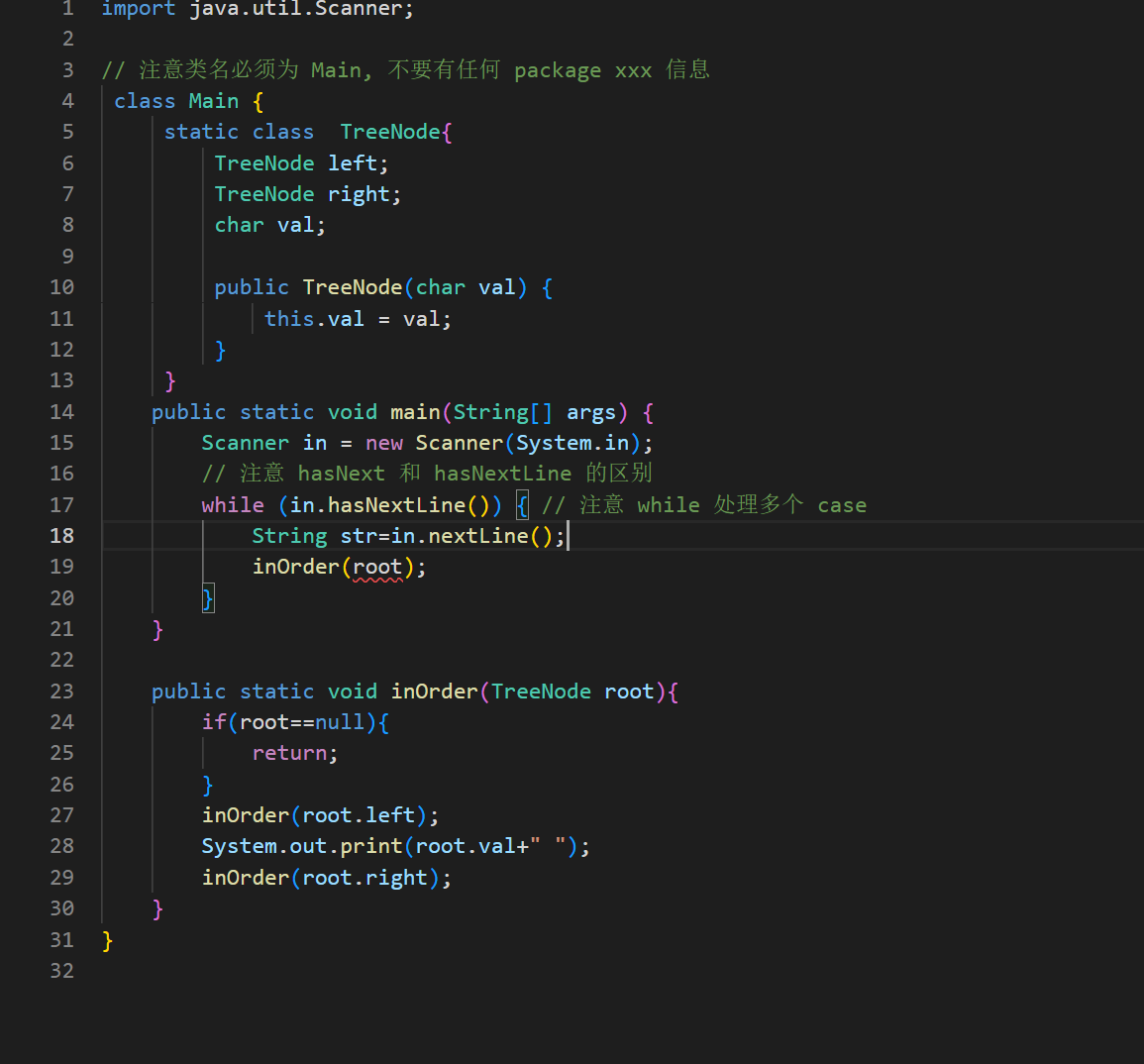下面我们看看应该如何去创建这棵树
我们可以遍历传入的字符串，如果遇到非‘#’那么就创造一个新的节点，i++，如果遇到‘#’那么直接让i++即可
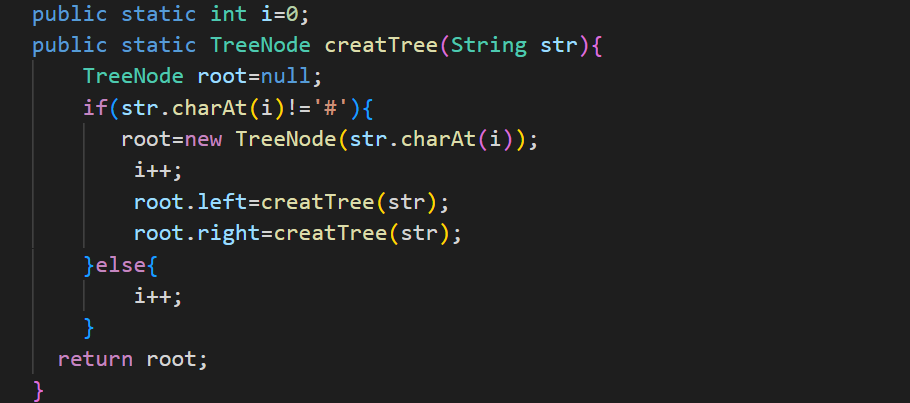我们这里让i作为一个静态的成员变量，i 不能为局部变量，因为i的值是在改变的基础上继续变化的，当然静态的变量也有不好之处，如果传入的字符串太大则不行，所以这里可以不用static修饰但是调用方法时要用类的引用调用。
class Main {static class TreeNode{TreeNode left;TreeNode right;char val;public TreeNode(char val) {this.val = val;}}public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) {String str=in.nextLine();TreeNode root=creatTree(str);inOrder(root);}}public static int i=0;public static TreeNode creatTree(String str){TreeNode root=null;if(str.charAt(i)!='#'){root=new TreeNode(str.charAt(i));i++;root.left=creatTree(str);root.right=creatTree(str);}else{i++;}return root;}public static void inOrder(TreeNode root){if(root==null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}
}
这样这个方法就完成了
- 二叉树的层序遍历，题目中出现了我们之前遇到的二维数组，我们要以二维数组的方式进行输出，其中每一行的一维数组代表二叉树的各个元素，在完成这道题之前，我们先来看看普通的层序遍历应该如何去做呢？
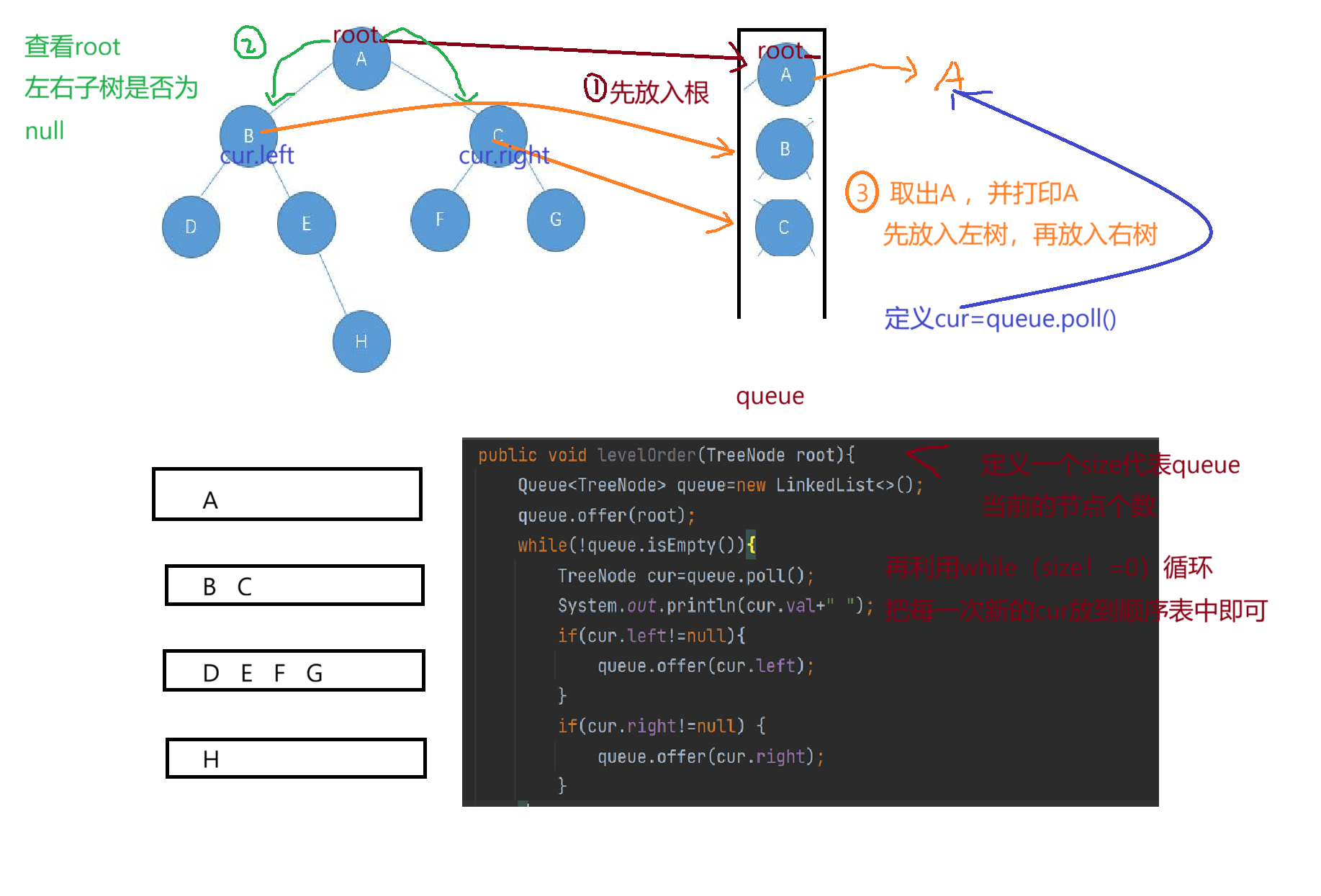
对于层序遍历，我们可以不使用递归来实现，我们需要引入队列这个数据结构去实现我们的操作
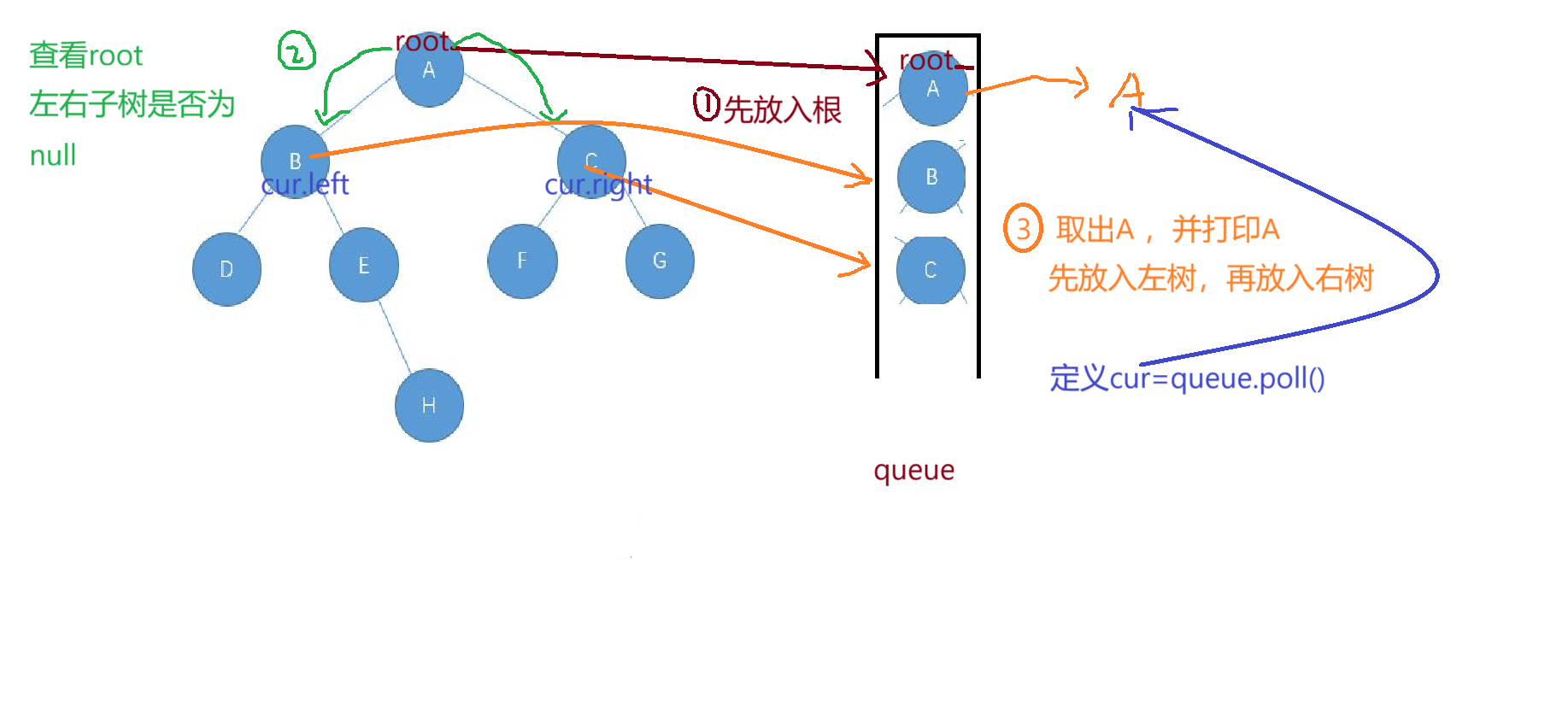
我们可以根据图完成代码
public void levelOrder(TreeNode root){Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){TreeNode cur=queue.poll();System.out.println(cur.val+" ");if(cur.left!=null){queue.offer(cur.left);}if(cur.right!=null) {queue.offer(cur.right);}}}
只要队列不为空，我就继续放，为空后我的二叉树元素就被全部打印了！
下面我们来看这道题，与上述不一样的是，我们要返回一个二维数组，下面我们思考如何结合二维数组完成二叉树的层序遍历？二维数组是由一个个一维数组组成，我们只需要把每一层元素放到一个一维数组中即可
我们直接来实现一下
public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ret=new ArrayList<>();if(root==null){return ret;}Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){List<Integer> list=new ArrayList<>();int size=queue.size();while(size!=0){TreeNode cur=queue.poll();list.add(cur.val);if(cur.left!=null){queue.offer(cur.left);}if(cur.right!=null) {queue.offer(cur.right);}size--;}ret.add(list);}return ret;}
这里注意，每次的顺序表都要放在size循环中，每次cur=queue.poll()也要放入循环之中，因为如果在外就取不到值了
- 判断一棵树是不是完全二叉树
我们思考什么是完全二叉树？
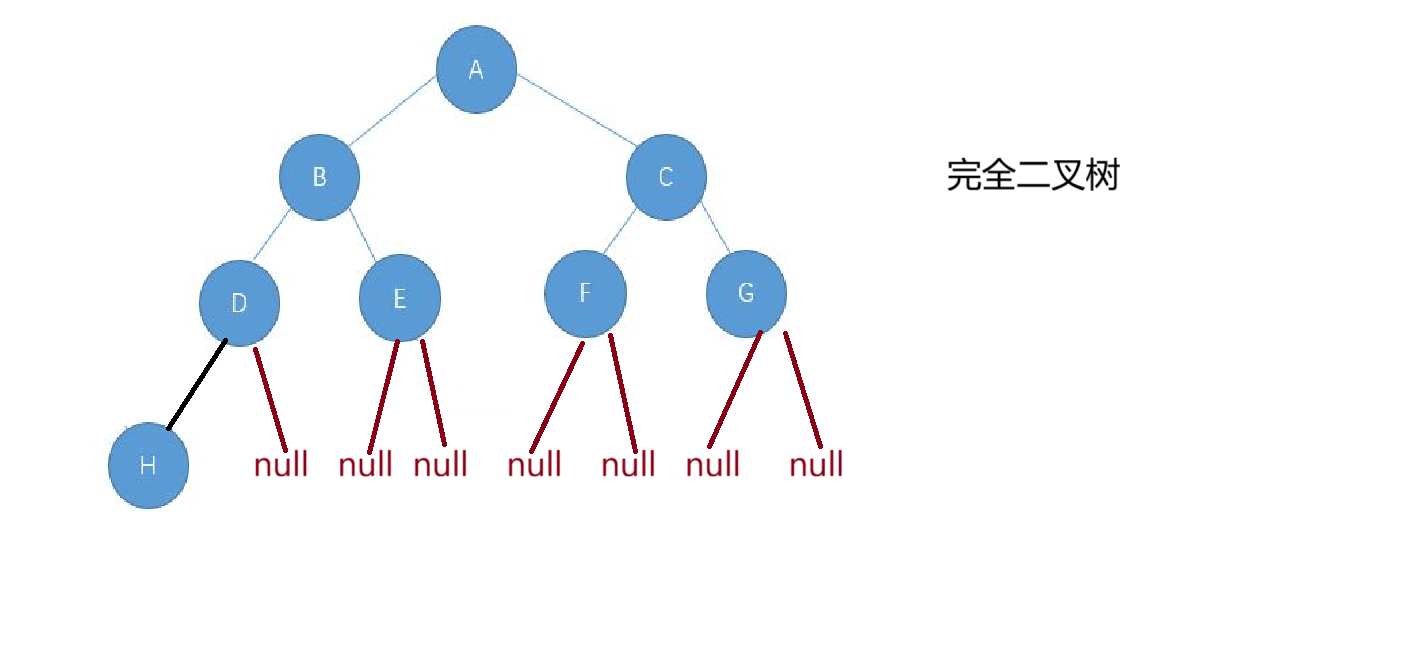
这就是一个完全二叉树，我们还是利用队列来实现，那么应该如何实现呢？
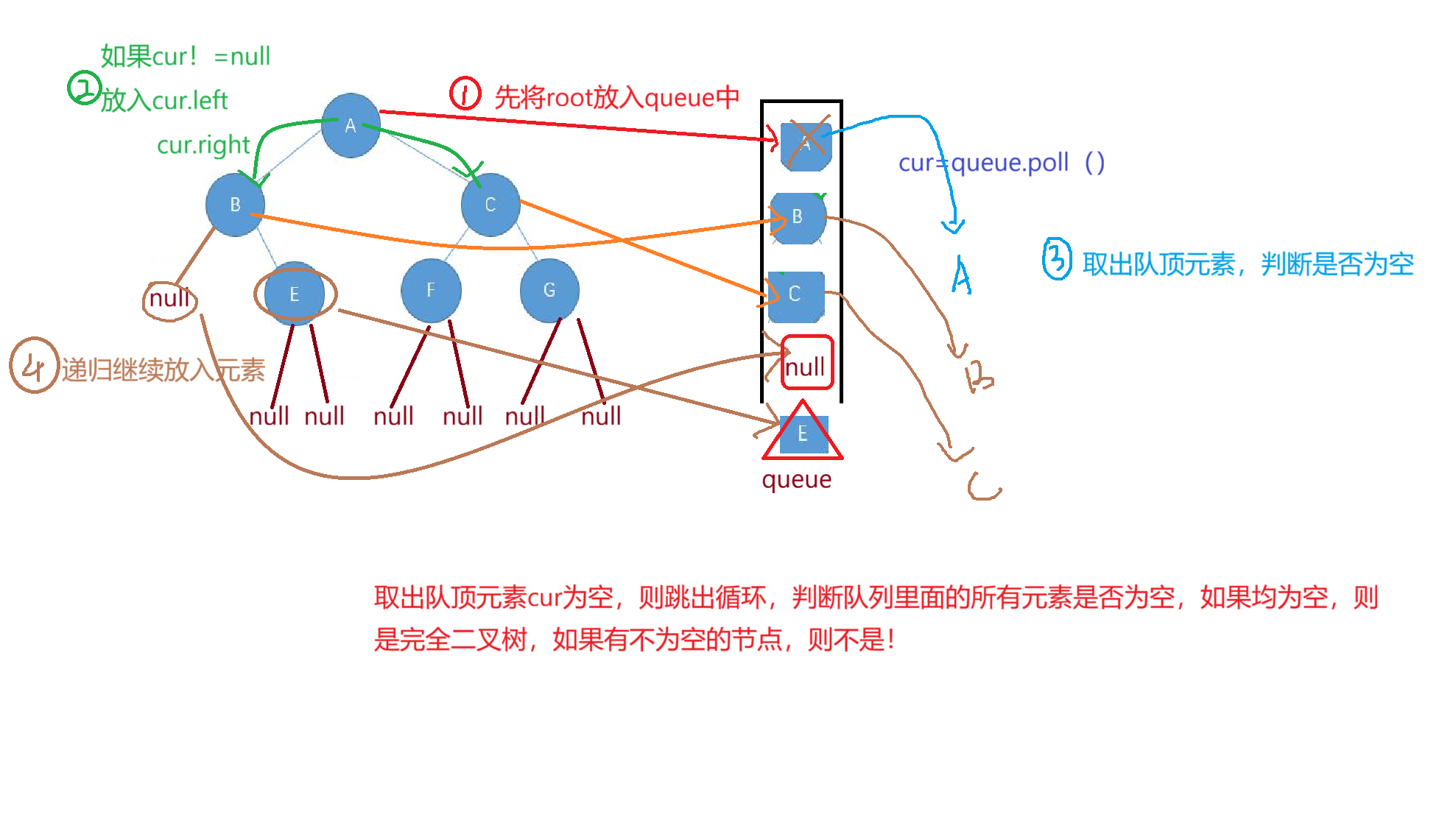
我们来完善一下代码
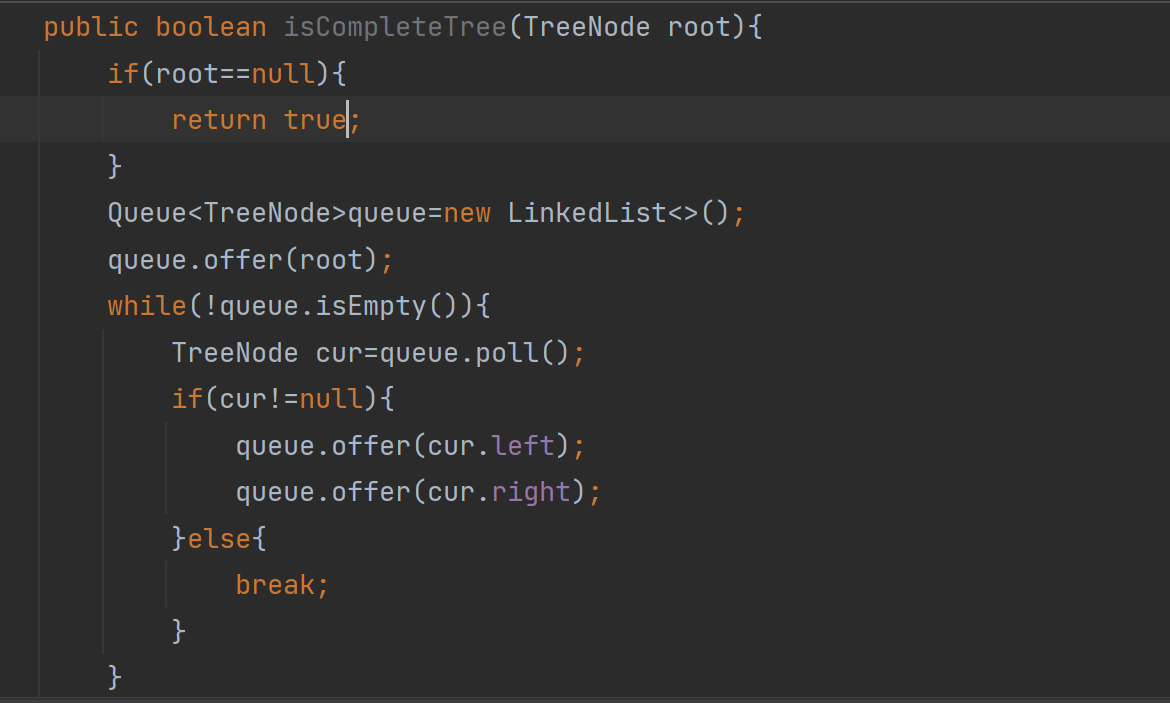
首先这里与我们层序遍历二叉树很相似，我们只要碰见null就跳出循环
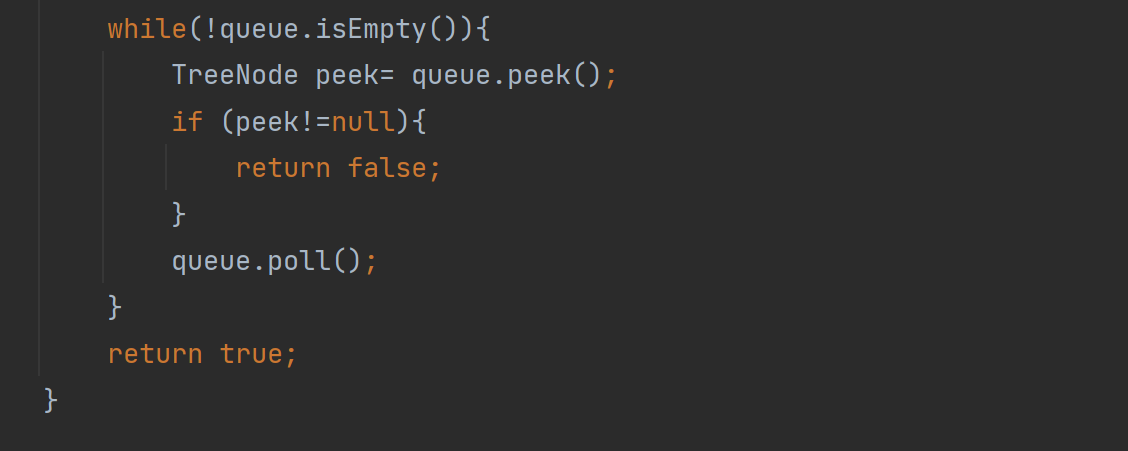跳出循环后，我们执行这部分代码，判断当前队列是否全为null，这样我们的代码就完成了
public boolean isCompleteTree(TreeNode root){if(root==null){return true;}Queue<TreeNode>queue=new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){TreeNode cur=queue.poll();if(cur!=null){queue.offer(cur.left);queue.offer(cur.right);}else{break;}}while(!queue.isEmpty()){TreeNode peek= queue.peek();if (peek!=null){return false;}queue.poll();}return true;}
以上就是本篇博客的全部练习，所有代码在这🌹
3. 结语
以上就是本文主要的内容，我们主要实现了二叉树的很多练习题，接下来还会有一部分练习题，以及顺序表实现二叉树的知识，请大家敬请期待！！有不明白的地方可以留言小编会回复，希望读者们多提建议，小编会改正，共同进步！谢谢大家。🌹🌹🌹