当前位置：首页 > news >正文

流匹配动作生成

news 2025/11/5 15:30:08

基于流匹配（Flow Matching）的动作生成

1. 核心思想

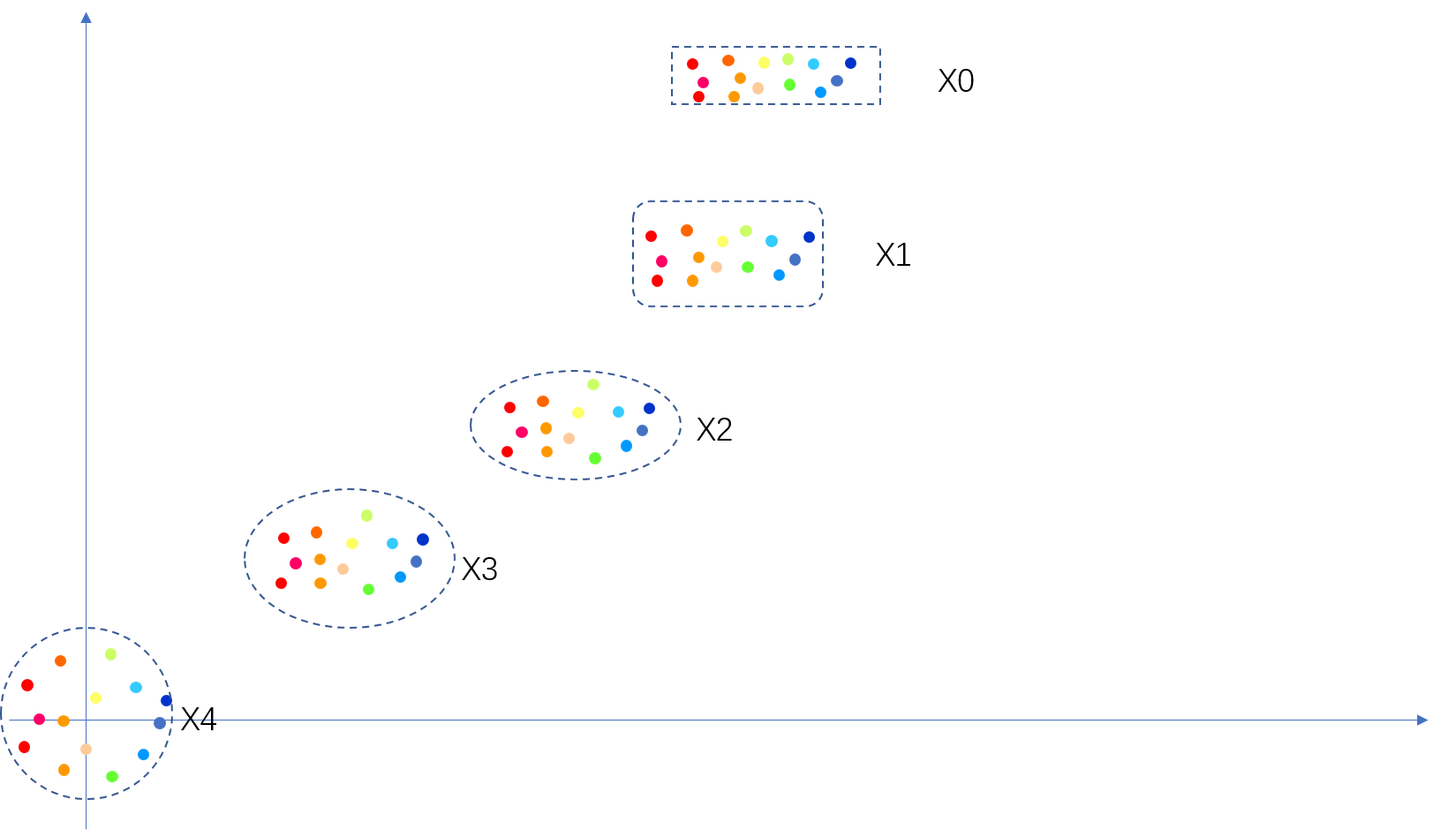
传统的方法（如行为克隆）直接学习一个确定性策略 $\pi(o)$ 或一个条件分布 $P (A ∣ o)$ 。而流匹配方法采用了一种生成式模型的思路，通过一个速度场来刻画从噪声分布到目标动作分布的连续变换过程, 如图中从x4->x0，最上边是动作空间X0，坐标原点是高斯噪声空间X4。
在这里插入图片描述

2. 数学框架：定义路径

首先，需要定义一条连接噪声空间和真实动作空间的路径。

起点（ $t = 0$ ）：一个容易采样的简单分布，通常是标准高斯分布。
- 动作状态： $A0∼p0=N(0,I)A^0 \sim p_0 = \mathcal{N}(0, I)$
终点（ $t = 1$ ）：我们想要得到的真实、复杂的动作分布。
- 动作状态： $A1∼pdataA^1 \sim p_{\text{data}}$ （即来自专家数据的真实动作块 $A$ ）
路径（ $0 < t < 1$ ）：在起点和终点之间，我们定义一条连续的路径。对于任意时间 $t$ ，都有一个对应的动作状态 $A^t$ 。最简单的是直线路径：
- $At=(1−t)⋅A0+t⋅A1A^t = (1 - t) \cdot A^0 + t \cdot A^1$
- 当 $t = 0$ 时， $A^0$ 就是起点噪声
- 当 $t = 1$ 时， $A^1$ 就是终点真实动作

3. 关键概念：速度场（Velocity Field）

速度场 $v(A^t, o, t)$ 是流匹配方法的核心。

直观理解：想象 $A^t$ 是时刻 $t$ 的一个粒子。这个粒子要从噪声 $A^0$ 运动到目标动作 $A^1$ 。速度场 $v$ 就定义了这个粒子在每一个时间点 $t$ 、每一个位置 $A^t$ 上，应该朝着哪个方向、以多快的速度运动。
数学定义：速度场是路径 $A^t$ 对时间 $t$ 的导数，即瞬时变化率。
- $v(At,o,t)=dAtdtv(A^t, o, t) = \frac{dA^t}{dt}$

对于我们上面定义的直线路径 $A^t = (1-t)A^0 + tA^1$ ，我们可以计算其速度场：

$v(At,o,t)=d[(1−t)A0+tA1]dt=A1−A0v(A^t, o, t) = \frac{d[(1-t)A^0 + tA^1]}{dt} = A^1 - A^0$

这个结果非常重要：它意味着，对于一条已知的、连接 $A^0$ 和 $A^1$ 的路径，其真实的速度场就是终点和起点之间的向量差 $A^1 - A^0)$ 。

4. 训练目标：学习速度场

在推理时，我们不知道真实的 $A^1$ （那就是我们要生成的目标）。所以，我们需要一个神经网络 $vθv_\theta$ 来学习逼近这个真实的速度场。

训练数据：我们拥有专家数据对 $(o, A)$ ，其中 $A$ 就是真实的 $A^1$
训练过程：
1. 随机采样一个专家数据对 $(o, A)$
2. 从高斯分布中采样一个噪声起点 $A0∼N(0,I)A^0 \sim \mathcal{N}(0, I)$
3. 随机采样一个时间点 $\sim \text{Uniform}(0, 1)$
4. 根据路径公式（如直线路径）计算 $t$ 时刻的中间状态： $At=(1−t)A0+t⋅AA^t = (1-t)A^0 + t \cdot A$
5. 计算真实的速度场： $vtrue=A−A0v_{\text{true}} = A - A^0$ （根据上面的推导）
6. 让神经网络 $vθv_\theta$ ，以 $A^t, o, t)$ 为输入，预测速度场 $vpred=vθ(At,o,t)v_{\text{pred}} = v_\theta(A^t, o, t)$
7. 最小化预测值与真实值之间的差距（如 L2 损失）：

$L(θ)=E[∥vθ(At,o,t)−(A−A0)∥2]\mathcal{L}(\theta) = \mathbb{E}[ \| v_\theta(A^t, o, t) - (A - A^0) \|^2 ]$

通过这个简单的损失函数，神经网络学会了在给定观测 $o$ 下，如何将任意一个中间状态 $A^t$ 推向下一个"更接近"真实专家动作 $A$ 的状态。

5. 推理（生成）过程：从噪声迭代到动作

训练好网络后，我们就可以进行推理，从噪声"流式"地生成动作：

初始化：从高斯分布采样一个随机噪声 $A0∼N(0,I)A^0 \sim \mathcal{N}(0, I)$
迭代求解（例如使用欧拉法）：
- 将时间区间 $[0, 1]$ 离散成 $N$ 个小步（如 $\ldots, 1.0$ ）
- For $k = 0$ to $N - 1$ :
  - 当前时间 $t_k = k / N$ ，当前状态是 $A^{t_k}$
  - 将 $A^{t_k}, o, t_k)$ 输入神经网络 $vθv_\theta$ ，得到预测的速度 $vpredv_{\text{pred}}$
  - 更新状态（向前走一小步）：
  $Atk+1=Atk+1N⋅vpredA^{t_{k+1}} = A^{t_k} + \frac{1}{N} \cdot v_{\text{pred}}$
- End For
输出：最终的状态 $A^{t=1}$ 就是我们生成的动作 $A$