当前位置：首页 > news >正文

Similarity Between Binary Vectors｜二元向量的相似性

news 2025/11/5 15:22:46

-----------------------------------------------------------------------------------------------

这是我在我的网站中截取的文章，有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn，这里还有很多有关计算机的知识，欢迎进行留言或者来我的网站进行留言！！！

----------------------------------------------------------------------------------------------

一、引言

在数据分析和机器学习中，我们经常需要比较不同对象之间的相似性（similarity）。
对于数值型数据，可以使用欧氏距离（Euclidean Distance）或余弦相似度（Cosine Similarity）来衡量；
但当对象的属性仅由0和1组成时（即二元向量 Binary Vector），传统的距离计算方法往往不再适用。

这种二元特征在现实中十分常见，例如：

文本挖掘中，词是否出现（1表示出现，0表示未出现）；
医疗数据中，患者是否具备某种症状；
推荐系统中，用户是否点击或购买某项商品。

在这些情况下，我们希望通过一种合理的方式，计算两个二元向量之间的相似度，以判断它们在特征表现上的一致性或差异性。
常见的两种计算方法是：

Simple Matching Coefficient (SMC) —— 简单匹配系数；
Jaccard Coefficient —— 杰卡德相似系数。

二者都基于特征维度上的“匹配”与“不匹配”统计来衡量对象间的相似程度，
但它们在处理“零匹配”时的权重不同，导致适用场景也有所区别。

二、二元向量的基本定义

在讨论 SMC 和 Jaccard 系数之前，我们需要明确如何表示二元向量之间的关系。
假设有两个对象 x 和 y，它们都由若干个二元属性组成（即每个属性的取值要么是0，要么是1）。
为了计算它们之间的相似度，我们可以统计它们在各个维度上出现的组合情况。

下表展示了常用的四种统计量定义：

记号	含义说明
f01	属性中，x = 0 且 y = 1 的个数
f10	属性中，x = 1 且 y = 0 的个数
f00	属性中，x = 0 且 y = 0 的个数
f11	属性中，x = 1 且 y = 1 的个数

通过这四个数值，我们就能完整描述两个二元向量在特征维度上的匹配与差异情况。
其中：

f11 代表两个向量在同一位置都为1的次数，即“共同存在”的特征；
f00 表示两个向量都为0的次数，即“共同缺失”的特征；
而 f10 和 f01 则体现了它们的不一致部分。

这些统计值是计算 SMC 和 Jaccard 的基础，
不同的相似度系数正是通过对这些数量的不同组合来定义对象间的“接近程度”。

三、SMC与Jaccard系数的计算公式

在了解了 f01f01、f10f10、f00f00、f11f11 四个统计值之后，我们可以正式定义两种常见的相似度度量：SMC（Simple Matching Coefficient） 和 Jaccard Coefficient（杰卡德系数）。

1. Simple Matching Coefficient（SMC）

SMC 衡量的是两个二元向量中匹配（相同）的比例。
它同时考虑：

两个向量都为 1 的情况（共同存在）；
两个向量都为 0 的情况（共同缺失）。

其计算公式为：

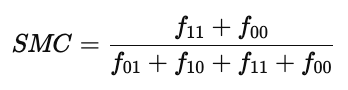
分子部分 f11+f00 表示两者在所有属性中“相同”的次数，
分母则是所有属性的总数。
因此，SMC 反映了两个对象在所有维度上整体的一致性。

2. Jaccard Coefficient（杰卡德系数）

与 SMC 不同，Jaccard 系数只关注特征的共同存在，而忽略了双方都为0的情况。
它的思想是：如果某个特征在两个对象中都未出现，那么这一维度不应增加它们的相似性。

其计算公式为：

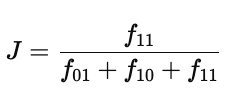
分子 f11 代表两个对象都为 1 的属性个数；
分母则表示至少有一个对象为 1 的总属性数。
因此，Jaccard 更适用于强调“共有特征”的场景，比如标签匹配、关键词共现分析等。

两者的区别可以简单总结为：

SMC 适用于需要整体一致性衡量的情况，既重视“都为1”，也重视“都为0”；
Jaccard 适用于只关注共同出现特征的情况，忽略共同缺失部分。

四、概念差异与理解

虽然 SMC 与 Jaccard 都用于衡量二元向量之间的相似性，但它们在概念上存在根本的区别。
理解这种差异有助于我们根据实际数据类型选择合适的度量方法。

1. SMC 的特点

SMC（Simple Matching Coefficient） 同时考虑匹配与不匹配的情况。
它把两个对象都为1（共同存在）和都为0（共同缺失）视为同等重要的“相似”。

这种方法的优点是：

能反映总体的一致性；
适合特征取值均衡的场景，例如二元变量0和1出现频率接近时。

然而，它的缺点在于：

如果样本中有大量“0”的特征（即缺失的情况很多），这些“共同为0”会拉高相似度，从而掩盖了真实的差异。

2. Jaccard 的特点

Jaccard Coefficient 只考虑两个对象共同为1的特征，
忽略双方都为0的部分。
它关注的是“有的相似”，而非“都没有的相似”。

这使得 Jaccard 特别适用于：

稀疏数据（例如标签、关键词、症状等出现频率低的场景）；
强调“共有特征”的任务，如文档相似度、图像标签相似度、用户兴趣匹配。

因此，Jaccard 的值往往比 SMC 小，但更能反映对象之间的有效共同性。

3. 举例理解

如果我们比较两个样本，它们在十个属性中：

有八个都为0；
只有两个不同；

那么：

SMC 可能会给出较高的相似度，因为它认为8个共同的0是“匹配”；
Jaccard 则只考虑那两个非零特征的交集，更关注“共同出现”的部分。

这种差异正是两者在衡量逻辑上的本质区别。

五、实际计算示例

为了更直观地理解两种相似度系数的区别，我们可以通过一个二元向量的实际例子来说明。
下图展示了两个对象 xx 与 yy 的二元属性，以及对应的计算过程：

1. 数据设定

假设我们有两个对象：

每个位置代表一个二元属性（0 或 1），表示该对象是否具备某一特征。

2. 统计匹配情况

根据定义，我们统计出以下四种组合：

组合	含义	数量
f01	x=0,y=1	2
f10	x=1,y=0	1
f00	x=0,y=0	7
f11	x=1,y=1	0

这些数值反映了两个对象在不同特征取值下的匹配情况。

3. 计算 SMC（Simple Matching Coefficient）

SMC 同时考虑“都为1”和“都为0”的匹配，因此它的计算公式为：

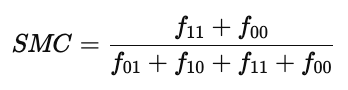
代入上表数值：

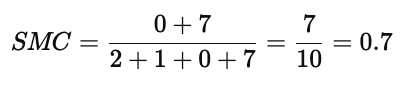
说明这两个对象在整体属性上有 70% 的匹配程度，即它们在“都为0”的特征上有较高的一致性。

4. 计算 Jaccard 系数

Jaccard 系数只考虑“都为1”的匹配（忽略都为0的部分），公式为：

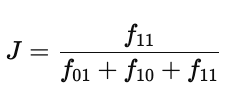
代入数据：

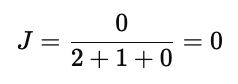
结果为 0，意味着在“存在的特征”上，两个对象完全没有交集。

5. 对比分析

SMC = 0.7：说明两个对象在整体特征上一致性较高；
Jaccard = 0：说明它们没有共享的“有效特征”（共同为1的情况）。

这正体现了两种度量的核心差异：

SMC 注重整体相似性（包括共同缺失），而 Jaccard 聚焦于共同存在的特征。

六、SMC 与 Jaccard 的应用场景

理解了计算过程之后，我们需要进一步思考：SMC 与 Jaccard 各自适用于什么类型的数据？
它们虽然都是衡量二元向量相似度的指标，但在“是否考虑共同为 0 的情况”上存在根本区别。
因此，在实际应用中，选择合适的度量方式非常关键。

1. SMC 的适用场景

SMC（Simple Matching Coefficient） 同时考虑“都为 1”与“都为 0”的匹配，因此在0 与 1 分布较均衡、
且“共同缺失”也有意义的场景中表现良好。

例如：

问卷调查分析：
如果两个受访者在多数问题上给出了相同答案（无论“是”还是“否”），SMC 能很好反映他们的总体一致性。
医疗诊断特征匹配：
患者若在多个症状上都“无表现”（即 0），这同样意味着相似。
工业状态监控：
两台设备若在大多数状态上都“正常运行”，其表现相似，应被视为一致。

SMC 的优势在于“全面”，它衡量的是总体特征上的一致性。
但在稀疏数据（多数为 0）中，它可能高估相似度。

2. Jaccard 的适用场景

Jaccard 系数只关注“共同为 1”的特征，忽略“共同为 0”的情况，因此更适合稀疏数据场景。

常见应用包括：

文本相似度计算：
在词袋模型（Bag-of-Words）中，一个词未同时出现在两个文档中并不代表它们相似，
而是它们共同出现的词更具意义。
推荐系统：
用户都没有购买的商品（0,0）不能说明兴趣一致，
而共同购买的商品（1,1）才是兴趣重合的体现。
标签或特征聚类：
当关注样本的“活跃特征”或“存在特征”时，Jaccard 比 SMC 更能反映实际关系。

Jaccard 的优势在于“专注”，它更适用于描述稀疏特征空间中的有效交集。

3. 两者对比总结

特征	SMC	Jaccard
是否考虑 (0,0) 匹配	是	否
适合的数据类型	特征分布均衡	稀疏数据
强调	全局一致性	共现特征
常见应用	问卷调查、状态监控	文本分析、推荐系统
优点	全面、简单	稀疏数据更准确
缺点	稀疏数据中易高估	忽略共同缺失信息