图解KMP算法
公共前后缀:直观的理解就是重复的子串。公共前后缀仅跟模式串自己有关
前缀集合:以字符串第一个字符开头的所有子串,比如A___
后缀集合:以字符串最后一个字符为末尾的所有子串,比如___B
注意:它们都不包含最后一个字符。
字符串: "ABABA"
前缀集合A__: "A", "AB", "ABA", "ABAB".
后缀集合__A: "A", "BA", "ABA", "BABA"公共前后缀: "A" 和 "ABA"
最长公共前后缀: "ABA" (长度=3)
NEXT数组计算过程
其实就是遍历模式串,如果发现两个重复的子串,则记录两个子串重复的长度,便于回溯时,不匹配时回溯到第一个子串后面。
所以next[j]表示:当模式串在第j个字符匹配失败时,应该跳转到哪个位置继续比较。
图解

流程图如下:
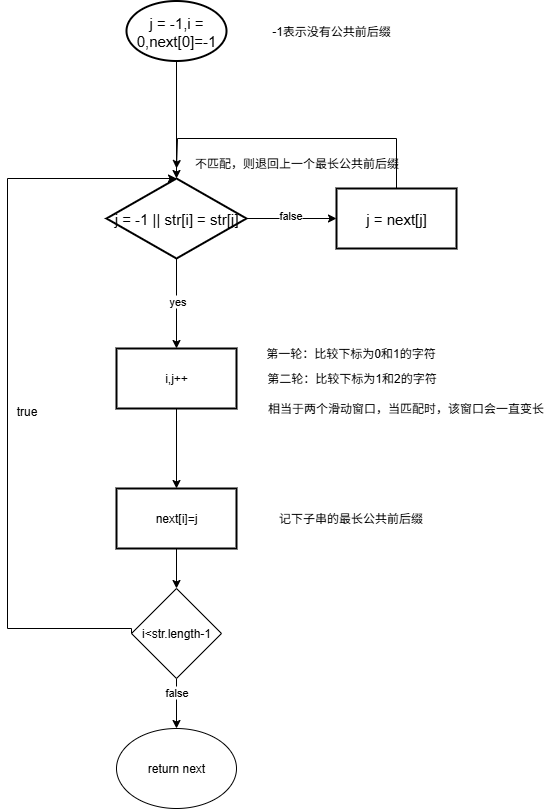
代码
public class KMPAlgorithm {/*** 计算next数组* next[i]表示模式串中[0, i-1]子串的最长相等前后缀长度*/private static int[] computeNext(String pattern) {int m = pattern.length();int[] next = new int[m];next[0] = -1; // 第一个字符没有前缀,设为-1int i = 0; // 模式串指针int j = -1; // 最长相等前后缀长度while (i < m - 1) {if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {// 字符匹配成功,前后缀长度都增加i++;j++;next[i] = j;} else {// 字符不匹配,回溯到前一个最长相等前后缀位置j = next[j];}}return next;}/*** 优化的next数组计算(处理连续相同字符的情况)*/private static int[] computeNextOptimized(String pattern) {int m = pattern.length();int[] next = new int[m];next[0] = -1;int i = 0;int j = -1;while (i < m - 1) {if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {i++;j++;// 优化:如果跳转后的字符相同,则继续跳转if (pattern.charAt(i) != pattern.charAt(j)) {next[i] = j;} else {next[i] = next[j];}} else {j = next[j];}}return next;}
}
KMP匹配计算过程
用两个指针分别指向主串和模式串,如果不匹配,则根据next数组,回归模式串指针。
通过next数据来避免每次匹配失败都回滚指针到0,且主串指针不用回滚。
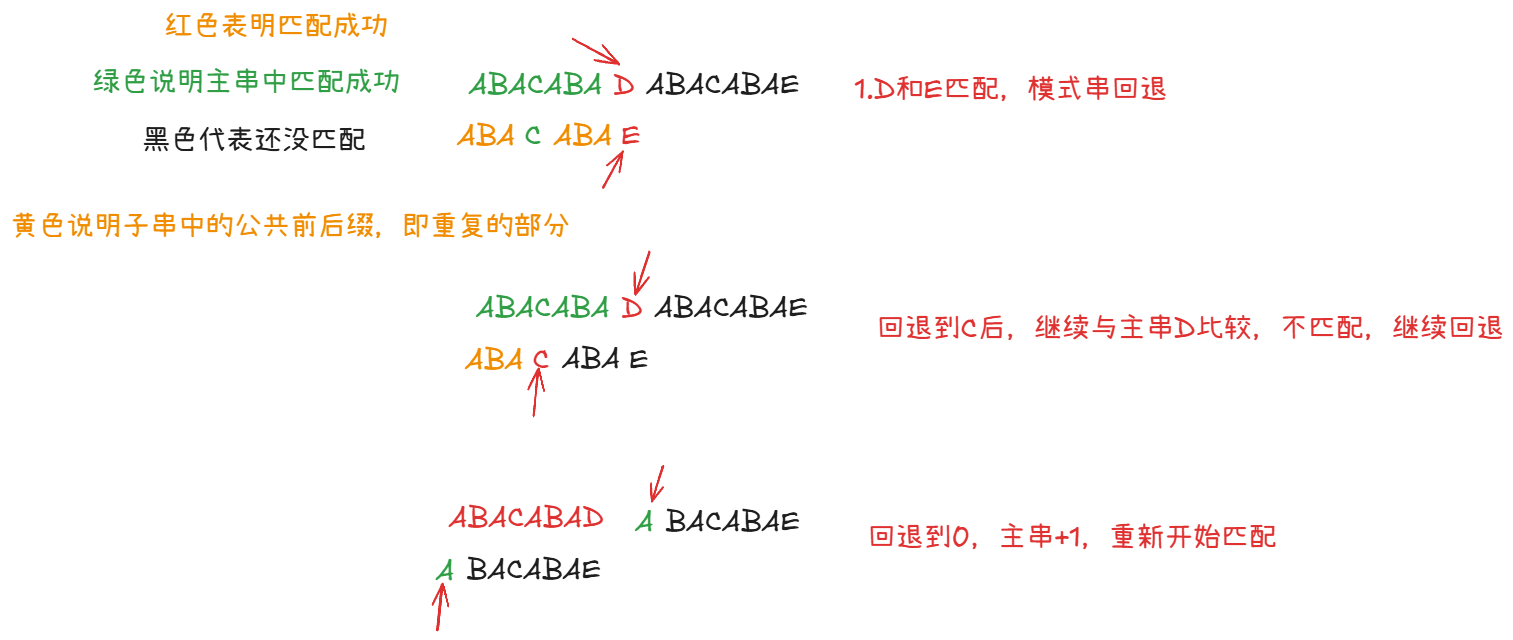
代码
public class KMPAlgorithm {/*** KMP字符串匹配算法* @param text 主文本串* @param pattern 模式串* @return 匹配的起始位置,未找到返回-1*/public static int kmpSearch(String text, String pattern) {if (text == null || pattern == null) {return -1;}int n = text.length();int m = pattern.length();if (m == 0) return 0; // 空模式串匹配任何文本的开始if (n < m) return -1; // 文本比模式串短// 计算next数组int[] next = computeNextOptimized(pattern);int i = 0; // 文本串指针int j = 0; // 模式串指针while (i < n && j < m) {if (j == -1 || text.charAt(i) == pattern.charAt(j)) {// 字符匹配成功,两个指针都前进i++;j++;} else {// 字符匹配失败,模式串指针根据next数组跳转// 文本串指针i不回溯!j = next[j];}}// 判断是否找到完整匹配if (j == m) {return i - j; // 返回匹配的起始位置} else {return -1; // 未找到匹配}}/*** 测试用例*/public static void main(String[] args) {String text = "ABABDABACDABABCABAB";String pattern = "ABABCABAB";int position = kmpSearch(text, pattern);if (position != -1) {System.out.println("模式串在主文本串中的位置: " + position);System.out.println("匹配内容: " + text.substring(position, position + pattern.length()));} else {System.out.println("未找到匹配");}// 性能对比测试testPerformance();}/*** 性能测试:KMP vs 暴力匹配*/private static void testPerformance() {// 构造一个较长的文本串和模式串StringBuilder textBuilder = new StringBuilder();for (int i = 0; i < 100000; i++) {textBuilder.append("ABC");}textBuilder.append("TARGET_PATTERN");for (int i = 0; i < 100000; i++) {textBuilder.append("XYZ");}String text = textBuilder.toString();String pattern = "TARGET_PATTERN";// KMP算法测试long startTime = System.nanoTime();int kmpResult = kmpSearch(text, pattern);long kmpTime = System.nanoTime() - startTime;// 暴力匹配测试startTime = System.nanoTime();int bfResult = BruteForce.bruteForceSearch(text, pattern);long bfTime = System.nanoTime() - startTime;System.out.println("\n性能对比:");System.out.println("KMP算法: " + kmpTime + " 纳秒, 位置: " + kmpResult);System.out.println("暴力匹配: " + bfTime + " 纳秒, 位置: " + bfResult);System.out.println("KMP比暴力匹配快 " + (bfTime * 1.0 / kmpTime) + " 倍");}
}
与暴力破解的对比
| 算法 | 时间复杂度 | 空间复杂度 | 特点 |
|---|---|---|---|
| 暴力匹配 | O(n×m) | O(1) | 实现简单,效率低 |
| KMP算法 | O(n+m) | O(m) | 预处理next数组,匹配高效 |
暴力破解代码(滑动窗口)
public class BruteForce {public static int bruteForceSearch(String text, String pattern) {int n = text.length();int m = pattern.length();for (int i = 0; i <= n - m; i++) {int j;for (j = 0; j < m; j++) {if (text.charAt(i + j) != pattern.charAt(j)) {break; // 发现不匹配,立即跳出}}if (j == m) {return i; // 找到匹配}}return -1; // 未找到匹配}
}
