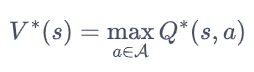强化学习基础——各字母含义与马尔可夫决策

        马尔可夫性简单来说就是 当且仅当某时刻的状态只取决于上一时刻的状态时，而与再往之前时刻与之后时刻无关。(具体感兴趣可百度)

马尔可夫奖励过程（MRP）

        接下来基于上述符号引入几个概念：

回报 ：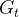

其中，表示在时刻获得的奖励，权重因子表示未来时刻奖励具有不确定性，因此需要有权重衰减。

价值函数 V(s)：

其中 E 代表均值。

        上式就是马尔可夫奖励过程中非常有名的贝尔曼方程（Bellman equation），对每一个状态都成立。

马尔可夫决策过程（MDP）

        在马尔可夫奖励过程（MRP）的基础上加入动作，就得到了马尔可夫决策过程（MDP）。

马尔可夫决策过程由元组  构成，其中：

         MDP 与 MRP 非常相像，主要区别为 MDP 中的状态转移函数和奖励函数都比 MRP 多了动作 a 作为自变量。各部分关系如下图所示：

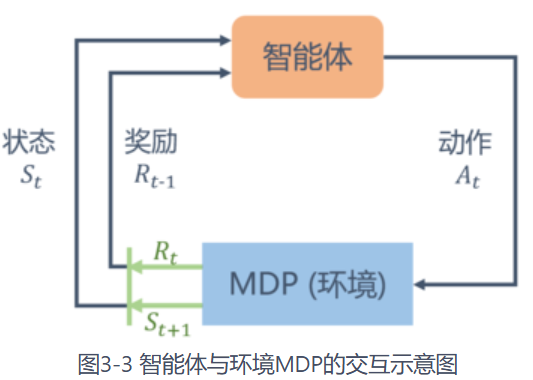
        接下来就马尔可夫决策过程引入几个概念：
策略 ：
策略  是一个函数，表示在输入状态情况下采取动作的概率。当一个策略是确定性策略（deterministic policy）时，它在每个状态时只输出一个确定性的动作，即只有该动作的概率为 1，其他动作的概率为 0；当一个策略是随机性策略（stochastic policy）时，它在每个状态时输出的是关于动作的概率分布，然后根据该分布进行采样就可以得到一个动作。在 MDP 中，由于马尔可夫性质的存在，策略只需要与当前状态有关，不需要考虑历史状态。

状态价值函数 

动作价值函数 

贝尔曼期望方程

贝尔曼最优方程

        最优策略都有相同的状态价值函数，我们称之为最优状态价值函数，表示为：

        同理，我们定义最优动作价值函数:

        这与在普通策略下的状态价值函数和动作价值函数之间的关系是一样的。另一方面，最优状态价值是选择此时使最优动作价值最大的那一个动作时的状态价值：