oj 素数个数 难

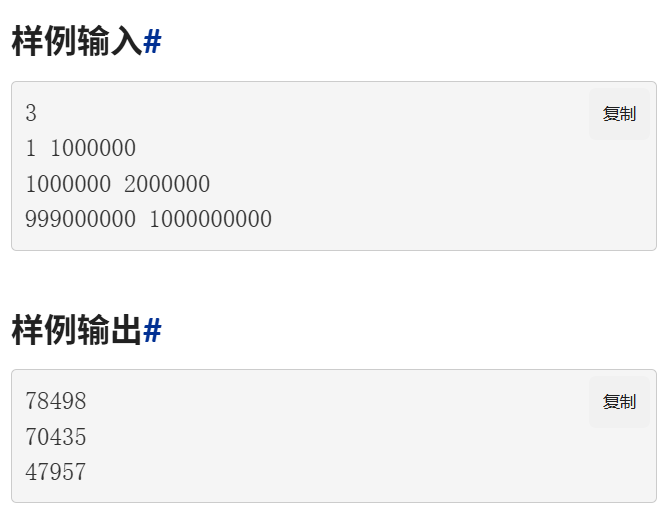
思路：先设立一个2~sqrt(r)小素数数组，只要用<=sqrt(r)的素数，就可以筛掉[L,R]中所有的合数(因为一个合数的最小质因数一定小于等于它的平方根)，标记这个小素数组可以用埃筛；第二部就是对[L,R]中的合数进行筛出，可以见代码

// 初始化区间 [L, R] 的标记数组（使用静态数组）int is_prime[MAX_RANGE];for (int i = 0; i <= R - L; i++) {is_prime[i] = 1;//默认全为质数}// 用每个小素数 p 筛除区间内的合数for (int i = 0; i < small_primes_count; i++) {int p = small_primes[i];// 找到区间内第一个 >= L 且能被 p 整除的数int start = fmax(p * p, (( (L/p) + 1) * p));//对l/p向上取整再乘p，保证start再[L,R]内for (int multiple = start; multiple <= R; multiple += p) {is_prime[multiple - L] = 0;//一个个找它们倍数}}

这个思路的好处就是，即使R最大可能为1e9，但也只需要小质数数组里面最大求出不到1e5范围内的质数，然后一个个找他们的倍数

---

AC代码：

#include <stdio.h>
#include <math.h>#define MAX_RANGE 1000001  // 因为 R - L <= 10^6，所以最大需要 10^6 + 1 大小的数组// 计算区间 [L, R] 内的素数个数
int countPrimes(int L, int R) {// 处理 L=1 的特殊情况，1 不是素数if (L == 1) {L = 2;}// 计算 sqrt(R)，确定小素数的范围int sqrt_R = (int)sqrt(R);// 筛出所有 <= sqrt(R) 的素数（使用静态数组）int small_primes[MAX_RANGE];  // 足够大的数组存储小素数int small_primes_count = 0;int is_small_prime[MAX_RANGE];  // 标记是否为小素数for (int i = 0; i <= sqrt_R; i++) {is_small_prime[i] = 1;}is_small_prime[0] = is_small_prime[1] = 0;for (int i = 2; i <= sqrt_R; i++) {if (is_small_prime[i]) {small_primes[small_primes_count++] = i;for (int j = i * i; j <= sqrt_R; j += i) {is_small_prime[j] = 0;}}}// 初始化区间 [L, R] 的标记数组（使用静态数组）int is_prime[MAX_RANGE];for (int i = 0; i <= R - L; i++) {is_prime[i] = 1;}// 用每个小素数 p 筛除区间内的合数for (int i = 0; i < small_primes_count; i++) {int p = small_primes[i];// 找到区间内第一个 >= L 且能被 p 整除的数int start = fmax(p * p, (( (L+p-1)/p) * p));for (int multiple = start; multiple <= R; multiple += p) {is_prime[multiple - L] = 0;}}// 统计素数个数int count = 0;for (int i = 0; i <= R - L; i++) {if (is_prime[i]) {count++;}}return count;
}int main() {int T;scanf("%d", &T);while (T--) {int L, R;scanf("%d %d", &L, &R);printf("%d\n", countPrimes(L, R));}return 0;
}