复变函数与积分变换 第一章——复数与复变函数

一、复数及复变函数的概念与复数代数运算

1、复数及复变函数的概念

（1）复数是一种数学概念，可表示为。

①x被称为复数的实部，它是复数的实数部分，可记为。

②y被称为复数的虚部，它是复数中伴随虚数单位i的系数（同样为实数），可记为。

③虚数单位i与实数的关系为。

④有时虚数单位也用j表示。

（2）复变函数是自变量为复数的函数。

2、复数及其代数运算

（1）关于复数的几个概念：

（2）任意两个复数之间不能比较大小（或者说不能直接比较大小），不过如果两个复数的实部和虚部均相等，则可认为两个复数相等，反之同样成立。

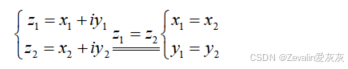
（3）复数的代数运算：

①加法与减法：两个复数的实部与虚部分别相加即可。

②乘法：按照多项式乘法法则计算即可。

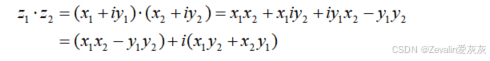
③除法：根据平方差公式将分母有理化，然后按照多项式乘法法则计算即可。

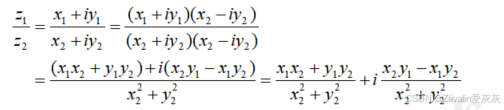
（4）共轭复数的性质：

①代数运算的性质：

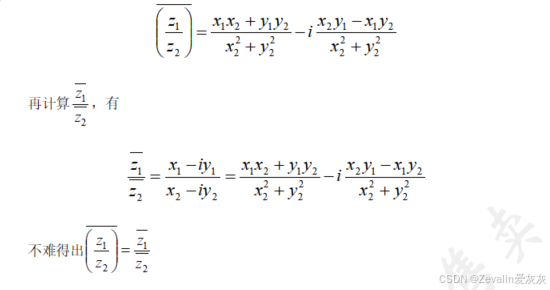
②对一个复数连续取两次共轭，结果为它本身，即，证明如下：

③一个复数与其共轭复数相乘，结果为复数的模平方，证明如下：

④一个复数与其共轭复数相加，结果实部为原本的两倍，虚部为0，而一个复数与其共轭复数相减，结果实部为0，虚部为原本的两倍，证明如下：

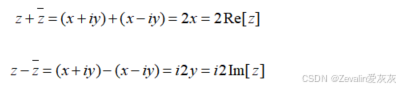
3、例题

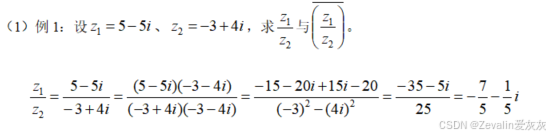
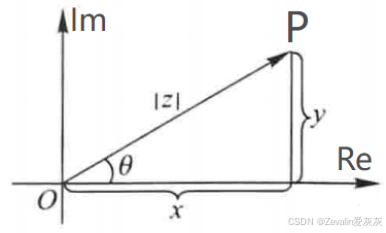
二、复数的几何意义

1、复数的其它表示方法

（1）复数可借助复平面表示，复平面的横轴为复数的实部（实轴），纵轴为复数的虚部（虚轴），如下图所示。