Numpy学习总结

目录

一、认识 NumPy：什么是 NumPy？

二、为什么 NumPy 这么快？

三、准备工作：安装与导入

1. 安装 NumPy

2. 导入 NumPy

四、核心概念：什么是 “数组（ndarray）”？

五、数组基础：创建、访问与修改

1. 从 Python 列表创建数组

2. 访问数组元素

3. 修改数组元素

六、数组属性：快速了解数组 “长相”

七、常用数组创建方法

八、数组操作：排序、连接与重塑

1. 排序

2. 连接数组

3. 重塑数组

九、索引与切片：精准提取数据

1. 1 维数组切片

2. 2 维数组切片

十、数组数学计算：告别循环

1. 基本运算（加减乘除）

2. 广播（Broadcasting）

十一、统计与聚合：快速分析数据

十二、矩阵操作：转置与运算

1. 矩阵转置

2. 矩阵加法

十三、实战：用 NumPy 实现数学公式

总结

在 Python 科学计算领域，NumPy 绝对是 “基石” 般的存在。无论是数据分析、机器学习还是信号处理，几乎都离不开它的身影。

一、认识 NumPy：什么是 NumPy？

NumPy 全称为 Numerical Python，是 Python 中用于科学计算的基础库。它最核心的能力是提供了多维数组对象（ndarray），以及一套针对数组的高效操作工具，涵盖：

• 数学运算（加减乘除、矩阵运算等）

• 逻辑判断与筛选

• 数组形状调整（重塑、转置）

• 排序、统计分析（均值、标准差等）

• 随机模拟与傅里叶变换

简单说：有了 NumPy，你才能在 Python 里高效处理 “批量数据”，而不是用列表写一堆循环。

二、为什么 NumPy 这么快？

用过 NumPy 的人都会觉得它 “快得离谱”，核心原因是 向量化（Vectorization）。

向量化的本质是：用预编译的 C 代码替代 Python 中的显式循环。比如计算两个列表对应元素相加，Python 列表需要写 for 循环，而 NumPy 数组直接用 + 就能搞定 —— 背后的循环在 C 层面执行，速度提升几十倍。

向量化还有 3 个优点：

1. 代码更简洁：一行代码替代循环，可读性更高

1. bug 更少：行数少了，出错的概率自然降低

1. 贴近数学符号：比如矩阵乘法、向量运算，写法和数学公式几乎一致

三、准备工作：安装与导入

1. 安装 NumPy

推荐指定版本（避免版本兼容问题），用 pip 直接安装：

# 安装 1.19.2 版本（稳定常用）!pip install numpy==1.19.2

2. 导入 NumPy

惯例是导入后简写为 np（行业通用，不用纠结）：

import numpy as np

四、核心概念：什么是 “数组（ndarray）”？

数组是 NumPy 的 “灵魂”，全称 N-dimensional array（N 维数组）。我们可以这样理解不同维度的数组：

• 1 维数组：像一个普通列表，比如 [1,2,3,4]

• 2 维数组：像一个表格，有行有列，比如 Excel 表格

• 3 维数组：像一叠表格，比如多页 Excel 工作表叠在一起

在 NumPy 中，所有数组都属于 ndarray 类型，后续操作都是围绕它展开。

五、数组基础：创建、访问与修改

1. 从 Python 列表创建数组

最常用的方式是把 Python 列表传入 np.array()：

# 1 维数组a_list = [1, 2, 3, 4, 5]arr1 = np.array(a_list)print("1 维数组：", arr1) # 输出：[1 2 3 4 5]# 2 维数组（嵌套列表）b_list = [[1, 2, 3], [4, 5, 6]]arr2 = np.array(b_list)print("2 维数组：\n", arr2) # 输出：[[1 2 3],[4 5 6]]

2. 访问数组元素

和 Python 列表类似，用 索引（从 0 开始） 访问，2 维数组需要指定 “行索引 + 列索引”：

# 访问 1 维数组第 1 个元素（索引 0）print(arr1[0]) # 输出：1# 访问 2 维数组第 2 行第 3 列（索引 1,2）print(arr2[1, 2]) # 输出：6

3. 修改数组元素

直接通过索引赋值即可（数组是 “可变” 的）：

arr1[0] = 10 # 把第 1 个元素改成 10print(arr1) # 输出：[10 2 3 4 5]

六、数组属性：快速了解数组 “长相”

每个 ndarray 都有 4 个核心属性，帮你快速掌握数组的基本信息：

# 以 2 维数组 arr2 为例print("数组维度（ndim）：", arr2.ndim) # 输出：2（2 维数组）print("数组形状（shape）：", arr2.shape) # 输出：(2, 3)（2 行 3 列）print("总元素数（size）：", arr2.size) # 输出：6（2*3=6 个元素）print("数据类型（dtype）：", arr2.dtype) # 输出：int64（默认整数类型）

七、常用数组创建方法

除了从列表转换，NumPy 还提供了多种便捷的数组创建函数，覆盖日常需求：

函数	功能说明	代码示例	输出结果
np.zeros(shape)	创建全 0 数组	np.zeros((2,2))	[[0. 0.],[0. 0.]]
np.ones(shape)	创建全 1 数组	np.ones((2,2))	[[1. 1.],[1. 1.]]
np.empty(shape)	创建空数组（值为内存随机值，速度快）	np.empty(3)	[1. 2. 3.]（示例值）
np.arange(start, end, step)	按步长创建数组（类似 range）	np.arange(0,10,2)	[0 2 4 6 8]
np.linspace(start, end, num)	按个数创建均匀间隔数组	np.linspace(0,10,5)	[ 0. 2.5 5. 7.5 10. ]

代码演示：

# 全 0 数组（2 行 2 列）zeros_arr = np.zeros((2, 2))print("全 0 数组：\n", zeros_arr)# 均匀间隔数组（0 到 10，共 5 个元素）lin_arr = np.linspace(0, 10, 5)print("均匀间隔数组：", lin_arr)

八、数组操作：排序、连接与重塑

1. 排序

用 np.sort() 实现，默认升序；降序只需加 [::-1]（倒序切片）：

arr = np.array([3, 2, 6, 9, 10, 8])# 升序asc_arr = np.sort(arr)print("升序：", asc_arr) # 输出：[ 2 3 6 8 9 10]# 降序desc_arr = np.sort(arr)[::-1]print("降序：", desc_arr) # 输出：[10 9 8 6 3 2]

2. 连接数组

用 np.concatenate((arr1, arr2)) 连接多个数组（需保证维度兼容）：

a = np.array([1, 2, 3])b = np.array([4, 5, 6])# 连接两个 1 维数组concat_arr = np.concatenate((a, b))print("连接后：", concat_arr) # 输出：[1 2 3 4 5 6]

3. 重塑数组

用 reshape(shape) 改变数组形状，前提是总元素数不变（比如 6 个元素可重塑为 2x3 或 3x2）：

arr = np.array([3, 2, 6, 9, 10, 8]) # 共 6 个元素# 重塑为 2 行 3 列reshape_arr = arr.reshape((2, 3))print("重塑后（2x3）：\n", reshape_arr)

九、索引与切片：精准提取数据

NumPy 数组的索引和切片和 Python 列表几乎一致，但支持 “多维切片”，非常灵活：

1. 1 维数组切片

data = np.array([1, 2, 3, 4, 5])print("索引 1 的元素：", data[1]) # 输出：2（第 2 个元素）print("0-2（不含 2）的元素：", data[0:2]) # 输出：[1 2]print("1 之后的所有元素：", data[1:]) # 输出：[2 3 4 5]print("倒数 2 个元素：", data[-2:]) # 输出：[4 5]

2. 2 维数组切片

格式：arr[行切片, 列切片]

data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 第 2-3 行（索引 1-2），第 1 列（索引 0）slice_arr = data[1:3, 0]print("切片结果：", slice_arr) # 输出：[4 7]

十、数组数学计算：告别循环

NumPy 数组支持 “element-wise”（元素级）运算，无需写循环，直接用算术运算符即可。

1. 基本运算（加减乘除）

# 定义两个数组data = np.array([1, 2, 3])ones = np.ones(3, dtype=int) # 全 1 数组（整数类型）# 加法print("加法：", data + ones) # 输出：[2 3 4]# 减法print("减法：", data - ones) # 输出：[0 1 2]# 乘法（元素级）print("乘法：", data * data) # 输出：[1 4 9]# 除法（元素级）print("除法：", data / data) # 输出：[1. 1. 1.]

2. 广播（Broadcasting）

当数组和标量（单个数字） 运算时，NumPy 会自动把标量 “广播” 到数组的每个元素，非常实用：

# 场景：将英里转换为公里（1 英里 = 1.6 公里）miles = np.array([1.0, 2.0, 3.0])km = miles * 1.6 # 标量 1.6 广播到每个元素print("公里数：", km) # 输出：[1.6 3.2 4.8]

⚠️ 注意：广播只支持 “维度兼容” 的情况（比如 2x3 数组和 1x3 数组可广播，和 1x2 数组不行），否则会报错。

十一、统计与聚合：快速分析数据

NumPy 提供了常用的统计函数，支持对整个数组或指定 “轴”（行 / 列）计算：

函数	功能	代码示例（arr 为 2 维数组）
max()	最大值	arr.max()（全局）/ arr.max(axis=0)（列最大值）
min()	最小值	arr.min() / arr.min(axis=1)（行最小值）
sum()	求和	arr.sum() / arr.sum(axis=0)
mean()	平均值	arr.mean()
std()	标准差	arr.std()
prod()	所有元素乘积	arr.prod()

代码演示：

# 2 维数组a = np.array([[0.45, 0.17, 0.34],[0.55, 0.05, 0.40],[0.13, 0.82, 0.27]])# 全局最大值print("全局最大值：", a.max()) # 输出：0.82# 每列最小值（axis=0 代表列）print("每列最小值：", a.min(axis=0)) # 输出：[0.13 0.05 0.27]# 每行平均值（axis=1 代表行）print("每行平均值：", a.mean(axis=1)) # 输出：[0.32 0.333 0.407]

十二、矩阵操作：转置与运算

在 NumPy 中，2 维数组就是矩阵，支持矩阵特有的操作：

1. 矩阵转置

用 T 属性或 transpose() 方法，实现 “行变列、列变行”：

data = np.array([[1, 2, 3], [4, 5, 6]]) # 2 行 3 列# 转置（变成 3 行 2 列）trans_data = data.Tprint("转置后：\n", trans_data)

2. 矩阵加法

和数组加法一致，需保证两个矩阵 “形状相同”：

data = np.array([[1, 2], [3, 4]])ones_mat = np.ones((2, 2), dtype=int) # 2x2 全 1 矩阵print("矩阵加法：\n", data + ones_mat)# 输出：# [[2 3]# [4 5]]

十三、实战：用 NumPy 实现数学公式

NumPy 的一大优势是 “贴近数学公式”，比如机器学习中常用的 均方误差（MSE） 公式：

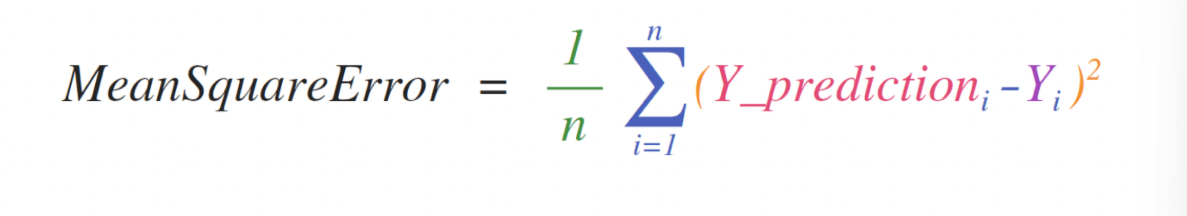
在 NumPy 中实现此公式简单明了

之所以如此有效，是因为 predictions 和 labels 可以包含一个或一千个值。它们只需要大小相同。

您可以这样可视化它

在此示例中，预测向量和标签向量都包含三个值，这意味着 n 的值为三。执行减法后，向量中的值被平方。然后 NumPy 对这些值求和，结果是该预测的误差值和模型质量评分。

用 NumPy 实现只需 1 行代码：

# 模拟数据（3 个样本）labels = np.array([2, 3, 4])  真实标签predictions = np.array([1.5, 3.2, 3.8])  预测值# 计算均方误差mse = np.mean((labels - predictions) ** 2)print("均方误差：", mse) # 输出：0.0867（近似值）

总结

NumPy 是 Python 科学计算的 “基石”，核心是 ndarray 数组和向量化操作。覆盖了从 “安装导入” 到 “实战公式” 的全流程，包括：

• 数组创建与属性

• 索引、切片与重塑

• 数学运算与广播

• 统计聚合与矩阵操作

想要熟练掌握 NumPy，最好的方式是 “边看边练”—— 把文中的代码跑一遍，修改参数试试效果，很快就能上手！