【深度强化学习】#6 TRPOPPO：策略优化算法

以Actor-Critic为起点，DDPG和TD3继承DQN的思想，以确定性策略为核心，不断优化价值函数学习的稳定性和准确度。与此同时，还有一条技术路线仍然坚持随机性策略，围绕策略函数训练过程的安全与稳健展开研究，由此诞生了TRPO和PPO两大策略优化算法。

TRPO

在Actor-Critic中，我们会面临策略梯度更新步长的设置问题，即对于策略更新公式

$${\theta }_{t+1}={\theta }_t+{\alpha }_{\theta }{\nabla }_{\theta }\ln {\pi }_{\theta }(a_t|s_t)\cdot V_w(s_t,a_t)$$

如果步长${\alpha }_{\theta }$太小，则策略的学习速度极慢，需要大量样本，训练成本高；如果步长${\alpha }_{\theta }$太大，则会导致策略更新剧烈变化，可能会带来灾难性的性能下降，一次将策略打回原形的错误更新会浪费之前的所有样本。

TRPO（Trust Region Policy Optimization，信任区域策略优化）致力于避免步长设置过大，其核心思想是确保每次更新，新策略不会和旧策略差异过大，即将新策略限制在旧策略的一个“信任区域”内。

优化目标

策略是一种概率分布，衡量两种概率分布的差异的一个指标是KL散度。如果一个随机变量$\mathrm{x}$有两个单独的概率分布$p(x)$和$q(x)$，则它们以$p(x)$为基准分布的KL散度为

$$\begin{array}{rl}{D}_{\mathrm{KL}}(p||q)& ={\mathbb{E}}_{\mathrm{x}\sim p}\left[\log \frac{p(x)}{q(x)}\right]\end{array}$$

概率分布差异越大，KL散度越大。TRPO的优化目标即在优化策略的同时对新旧策略的KL散度进行约束。TRPO的目标函数为

$$J(\theta )={\mathbb{E}}_{(s,a)\sim {\pi }_{\mathrm{old}}}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{\mathrm{old}}(a|s)}{A}_{{\pi }_{\mathrm{old}}}(s,a)\right]$$

最大化该目标函数的意义是找到一个新的参数$\theta$，使得在新策略下，那些优势高的动作被更大比例地采用。

约束条件为

$${\mathbb{E}}_{s\sim {\pi }_{\mathrm{old}}}[D_{\mathrm{KL}}({\pi }_{\mathrm{old}}(\cdot |s)||{\pi }_{\theta }(\cdot |s))]\le \delta$$

其中$\delta$为KL散度的约束阈值，即信任区域的阈值，防止策略更新过渡。

解决这一优化问题需要泰勒展开、拉格朗日乘子法和共轭梯度法三步骤。

（优化问题的求解过程选择性阅读）

泰勒展开

泰勒展开可以让我们从梯度视角更清晰地把握优化问题。对于目标函数$J(\theta )$，假设当前策略参数为${\theta }_{\mathrm{old}}$，新策略参数为${\theta }_{\mathrm{new}}={\theta }_{\mathrm{old}}+\Delta \theta$，则目标函数可以在${\theta }_{\mathrm{old}}$附近展开为

$$J({\theta }_{\mathrm{new}})\approx J({\theta }_{\mathrm{old}})+g^T\Delta \theta$$

其中$g={\nabla }_{\theta }J({\theta }_{\mathrm{old}})$是目标函数在${\theta }_{\mathrm{old}}$的梯度，表示当前策略方向上的上升斜率。

对期望KL散度的泰勒展开过程则比较复杂。我们先针对单个KL散度，简记当前策略为$p(\theta )$，新策略为$p(\theta +\Delta \theta )$，将KL散度视为$\Delta \theta$的函数

$$D_{\mathrm{KL}}(p(\theta )||p(\theta +\Delta \theta ))={\mathbb{E}}_{x\sim p(\theta )}\left[\log \frac{p(x|\theta )}{p(x|\theta +\Delta \theta )}\right]$$

接下来在$\Delta \theta =0$处对其进行泰勒展开。对于零阶项，即KL散度本身，此时两个分布完全相同，值为零

$$D_{\mathrm{KL}}(\theta ||\theta )=0$$

一阶项是KL散度在$\Delta \theta =0$处的梯度

$$\begin{array}{rl}g& ={\nabla }_{\Delta \theta }{D}_{\mathrm{KL}}(p(\theta )||p(\theta +\Delta \theta )){|}_{\Delta \theta =0}\\ & ={\nabla }_{\Delta \theta }{\mathbb{E}}_{x\sim p(\theta )}\left[\log \frac{p(x|\theta )}{p(x|\theta +\Delta \theta )}\right]{|}_{\Delta \theta =0}\\ & =-{\mathbb{E}}_{x\sim p(\theta )}[{\nabla }_{\Delta \theta }\log p(x|\theta +\Delta \theta )]{|}_{\Delta \theta =0}\\ \text{（引入中间变量}\varphi =\theta +\Delta \theta \text{）}& =-{\mathbb{E}}_{x\sim p(\theta )}\left[\frac{\partial \varphi }{\partial \Delta \theta }{\nabla }_{\varphi }\log p(x|\varphi )\right]{|}_{\Delta \theta =0}\\ & =-{\mathbb{E}}_{x\sim p(\theta )}[{\nabla }_{\varphi }\log p(x|\varphi )]{|}_{\Delta \theta =0}\\ & =-{\mathbb{E}}_{x\sim p(\theta )}[{\nabla }_{\theta }\log p(x|\theta )]\end{array}$$

其中${\nabla }_{\theta }\log p(x|\theta )$被称为得分函数，它的一个重要性质即期望为零

$$\begin{array}{rl}{\mathbb{E}}_{a\sim {\pi }_{\theta }}[{\nabla }_{\theta }\log p(x|\theta )]& =\int p(x|\theta )\cdot {\nabla }_{\theta }\log p(x|\theta )\mathrm{d}x\\ \text{（自然对数导数性质）}& =\int p(x|\theta )\cdot \frac{{\nabla }_{\theta }p(x|\theta )}{p(x|\theta )}\mathrm{d}x\\ & =\int {\nabla }_{\theta }p(x|\theta )\mathrm{d}x\\ \text{（梯度变量与积分变量不一致时，梯度算符可提出）}& ={\nabla }_{\theta }\int p(x|\theta )\mathrm{d}x\\ \text{（概率分布的归一化条件）}& ={\nabla }_{\theta }1=0\end{array}$$

因此一阶项也为零。

对于二阶项（黑塞矩阵$H$），目前有

$$\begin{array}{rl}H& ={\nabla }_{\Delta \theta }g\\ & =-{\mathbb{E}}_{x\sim p(\theta )}[{\nabla }_{\theta }^2\log p(x|\theta )]\end{array}$$

我们先简记得分函数${\nabla }_{\theta }\log p(x|\theta )=s(x,\theta )$，则${\nabla }_{\theta }^2\log p(x|\theta )={\nabla }_{\theta }s(x,\theta )$。现在从概率分布的归一化条件开始

$$\begin{array}{cc}& \int p(x|\theta )\mathrm{d}x=1\\ \text{（两边对}\theta \text{求梯度）}& {\nabla }_{\theta }\int p(x|\theta )\mathrm{d}x=0\\ & \int {\nabla }_{\theta }p(x|\theta )\mathrm{d}x=0\\ \text{（对数求导法则）}& \int p(x|\theta ){\nabla }_{\theta }\log p(x|\theta )\mathrm{d}x=0\\ & \int p(x|\theta )s(x,\theta )\mathrm{d}x=0\\ \text{（两边对}\theta \text{再次求梯度）}& {\nabla }_{\theta }\int p(x|\theta )s(x,\theta )\mathrm{d}x=0\\ & \int {\nabla }_{\theta }[p(x|\theta )s(x,\theta )]\mathrm{d}x=0\\ \text{（乘积求导法则）}& \int [({\nabla }_{\theta }p(x|\theta ))s(x,\theta {)}^T+p(x|\theta ){\nabla }_{\theta }s(x,\theta )]\mathrm{d}x=0\\ \text{（再次对数求导法则）}& \int [p(x|\theta )s(x,\theta )s(x,\theta {)}^T+p(x|\theta ){\nabla }_{\theta }s(x,\theta )]\mathrm{d}x=0\\ & \int p(x|\theta )s(x,\theta )s(x,\theta {)}^T\mathrm{d}x+\int p(x|\theta ){\nabla }_{\theta }s(x,\theta )\mathrm{d}x=0\\ \text{（期望表示）}& {\mathbb{E}}_{x\sim p(\theta )}[s(x,\theta )s(x,\theta {)}^T]+{\mathbb{E}}_{x\sim p(\theta )}[{\nabla }_{\theta }s(x,\theta )]=0\end{array}$$

于是黑塞矩阵

$$\begin{array}{rl}H& ={\mathbb{E}}_{x\sim p(\theta )}[{\nabla }_{\theta }s(x,\theta )]\\ & =-{\mathbb{E}}_{x\sim p(\theta )}[s(x,\theta )s(x,\theta {)}^T]\\ & =-{\mathbb{E}}_{x\sim p(\theta )}[({\nabla }_{\theta }\log p(x|\theta ))({\nabla }_{\theta }\log p(x|\theta ){)}^T]\end{array}$$

结果为负的得分函数外积的期望，即费雪信息矩阵，在统计学中用于度量随机变量样本所能提供的关于多维参数的信息量

$$F=-{\mathbb{E}}_{x\sim p(\theta )}[({\nabla }_{\theta }\log p(x|\theta ))({\nabla }_{\theta }\log p(x|\theta ){)}^T]$$

最终，期望KL散度的泰勒展开仅包含二阶项

$$\begin{array}{rl}& {\mathbb{E}}_{s\sim {\pi }_{\mathrm{old}}}[D_{\mathrm{KL}}({\pi }_{\mathrm{old}}(\cdot |s)||{\pi }_{\theta }(\cdot |s))]\\ \approx & {\mathbb{E}}_{s\sim {\pi }_{\mathrm{old}}}\left[\frac{1}{2}\Delta {\theta }^T{F}_s({\theta }_{\mathrm{old}})\Delta \theta \right]\\ =& \frac{1}{2}\Delta {\theta }^T{E}_{s\sim {\pi }_{\mathrm{old}}}[F_s({\theta }_{\mathrm{old}})]\Delta \theta \\ =& \frac{1}{2}\Delta {\theta }^T\bar{F}({\theta }_{\mathrm{old}})\Delta \theta \end{array}$$

现在，优化问题变为了在KL散度约束的情况下，找到一个参数更新方向$\Delta \theta$使得目标函数变化量最大

$$\underset{\Delta \theta }{\max }{g}^T\Delta \theta ,\text{ s.t.}\frac{1}{2}\Delta {\theta }^T\bar{F}\Delta \theta \le \delta$$

拉格朗日乘数法

对于该线性目标函数和二次凸集约束，要达到最优解的约束必然是紧的，即约束条件取边界

$$\frac{1}{2}\Delta {\theta }^T\bar{F}\Delta \theta =\delta$$

考虑最简单的二维情况，此时线性函数是一个平面，二次型凸集是以当前点为中心的一个椭球。对于一个平面上的点，除了梯度$g^T=0$的情况，椭球范围内的最大值必然落在边界。

现在我们可以使用拉格朗日乘数法在$\frac{1}{2}\Delta {\theta }^T\bar{F}\Delta \theta -\delta =0$的条件下对$g^T\Delta \theta$求极值。构造拉格朗日函数

$$\mathcal{L}(\Delta \theta ,\lambda )=g^T\Delta \theta -\lambda (\frac{1}{2}\Delta {\theta }^T\bar{F}\Delta \theta -\delta )$$

令其对$\Delta \theta$的导数为零，得到

$${\nabla }_{\Delta \theta }\mathcal{L}=g-\lambda \bar{F}\Delta \theta =0$$

解得

$$\Delta \theta =\frac{1}{\lambda }{\bar{F}}^{-1}g$$

共轭梯度法

在巨大的参数量下，对$\bar{F}$求逆矩阵在计算和存储上都是难以实现的，我们只能通过迭代法求解。令$\Delta \theta =x$，且不考虑标量$\lambda$，则要求解的线性方程组为

$$\bar{F}x=g$$

TRPO使用了共轭梯度法。共轭梯度法作为最优化理论的知识，不是TRPO的核心内容，本文仅作通俗介绍。

在此之前，我们先了解更基础的迭代优化算法：最速下降法。它是深度学习中常规梯度下降的理论基础，其核心思想即沿着当前点梯度方向的反方向进行更新以最小化损失函数。不同之处在于，更新的步长在梯度下降中由学习率控制，而在最速下降法中是通过沿着更新方向搜索函数的最小值确定的。

最速下降法的缺点在于迭代过程存在振荡，考虑一个等值线如下的椭圆形山谷，在x轴方向上坡度平缓，而在y轴方向上坡度陡峭

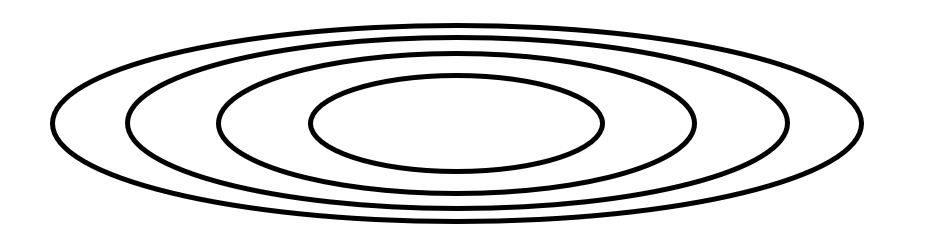
相较于图中任意一条封闭椭圆等值线上的点，椭圆外的点函数值更大，而椭圆内的点函数值更小，因此一条直线上函数值最小的点必然是该直线与某个等值线的切点。这意味着，除非起点的梯度方向与y轴平行，否则最速下降法的迭代结果无法停留在y轴方向上的最低点

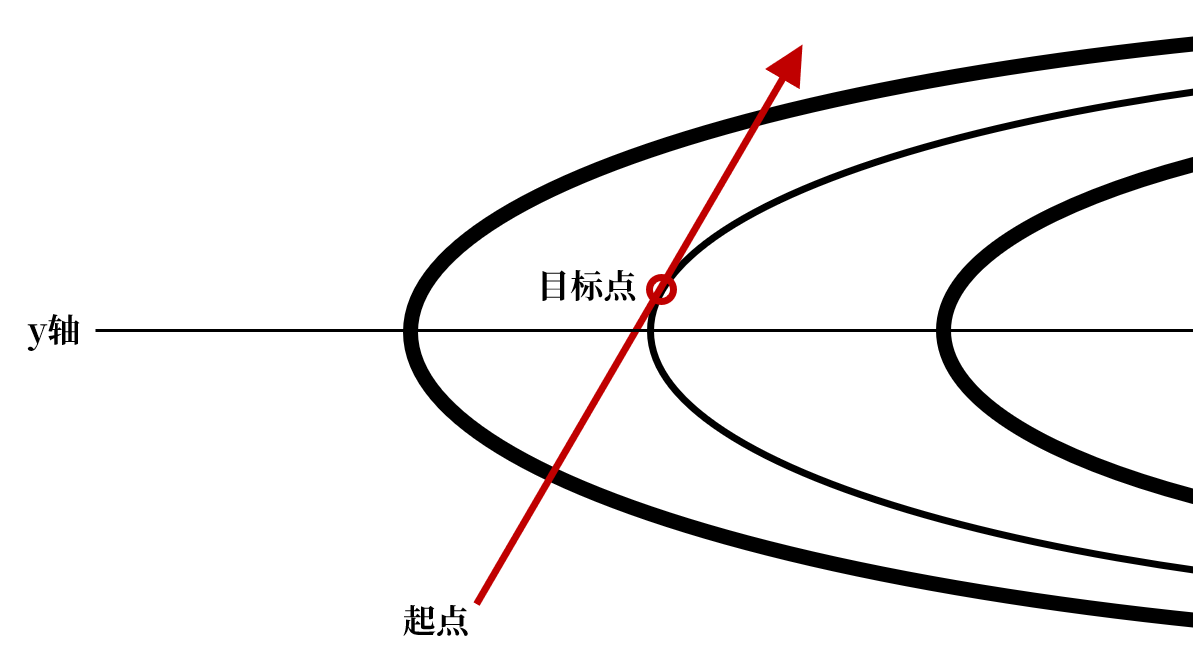
由此，最速下降法的更新便会不断围绕y轴振荡，这将大大降低更新效率。

共轭梯度法的核心在于共轭方向。我们都知道，一对正交向量满足$u^{T}v=0$，它们在欧氏几何意义下是相互垂直的。如果我们对空间进行一个线性变换$A$，则这对向量将满足$u^{T}Av=0$，即关于$A$共轭。根据这一点，如果我们把椭圆视为是由圆经过$A$变换而来的，先按照最速下降法找到等值线上一点及其在该点上的切线方向，再沿着由$A$定义的与之共轭的方向搜索，就能直接到达函数值最小的中心点

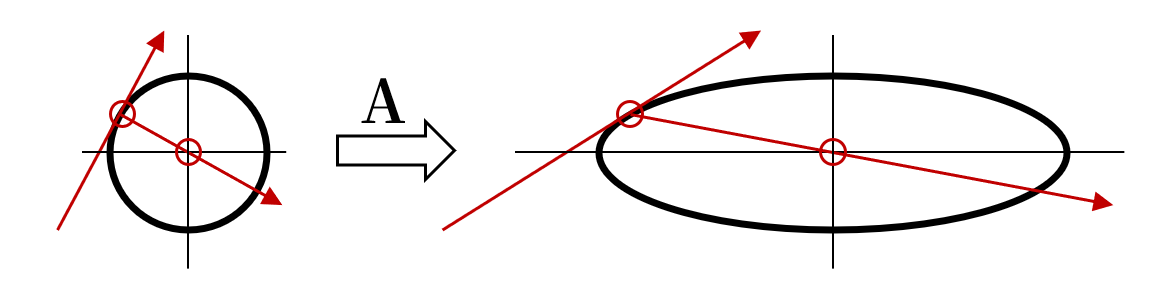
在精确算术运算下，对于$n$维空间，共轭梯度法最多经过$n$次迭代就能得到精确解。本文不进一步展开其具体迭代步骤。最终，对于共轭梯度法给出的更新方向$x$，我们根据KL散度约束计算出一个缩放因子

$$\alpha =\sqrt{\frac{2\delta }{x^T\bar{F}x}}$$

则参数更新为

$$\theta \leftarrow \theta +\alpha \cdot x$$

广义优势估计

TRPO采用广义优势估计计算优势函数。优势函数的原始定义为

$$A(s,a)=Q(s,a)-V(s)$$

如果使用$n$步回报对其进行估计，则有

$$A^{(n)}(s_t,a_t)=\sum _{k=0}^{n-1}{\gamma }^k{r}_{t+k}+{\gamma }^{n}V(s_{t+n})-V(s_t)$$

广义优势估计应用了TD(λ)的思想，即不选择一个固定的$n$，而是将所有$n$步的估计通过一个权重$\lambda$进行指数加权平均，从而结合了所有步长的信息，平衡偏差和方差

$$A(s_t,a_t)=(1-\lambda )A^{(1)}(s_t,a_t)+\lambda A^{(2)}(s_t,a_t)+{\lambda }^2{A}^{(3)}(s_t,a_t)+\cdots$$

我们可以通过单步TD误差对其进行化简

$$\begin{array}{r}{\delta }_t=r_t+\gamma V(s_{t+1})-V(s_t)\\ A(s_t,a_t)=\sum _{k=0}^T(\gamma \lambda {)}^k{\delta }_{t+k}\end{array}$$

算法流程

1. 初始化Actor网络参数$\theta$，Critic V网络参数$w$，信任区域阈值$\delta$；
2. 循环：
   1. 使用当前策略${\pi }_{\theta }$与环境交互，收集一组轨迹的数据$\mathcal{D}$；
   2. 利用数据$\mathcal{D}$得到的TD误差更新Critic网络$w_{t+1}=w_t-{\alpha }_w{\delta }_t\cdot {\nabla }_w{V}_w(s_t)$；
   3. 计算数据$\mathcal{D}$中所有状态-动作对的广义优势估计$A(s_t,a_t)$；
   4. 构建并求解优化问题以更新Actor网络$\theta \leftarrow \theta +\alpha \cdot x$；
   5. 丢弃数据$\mathcal{D}$，进入下一轮迭代；
3. 直到Actor网络和Critic网络收敛。

PPO

TRPO的弊端显而易见，其求解优化问题的计算过于复杂，而且需要采样整个状态空间来估计KL散度的期望。PPO（Proximal Policy Optimization，近端策略优化）则专注于简化训练过程，在克服TRPO的计算复杂性的同时保证训练效果。

剪辑目标函数

PPO采用了更简单的方法限制策略更新幅度，其主要通过概率比衡量新旧策略的差异

$$r(\theta )=\frac{{\pi }_{\theta }(a|s)}{{\pi }_{\mathrm{old}}(a|s)}$$

PPO在目标函数中直接对其进行裁剪操作

$$L_{\mathrm{CLIP}}(\theta )={\mathbb{E}}_{{\pi }_{\mathrm{old}}}[\min (r(\theta )A,\mathrm{clip}(r(\theta ),1-ϵ,1+ϵ)A)]$$

（在PPO上下文中目标函数使用L）

裁剪操作会将$r(\theta )$限制在$[1-ϵ,1+ϵ]$的范围内。如果优势函数$A>0$，我们则希望增加这个动作的概率，即$r(\theta )>1$，但会被限制在$1+ϵ$以下；反之如果$A<0$，我们则希望$r(\theta )<1$，但会被限制在$1-ϵ$以上。

现在我们来计算剪辑目标函数的梯度。如果$r(\theta )$没有触发裁剪操作，则其梯度为

$$\begin{array}{rl}{\nabla }_{\theta }{L}_{\mathrm{CLIP}}& ={\nabla }_{\theta }{\mathbb{E}}_{{\pi }_{\mathrm{old}}}[r(\theta )A]\\ & ={\mathbb{E}}_{{\pi }_{\mathrm{old}}}\left[{\nabla }_{\theta }\frac{{\pi }_{\theta }(a|s)}{{\pi }_{\mathrm{old}}(a|s)}{A}_{{\pi }_{\mathrm{old}}}(s,a)\right]\\ & ={\mathbb{E}}_{{\pi }_{\mathrm{old}}}\left[\frac{{\nabla }_{\theta }{\pi }_{\theta }(a|s)}{{\pi }_{\mathrm{old}}(a|s)}{A}_{{\pi }_{\mathrm{old}}}(s,a)\right]\\ & ={\mathbb{E}}_{{\pi }_{\mathrm{old}}}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{\mathrm{old}}(a|s)}\frac{{\nabla }_{\theta }{\pi }_{\theta }(a|s)}{{\pi }_{\theta }(a|s)}{A}_{{\pi }_{\mathrm{old}}}(s,a)\right]\\ & ={\mathbb{E}}_{{\pi }_{\mathrm{old}}}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{\mathrm{old}}(a|s)}{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)A_{{\pi }_{\mathrm{old}}}(s,a)\right]\end{array}$$

如果$r(\theta )$超出阈值触发了裁剪操作，则其会被修正为一个常数，因而梯度为零。

熵正则化

为了鼓励策略探索，避免其在学习过程中降低方差，PPO引入了熵正则化项

$$L_{\mathrm{ENT}}(\theta )={\mathbb{E}}_{s\sim {\pi }_{\theta }}[\mathcal{H}({\pi }_{\theta }(\cdot |s))]$$

其中$\mathcal{H}(\pi (\cdot |s))$是策略$\pi$在状态$s$下的熵

$$\begin{array}{rl}\mathcal{H}(\pi (\cdot |s))& =-{\mathbb{E}}_{a\sim \pi }[\log \pi (a|s)]\\ & =-\int \pi (a|s)\log \pi (a|s)\mathrm{d}a\end{array}$$

观察$-x\log x$（以2为底）的函数图像，可知最大化策略的熵的效果就是让动作的概率向“中间”靠拢，即趋于均匀分布。随着底数的增大，函数的极值将变小，最大化目标对策略随机性的激励强度也将变小。

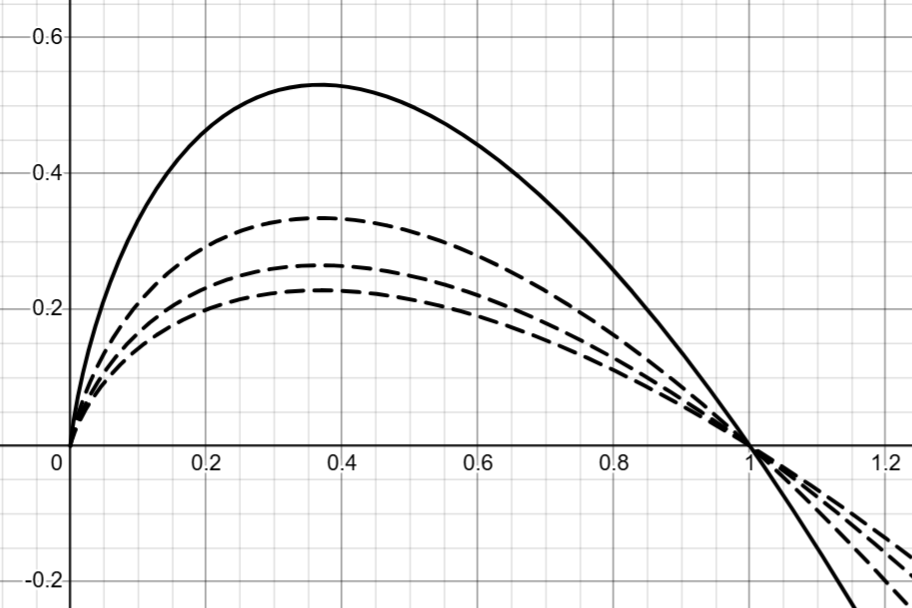
在应用熵正则化项时我们会为其赋予一个权重系数$c$。根据对数换底公式，熵正则化中底数的影响可以被吸收进$c$中。$c$越大，目标越鼓励策略的随机性，而底数在实际实现中通常采用自然常数$e$。

现在我们来计算熵正则化的梯度，对于期望内部有

$$\begin{array}{rl}{\nabla }_{\theta }\mathcal{H}({\pi }_{\theta }(\cdot |s))& =-{\nabla }_{\theta }\int {\pi }_{\theta }(a|s)\log {\pi }_{\theta }(a|s)\mathrm{d}a\\ & =-\int ({\nabla }_{\theta }{\pi }_{\theta }(a|s)\cdot \log {\pi }_{\theta }(a|s)+{\pi }_{\theta }(a|s)\cdot {\nabla }_{\theta }{\pi }_{\theta }(a|s))\mathrm{d}a\\ & =-\int ({\pi }_{\theta }(a|s){\nabla }_{\theta }\log {\pi }_{\theta }(a|s)\cdot \log {\pi }_{\theta }(a|s)+{\pi }_{\theta }(a|s)\cdot {\nabla }_{\theta }{\pi }_{\theta }(a|s))\mathrm{d}a\\ & =-\int {\pi }_{\theta }(a|s){\nabla }_{\theta }\log {\pi }_{\theta }(a|s)(\log {\pi }_{\theta }(a|s)+1)\mathrm{d}a\\ & =-{\mathbb{E}}_{a\sim {\pi }_{\theta }}[(1+\log {\pi }_{\theta }(a|s)){\nabla }_{\theta }\log {\pi }_{\theta }(a|s)]\end{array}$$

则

$$\begin{array}{rl}{\nabla }_{\theta }{L}_{\mathrm{E}NT}(\theta )& ={\mathbb{E}}_{s\sim {\pi }_{\theta }}[{\nabla }_{\theta }\mathcal{H}({\pi }_{\theta }(\cdot |s))]\\ & =-{\mathbb{E}}_{s\sim {\pi }_{\theta }}[{\mathbb{E}}_{a\sim {\pi }_{\theta }}[(1+\log {\pi }_{\theta }(a|s)){\nabla }_{\theta }\log {\pi }_{\theta }(a|s)]]\\ & =-{\mathbb{E}}_{(s,a)\sim {\pi }_{\theta }}[(1+\log {\pi }_{\theta }(a|s)){\nabla }_{\theta }\log {\pi }_{\theta }(a|s)]\end{array}$$

总损失函数

PPO值函数的更新方式即最小化均方蒙特卡洛误差

$$L_{\mathrm{VF}}(\theta )={\mathbb{E}}_{s\sim {\pi }_{\theta }}[(V_w(s_t)-G_t{)}^2]$$

PPO在实现中将所有损失函数和目标函数合并为一个总损失函数

$$L=L_{\mathrm{CLIP}}+c_1{L}_{\mathrm{ENT}}-c_2{L}_{\mathrm{VF}}$$

其中权重系数$c_1$和$c_2$用于平衡三者的更新。

由此，代码可以简洁地使用同一个优化器和同一次反向传播来更新所有参数，同时可以实现策略网络和价值网络共享底层的特征提取层，提升学习效率。

算法流程

在其他技术细节上，PPO结合了A2C的多智能体并行和DQN的经验回放，最终完整的算法流程如下：

1. 初始化Actor网络参数$\theta$，Critic V网络参数$w$；
2. 超参数：裁剪阈值$ϵ$，权重系数$c_1$和$c_2$，广义优势估计权重$\lambda$；
3. 循环：
   1. 使用当前策略${\pi }_{\theta }$在环境中并行运行$N$个智能体，收集$T$个时间步的数据并存入经验缓冲区；
   2. 对于缓冲区中的每个时间步$t$，计算累积回报$G_t$和广义优势估计$A(s_t,a_t)$；
   3. 将整个缓冲区视为一个数据集，随机打乱后分成小批量；
   4. 对每个小批量重复$K$次：
      1. 计算概率比$r_t(\theta )$；
      2. 计算组合目标函数$L(\theta )$；
      3. 根据梯度同时更新参数$\theta$和$w$；
   5. 将参数$\theta$同步到当前策略，进入下一轮迭代；
4. 直到Actor网络和Critic网络收敛。