构建AI智能体:八十三、当AI开始“失忆“:深入理解和预防模型衰老与数据漂移
一、前言
当AI也开始落伍了,想象一下,一位在2020年训练出来的医疗诊断专家,在2024年仍然使用当时的医学知识进行诊断,这就是大模型在生产环境中面临的残酷现实,模型衰老和数据漂移。这两个隐形杀手正在悄无声息地侵蚀着AI系统的价值,这不仅是技术层面的挑战,更是影响AI落地成效的关键因素。
模型衰老,指的是训练好的模型随时间推移性能逐渐衰减的过程,就像知识会过时一样,模型在训练阶段学到的模式与规律,在面对持续变化的现实世界时,其预测能力会自然衰退。这种衰退往往难以察觉,却对业务产生深远影响:推荐系统的点击率悄然下降,风控模型的误报率默默上升,预测系统的准确度逐步走低。
数据漂移则是模型衰老的主要推手。它表现为模型输入数据的统计分布随时间发生变化,导致训练数据与生产环境数据出现显著差异。数据漂移可分为三种类型:协变量漂移,即输入特征分布变化;概念漂移,指输入输出关系发生变化;先验概率漂移,表示目标变量分布改变。在快速变化的商业环境中,用户行为模式、市场竞争格局、产品功能特性都在持续演进,这些变化最终都会体现在数据层面,引发不同程度的数据漂移。
理解并应对模型衰老与数据漂移,已成为现代机器学习系统运维的核心课题。这不仅需要技术层面的监控与干预,更需要建立系统化的管理流程和预警机制。只有主动识别这些隐形威胁,才能确保AI系统持续创造价值,避免智能系统退化为过时工具的命运。

二、模型衰老
1. 基础说明
简单理解:如同人类的专业知识会过时,好比医生毕业多年后,医学知识没有更新,诊断方法变得过时,通常表现为模型的预测准确率随时间推移逐渐下降
技术定义:模型部署后,其参数和决策边界固定不变,但世界在变化,模型性能随时间推移而自然衰减的现象,即使数据分布保持不变,由于业务环境、用户行为等外部因素变化,模型的预测能力逐渐下降。
2. 场景模拟
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseprint("模型衰老通俗演示:音乐推荐系统的故事")
print("=" * 50)# 故事背景:一个音乐推荐模型,预测用户喜欢什么风格的音乐
# 特征:用户年龄、听歌时间段、设备类型
# 目标:是否喜欢流行音乐(1=喜欢, 0=不喜欢)# 初始训练数据(2022年)
print("\n场景1:2022年训练模型(模型年轻时期)")
print("-" * 40)np.random.seed(42)
n_samples = 2000# 生成2022年训练数据
def generate_2022_data(n):"""生成2022年的用户数据"""ages = np.random.normal(25, 8, n) # 用户平均年龄25岁listen_time = np.random.normal(20, 6, n) # 晚上8点听歌device_type = np.random.choice([0, 1], n, p=[0.7, 0.3]) # 70%用手机# 2022年的音乐偏好规则:年轻人喜欢流行音乐pop_prob = 1 / (1 + np.exp(-(0.1*ages - 0.05*listen_time + 0.8*device_type - 1.5)))likes_pop = np.random.binomial(1, pop_prob)return np.column_stack([ages, listen_time, device_type]), likes_popX_2022, y_2022 = generate_2022_data(n_samples)print("2022年数据特征:")
print(f"用户平均年龄:{X_2022[:, 0].mean():.1f}岁")
print(f"主要听歌时间:晚上{X_2022[:, 1].mean():.0f}点")
print(f"手机用户比例:{X_2022[:, 2].mean():.1%}")
print(f"喜欢流行音乐比例:{y_2022.mean():.1%}")# 训练初始模型
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X_2022, y_2022)# 在训练数据上的表现
train_accuracy = accuracy_score(y_2022, model.predict(X_2022))
print(f"模型在2022年数据上的准确率:{train_accuracy:.1%}")# 模拟2023-2025年的数据变化和模型表现
print("\n场景2:2023-2025年模型表现跟踪")
print("-" * 40)years = [2023, 2024, 2025]
accuracies = []
user_trends = []for year in years:# 每年用户习惯都在变化years_passed = year - 2022# 生成当年的测试数据n_test = 500# 用户群体在变化:年龄增长,听歌时间变化current_ages = np.random.normal(25 + years_passed, 8, n_test)current_listen_time = np.random.normal(20 - years_passed*0.5, 6, n_test) # 听歌时间提前current_device = np.random.choice([0, 1], n_test, p=[0.7 - years_passed*0.1, 0.3 + years_passed*0.1]) # 更多用手机# 音乐偏好也在变化:流行音乐的定义在变# 模型衰老的关键:现实规则变了,但模型还记着老规则if year == 2023:# 2023年:开始有些变化pop_prob = 1 / (1 + np.exp(-(0.09*current_ages - 0.04*current_listen_time + 0.9*current_device - 1.3)))elif year == 2024:# 2024年:变化更明显pop_prob = 1 / (1 + np.exp(-(0.08*current_ages - 0.03*current_listen_time + 1.0*current_device - 1.1)))else:# 2025年:完全不同的规则pop_prob = 1 / (1 + np.exp(-(0.06*current_ages - 0.02*current_listen_time + 1.2*current_device - 0.8)))y_current = np.random.binomial(1, pop_prob)X_current = np.column_stack([current_ages, current_listen_time, current_device])# 用老模型预测新数据y_pred = model.predict(X_current)accuracy = accuracy_score(y_current, y_pred)accuracies.append(accuracy)user_trends.append({'year': year,'avg_age': current_ages.mean(),'avg_listen_time': current_listen_time.mean(),'mobile_ratio': current_device.mean(),'pop_ratio': y_current.mean(),'accuracy': accuracy})print(f"{year}年 - 准确率: {accuracy:.1%} | "f"用户年龄: {current_ages.mean():.1f}岁 | "f"听歌时间: 晚上{current_listen_time.mean():.0f}点")# 可视化模型衰老过程
plt.figure(figsize=(15, 10))# 子图1:准确率衰减趋势
plt.subplot(2, 3, 1)
years_display = [2022] + years
accuracies_display = [train_accuracy] + accuraciesplt.plot(years_display, accuracies_display, 'ro-', linewidth=3, markersize=8)
plt.axhline(y=0.7, color='red', linestyle='--', alpha=0.7, label='性能警戒线')
plt.xlabel('年份')
plt.ylabel('模型准确率')
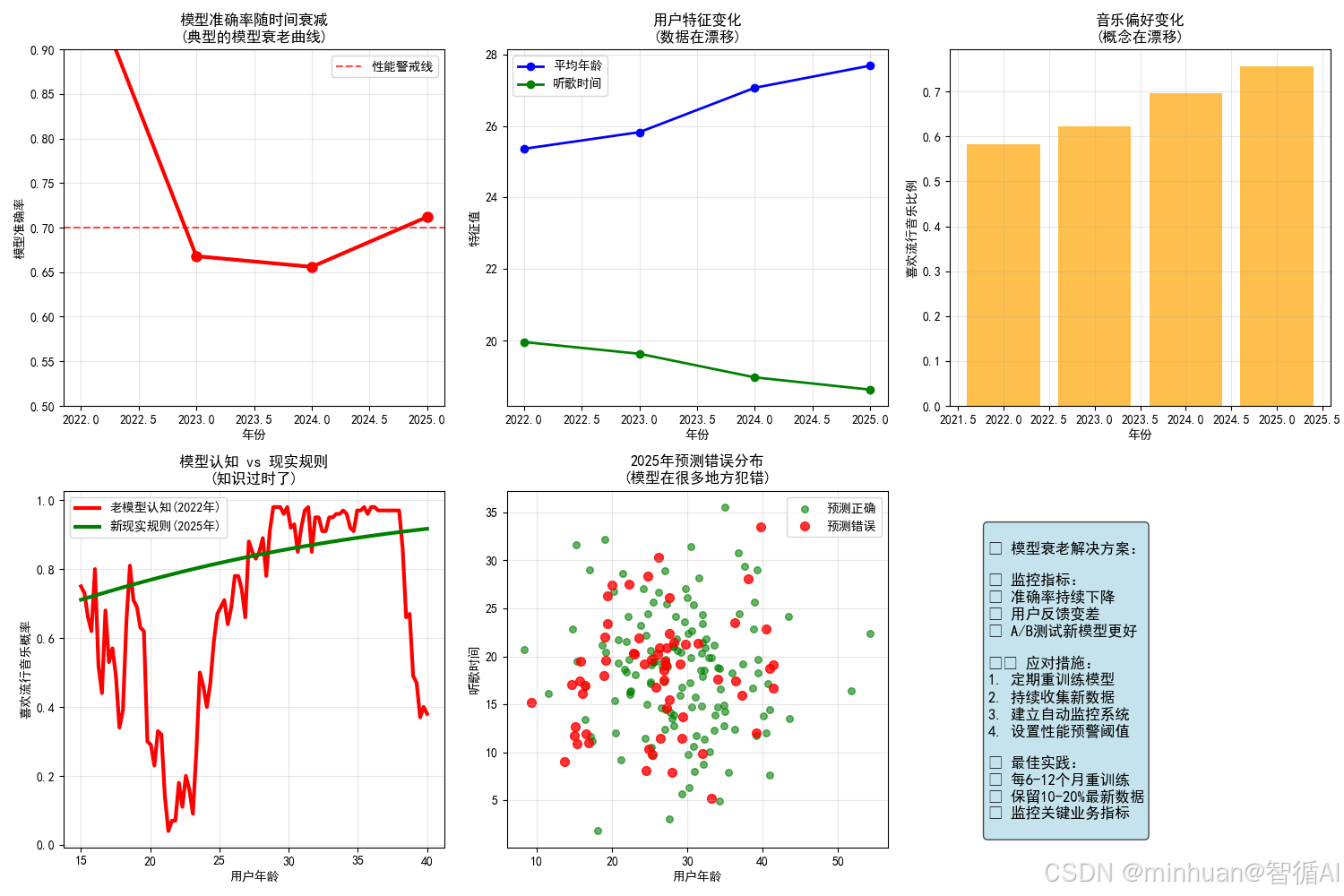
plt.title('模型准确率随时间衰减\n(典型的模型衰老曲线)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.ylim(0.5, 0.9)# 子图2:用户特征变化
plt.subplot(2, 3, 2)
user_ages = [X_2022[:, 0].mean()] + [trend['avg_age'] for trend in user_trends]
listen_times = [X_2022[:, 1].mean()] + [trend['avg_listen_time'] for trend in user_trends]plt.plot(years_display, user_ages, 'bo-', label='平均年龄', linewidth=2)
plt.plot(years_display, listen_times, 'go-', label='听歌时间', linewidth=2)
plt.xlabel('年份')
plt.ylabel('特征值')
plt.title('用户特征变化\n(数据在漂移)')
plt.legend()
plt.grid(True, alpha=0.3)# 子图3:音乐偏好变化
plt.subplot(2, 3, 3)
pop_ratios = [y_2022.mean()] + [trend['pop_ratio'] for trend in user_trends]plt.bar(years_display, pop_ratios, color='orange', alpha=0.7)
plt.xlabel('年份')
plt.ylabel('喜欢流行音乐比例')
plt.title('音乐偏好变化\n(概念在漂移)')
plt.grid(True, alpha=0.3)# 子图4:模型决策边界对比
plt.subplot(2, 3, 4)
# 模拟不同年龄用户的偏好变化
test_ages = np.linspace(15, 40, 100)
test_features = np.column_stack([test_ages,np.full(100, 20), # 固定听歌时间np.ones(100) # 都用手机
])# 老模型的预测
old_predictions = model.predict_proba(test_features)[:, 1]# 假设的新规则(2025年)
new_rules_prob = 1 / (1 + np.exp(-(0.06*test_ages - 0.02*20 + 1.2*1 - 0.8)))plt.plot(test_ages, old_predictions, 'r-', linewidth=3, label='老模型认知(2022年)')
plt.plot(test_ages, new_rules_prob, 'g-', linewidth=3, label='新现实规则(2025年)')
plt.xlabel('用户年龄')
plt.ylabel('喜欢流行音乐概率')
plt.title('模型认知 vs 现实规则\n(知识过时了)')
plt.legend()
plt.grid(True, alpha=0.3)# 子图5:错误类型分析
plt.subplot(2, 3, 5)
# 分析2025年的预测错误
X_2025 = np.column_stack([np.random.normal(28, 8, 200),np.random.normal(18.5, 6, 200),np.random.choice([0, 1], 200, p=[0.5, 0.5])
])pop_prob_2025 = 1 / (1 + np.exp(-(0.06*X_2025[:, 0] - 0.02*X_2025[:, 1] + 1.2*X_2025[:, 2] - 0.8)))
y_2025 = np.random.binomial(1, pop_prob_2025)
y_pred_2025 = model.predict(X_2025)errors = y_pred_2025 != y_2025
correct = ~errorsplt.scatter(X_2025[correct, 0], X_2025[correct, 1], c='green', alpha=0.6, label='预测正确', s=30)
plt.scatter(X_2025[errors, 0], X_2025[errors, 1], c='red', alpha=0.8, label='预测错误', s=50)plt.xlabel('用户年龄')
plt.ylabel('听歌时间')
plt.title('2025年预测错误分布\n(模型在很多地方犯错)')
plt.legend()
plt.grid(True, alpha=0.3)# 子图6:解决方案
plt.subplot(2, 3, 6)
plt.axis('off')
solution_text = """
模型衰老解决方案:监控指标:
• 准确率持续下降
• 用户反馈变差
• A/B测试新模型更好应对措施:
1. 定期重训练模型
2. 持续收集新数据
3. 建立自动监控系统
4. 设置性能预警阈值最佳实践:
• 每6-12个月重训练
• 保留10-20%最新数据
• 监控关键业务指标
"""plt.text(0.1, 0.9, solution_text, fontsize=12, verticalalignment='top',bbox=dict(boxstyle="round,pad=0.3", facecolor="lightblue", alpha=0.7))plt.tight_layout()
plt.show()# 详细分析
print(f"\n模型衰老分析报告")
print("=" * 50)print(f"\n性能衰减详情:")
for i, year in enumerate(years):decline = train_accuracy - accuracies[i]print(f"{year}年:准确率 {accuracies[i]:.1%} (下降 {decline:.1%})")print(f"\n用户行为变化:")
print("• 用户年龄增长:音乐品味在成熟")
print("• 听歌时间提前:生活习惯在改变")
print("• 更多手机用户:设备偏好变化")
print("• 流行音乐定义:音乐趋势在演进")print(f"\n模型衰老的根本原因:")
print("1. 知识过时:模型还记着2022年的规则")
print("2. 环境变化:用户行为和音乐趋势都在变")
print("3. 时间效应:模型没有持续学习新知识")
print("4. 规则演变:喜欢流行音乐的标准变了")print(f"\n业务影响:")
print("• 推荐质量下降 → 用户满意度降低")
print("• 错过新趋势 → 商业机会流失")
print("• 用户体验变差 → 用户流失风险")print(f"\n验证解决方案:")
# 用2025年数据重新训练
new_model = RandomForestClassifier(n_estimators=100, random_state=42)
new_model.fit(X_2025, y_2025)
new_accuracy = accuracy_score(y_2025, new_model.predict(X_2025))print(f"老模型在2025年准确率:{accuracies[-1]:.1%}")
print(f"新模型在2025年准确率:{new_accuracy:.1%}")
print(f"重训练提升:{new_accuracy - accuracies[-1]:.1%}")print(f"\n关键结论:模型像食物一样会'过期',需要定期'保鲜'!")
模型衰老通俗演示:音乐推荐系统的故事
==================================================
场景1:2022年训练模型(模型年轻时期)
----------------------------------------
2022年数据特征:
- 用户平均年龄:25.4岁
- 主要听歌时间:晚上20点
- 手机用户比例:29.5%
- 喜欢流行音乐比例:58.2%
- 模型在2022年数据上的准确率:100.0%
场景2:2023-2025年模型表现跟踪
----------------------------------------
2023年 - 准确率: 66.8% | 用户年龄: 25.8岁 | 听歌时间: 晚上20点
2024年 - 准确率: 65.6% | 用户年龄: 27.1岁 | 听歌时间: 晚上19点
2025年 - 准确率: 71.2% | 用户年龄: 27.7岁 | 听歌时间: 晚上19点
模型衰老分析报告
==================================================
性能衰减详情:
- 2023年:准确率 66.8% (下降 33.1%)
- 2024年:准确率 65.6% (下降 34.4%)
- 2025年:准确率 71.2% (下降 28.8%)
用户行为变化:
- 用户年龄增长:音乐品味在成熟
- 听歌时间提前:生活习惯在改变
- 更多手机用户:设备偏好变化
- 流行音乐定义:音乐趋势在演进
模型衰老的根本原因:
- 1.知识过时:模型还记着2022年的规则
- 2.环境变化:用户行为和音乐趋势都在变
- 3.时间效应:模型没有持续学习新知识
- 4.规则演变:喜欢流行音乐的标准变了
业务影响:
- 推荐质量下降 → 用户满意度降低
- 错过新趋势 → 商业机会流失
- 用户体验变差 → 用户流失风险
验证解决方案:
- 老模型在2025年准确率:71.2%
- 新模型在2025年准确率:100.0%
- 重训练提升:28.8%
关键结论:模型像食物一样会'过期',需要定期'保鲜'!
三. 数据漂移
1. 基础概念
简单理解:世界在变,但模型的认知还停留在过去,好比疾病本身发生了变异,出现了新的症状,但医生还在用老方法诊断
技术定义:模型输入数据的统计属性随时间发生变化,导致训练数据与推理数据分布不一致。
数据漂移的两种主要类型:
1.1 协变量漂移
输入特征X的分布P(X)发生变化,但条件分布P(Y|X)保持不变,比如用户行为模式改变
协变量漂移公式:
- P_train(X) ≠ P_production(X)
- P_train(Y|X) = P_production(Y|X)
通俗解释:输入数据的长相变了,但它们的含义没变。就像顾客的年龄分布从年轻人为主变成了中年人为主,但每个年龄段的购买习惯没变。
例子:用户画像特征分布变化,但购买行为逻辑不变
1.2 概念漂移
输入输出关系P(Y|X)发生变化,同样的特征,含义不同了
概念漂移公式:
- P_train(Y|X) ≠ P_production(Y|X)
通俗解释:同样的输入特征,现在代表不同的含义了。比如同样的收入水平,在经济繁荣期代表高消费意愿,在经济衰退期代表保守消费。
例子:同样的用户特征,在疫情前后代表不同的购买意愿
2. 漂移检测指标
2.1 PSI-群体稳定性指标
2.1.1 基本概念
- 定义:用于衡量两个群体在特征分布上的差异程度。
- 核心思想:通过比较不同时间段或不同群体在相同特征上的分布差异,来判断数据是否发生显著变化。
2.1.2 PSI的数学推导
- PSI = Σ [ (A_i - E_i) × ln(A_i / E_i) ]
- 其中:
- A_i = 当前数据在第i个分桶的占比,实际占比
- E_i = 参考数据在第i个分桶的占比,预期占比
- PSI基于KL散度,衡量两个概率分布的差异。
2.1.3 PSI判断标准
- PSI < 0.1:无明显漂移,分布基本稳定,建议继续监控
- 0.1 ≤ PSI < 0.25:轻微漂移,分布有些变化,需要关注
- PSI ≥ 0.25:显著漂移,分布明显不同,需要立即处理
2.1.4 PSI计算完整演示
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseclass PSICalculator:"""PSI计算器完整实现"""def __init__(self, num_bins=10, smooth_factor=0.0001):"""初始化PSI计算器参数:num_bins: 分桶数量smooth_factor: 平滑因子,避免除零错误"""self.num_bins = num_binsself.smooth_factor = smooth_factordef create_breakpoints(self, reference_data):"""创建分桶边界点基于参考数据的分位数创建分桶,确保每个桶有大致相同的数据量"""# 计算分位点 (0%, 10%, 20%, ..., 100%)percentiles = np.linspace(0, 100, self.num_bins + 1)breakpoints = np.percentile(reference_data, percentiles)# 扩展首尾以包含可能的异常值breakpoints[0] = -np.infbreakpoints[-1] = np.infprint(f"分桶边界点: {breakpoints}")return breakpointsdef calculate_bucket_percentages(self, data, breakpoints):"""计算每个分桶的数据占比"""# 计算每个桶的数据量counts, _ = np.histogram(data, bins=breakpoints)# 转换为占比percentages = counts / len(data)# 平滑处理:避免零值percentages = np.where(percentages == 0, self.smooth_factor, percentages)# 重新归一化,确保总和为1percentages = percentages / np.sum(percentages)return percentagesdef calculate_single_psi(self, expected_perc, actual_perc):"""计算单个特征的PSI值"""# PSI计算公式: Σ[(实际占比 - 预期占比) * ln(实际占比/预期占比)]psi_components = (actual_perc - expected_perc) * np.log(actual_perc / expected_perc)total_psi = np.sum(psi_components)return total_psi, psi_componentsdef calculate_psi(self, reference_data, current_data, feature_name=None):"""计算PSI值 - 主函数参数:reference_data: 参考数据(训练数据)current_data: 当前数据(生产数据)feature_name: 特征名称(用于输出)"""print(f"\n 开始计算PSI值{' - ' + feature_name if feature_name else ''}")print("=" * 60)# 步骤1: 数据基础统计print("步骤1: 数据基础统计")print(f"参考数据: 数量={len(reference_data)}, 均值={np.mean(reference_data):.3f}, 标准差={np.std(reference_data):.3f}")print(f"当前数据: 数量={len(current_data)}, 均值={np.mean(current_data):.3f}, 标准差={np.std(current_data):.3f}")# 步骤2: 创建分桶边界(基于参考数据)print("\n步骤2: 创建分桶边界")breakpoints = self.create_breakpoints(reference_data)# 步骤3: 计算各桶占比print("\n步骤3: 计算各桶占比")expected_perc = self.calculate_bucket_percentages(reference_data, breakpoints)actual_perc = self.calculate_bucket_percentages(current_data, breakpoints)# 输出各桶占比详情print("\n各桶占比详情:")print("桶号 | 参考数据占比 | 当前数据占比 | 差值")print("-" * 50)for i in range(self.num_bins):diff = actual_perc[i] - expected_perc[i]print(f"{i+1:2} | {expected_perc[i]:.4f} | {actual_perc[i]:.4f} | {diff:+.4f}")# 步骤4: 计算PSI值print("\n步骤4: 计算PSI值")total_psi, psi_components = self.calculate_single_psi(expected_perc, actual_perc)# 输出PSI分量详情print("\nPSI分量计算:")print("桶号 | (A-E) | ln(A/E) | PSI分量")print("-" * 40)for i in range(self.num_bins):a_minus_e = actual_perc[i] - expected_perc[i]ln_a_e = np.log(actual_perc[i] / expected_perc[i])psi_component = psi_components[i]print(f"{i+1:2} | {a_minus_e:+.4f} | {ln_a_e:+.4f} | {psi_component:.6f}")# 步骤5: 结果解释print(f"\n步骤5: 结果解释")print(f"总PSI值: {total_psi:.6f}")self.interpret_psi(total_psi)# 返回详细结果result = {'total_psi': total_psi,'psi_components': psi_components,'expected_percentages': expected_perc,'actual_percentages': actual_perc,'breakpoints': breakpoints,'drift_level': self.get_drift_level(total_psi)}return resultdef interpret_psi(self, psi_value):"""解释PSI值的含义"""print(f"\n PSI值解释:")if psi_value < 0.1:print("✅ 无显著漂移 - 分布基本稳定")print(" 建议: 继续正常监控")elif psi_value < 0.25:print("🟡 轻微漂移 - 分布有些变化")print(" 建议: 加强关注,分析原因")else:print("🔴 显著漂移 - 分布明显不同")print(" 建议: 立即处理,可能需要重训练模型")def get_drift_level(self, psi_value):"""获取漂移等级"""if psi_value < 0.1:return "无漂移"elif psi_value < 0.25:return "轻微漂移"else:return "显著漂移"def visualize_psi_analysis(self, reference_data, current_data, result, feature_name=""):"""可视化PSI分析结果"""fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(15, 12))# 子图1: 数据分布直方图对比ax1.hist(reference_data, bins=20, alpha=0.7, label='参考数据', color='blue')ax1.hist(current_data, bins=20, alpha=0.7, label='当前数据', color='red')ax1.set_xlabel('特征值')ax1.set_ylabel('频数')ax1.set_title(f'{feature_name} - 数据分布对比')ax1.legend()ax1.grid(True, alpha=0.3)# 子图2: 各桶占比对比x_pos = np.arange(len(result['expected_percentages']))width = 0.35ax2.bar(x_pos - width/2, result['expected_percentages'], width, label='参考数据', alpha=0.7, color='blue')ax2.bar(x_pos + width/2, result['actual_percentages'], width, label='当前数据', alpha=0.7, color='red')ax2.set_xlabel('分桶编号')ax2.set_ylabel('数据占比')ax2.set_title('各分桶数据占比对比')ax2.set_xticks(x_pos)ax2.legend()ax2.grid(True, alpha=0.3)# 子图3: PSI分量贡献ax3.bar(range(len(result['psi_components'])), result['psi_components'], color='orange', alpha=0.7)ax3.set_xlabel('分桶编号')ax3.set_ylabel('PSI分量值')ax3.set_title('各分桶对PSI值的贡献')ax3.grid(True, alpha=0.3)# 子图4: PSI结果总结ax4.axis('off')summary_text = f"""
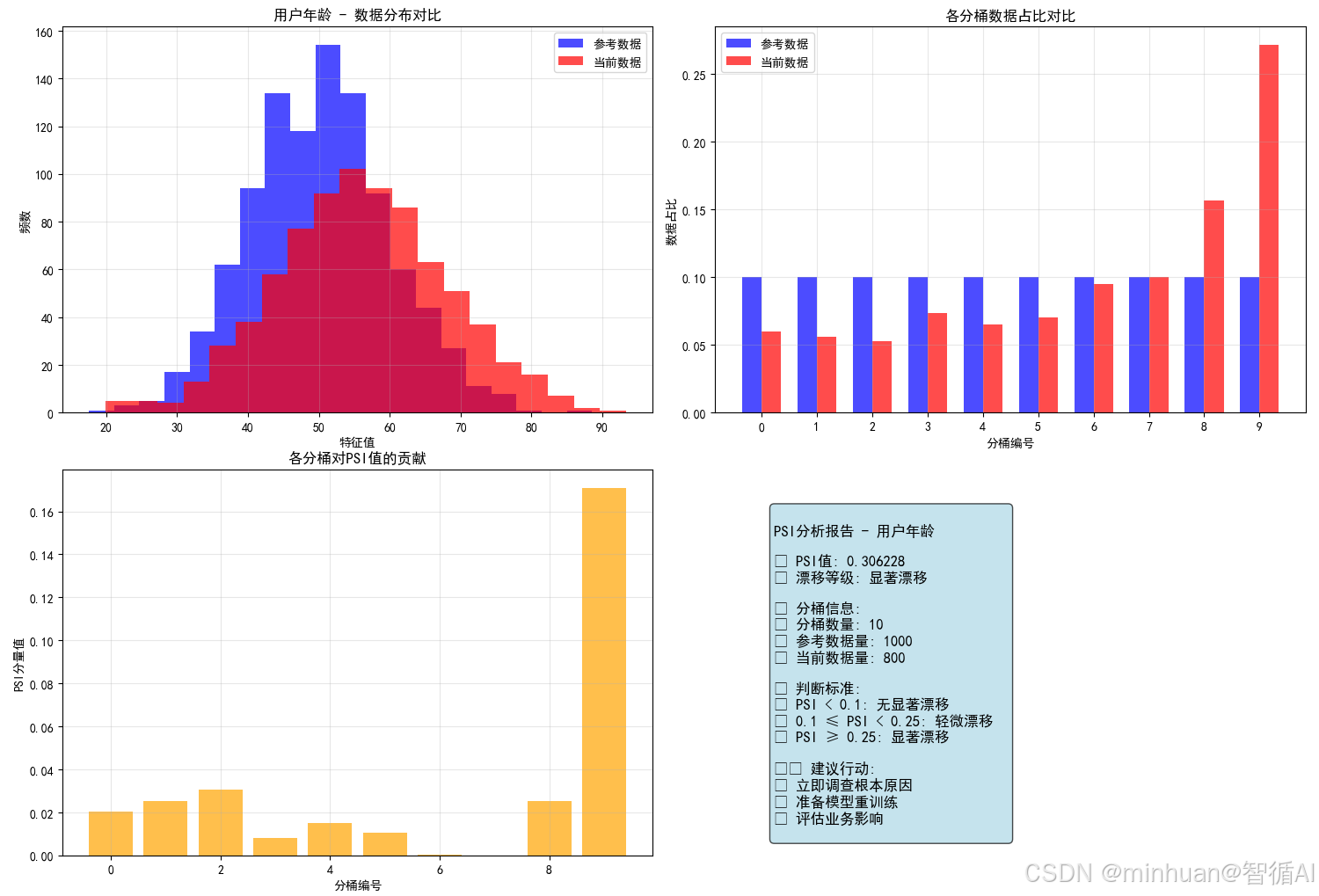
PSI分析报告 - {feature_name}PSI值: {result['total_psi']:.6f}漂移等级: {result['drift_level']}分桶信息:
• 分桶数量: {self.num_bins}
• 参考数据量: {len(reference_data)}
• 当前数据量: {len(current_data)}判断标准:
• PSI < 0.1: 无显著漂移
• 0.1 ≤ PSI < 0.25: 轻微漂移
• PSI ≥ 0.25: 显著漂移建议行动:
{self.get_action_recommendation(result['total_psi'])}
"""ax4.text(0.1, 0.9, summary_text, fontsize=12, verticalalignment='top',bbox=dict(boxstyle="round,pad=0.3", facecolor="lightblue", alpha=0.7))plt.tight_layout()plt.show()def get_action_recommendation(self, psi_value):"""获取行动建议"""if psi_value < 0.1:return "• 继续正常监控\n• 保持当前更新频率"elif psi_value < 0.25:return "• 加强监控频率\n• 分析漂移原因\n• 准备应对方案"else:return "• 立即调查根本原因\n• 准备模型重训练\n• 评估业务影响"# 使用示例
def demonstrate_psi_calculation():"""演示PSI计算全过程"""print("PSI计算完整演示")print("=" * 50)# 创建示例数据np.random.seed(42)# 参考数据(训练期数据)reference_data = np.random.normal(50, 10, 1000) # 均值50,标准差10# 当前数据(生产期数据)- 模拟数据漂移current_data = np.random.normal(55, 12, 800) # 均值漂移到55,标准差变为12# 创建PSI计算器psi_calculator = PSICalculator(num_bins=10)# 计算PSIresult = psi_calculator.calculate_psi(reference_data, current_data, "用户年龄")# 可视化分析psi_calculator.visualize_psi_analysis(reference_data, current_data, result, "用户年龄")return result# 运行演示
if __name__ == "__main__":result = demonstrate_psi_calculation()# 额外测试:不同漂移程度的案例print("\n\n🔬 不同漂移程度案例测试")print("=" * 50)# 案例1:无漂移print("\n案例1: 无漂移情况")ref1 = np.random.normal(50, 10, 1000)curr1 = np.random.normal(50, 10, 1000)psi_calc = PSICalculator()result1 = psi_calc.calculate_psi(ref1, curr1, "无漂移案例")# 案例2:显著漂移print("\n案例2: 显著漂移情况")ref2 = np.random.normal(50, 10, 1000)curr2 = np.random.normal(65, 15, 1000) # 均值和标准差都变化result2 = psi_calc.calculate_psi(ref2, curr2, "显著漂移案例")完整计算过程:
开始计算PSI值 - 用户年龄
============================================================
步骤1: 数据基础统计
- 目的:了解数据的基本情况
- 计算参考数据和当前数据的基础统计量
- 包括数据量、均值、标准差等
- 帮助理解数据变化的整体趋势
参考数据: 数量=1000, 均值=50.193, 标准差=9.787
当前数据: 数量=800, 均值=56.006, 标准差=11.999
步骤2: 创建分桶边界
- 基于参考数据的分位数创建分桶
- 使用np.percentile计算分位点
- 确保每个桶包含大致相同数量的参考数据
- 首尾设置为无穷大以包含异常值
数学原理:
- 分位点计算:0%, 10%, 20%, ..., 100%
- 每个桶包含约10%的参考数据
分桶边界点: [ -inf 37.55236889 41.96518528 44.76641901 47.59310338 50.25300612
52.48685825 55.13981816 58.13511152 63.05645202 inf]
步骤3: 计算各桶占比
- 核心计算:统计每个桶中的数据占比
- 使用np.histogram进行分桶计数
- 转换为比例:占比 = 桶内数据量 / 总数据量
- 平滑处理:避免零值导致的数学错误
平滑处理公式:
- 如果 占比 == 0: 占比 = smooth_factor,示例中为0.0001,避免除零错误
- 然后重新归一化确保总和为1
各桶占比详情:
桶号 | 参考数据占比 | 当前数据占比 | 差值
--------------------------------------------------
1 | 0.1000 | 0.0600 | -0.0400
2 | 0.1000 | 0.0563 | -0.0438
3 | 0.1000 | 0.0525 | -0.0475
4 | 0.1000 | 0.0737 | -0.0263
5 | 0.1000 | 0.0650 | -0.0350
6 | 0.1000 | 0.0700 | -0.0300
7 | 0.1000 | 0.0950 | -0.0050
8 | 0.1000 | 0.1000 | +0.0000
9 | 0.1000 | 0.1562 | +0.0562
10 | 0.1000 | 0.2712 | +0.1712
步骤4: 计算PSI值
核心公式:
- PSI = Σ [ (A_i - E_i) × ln(A_i / E_i) ]
- 其中:
- A_i = 当前数据在第i桶的占比
- E_i = 参考数据在第i桶的占比
计算过程:
- 对每个桶计算 (A_i - E_i)
- 对每个桶计算 ln(A_i / E_i)
- 相乘得到每个桶的PSI分量
- 求和得到总PSI值
PSI分量计算:
桶号 | (A-E) | ln(A/E) | PSI分量
----------------------------------------
1 | -0.0400 | -0.5108 | 0.020433
2 | -0.0438 | -0.5754 | 0.025172
3 | -0.0475 | -0.6444 | 0.030607
4 | -0.0263 | -0.3045 | 0.007993
5 | -0.0350 | -0.4308 | 0.015077
6 | -0.0300 | -0.3567 | 0.010700
7 | -0.0050 | -0.0513 | 0.000256
8 | +0.0000 | +0.0000 | 0.000000
9 | +0.0562 | +0.4463 | 0.025104
10 | +0.1712 | +0.9979 | 0.170885
步骤5: 结果解释
判断标准:
- PSI < 0.1:分布稳定,无需特别处理
- 0.1 ≤ PSI < 0.25:轻微漂移,需要关注
- PSI ≥ 0.25:显著漂移,需要立即处理
总PSI值: 0.306228
PSI值解释:🔴 显著漂移 - 分布明显不同
建议: 立即处理,可能需要重训练模型
不同漂移程度案例测试
===========================================================
案例1: 无漂移情况
开始计算PSI值 - 无漂移案例
============================================================
步骤1: 数据基础统计
参考数据: 数量=1000, 均值=50.100, 标准差=9.683
当前数据: 数量=1000, 均值=49.931, 标准差=10.353
步骤2: 创建分桶边界
分桶边界点: [ -inf 37.62193112 41.81405495 45.0773144 47.67872232 50.03535589
52.80351257 55.3454268 58.11758281 62.31365281 inf]
步骤3: 计算各桶占比
各桶占比详情:
桶号 | 参考数据占比 | 当前数据占比 | 差值
--------------------------------------------------
1 | 0.1000 | 0.1140 | +0.0140
2 | 0.1000 | 0.1100 | +0.0100
3 | 0.1000 | 0.1020 | +0.0020
4 | 0.1000 | 0.0820 | -0.0180
5 | 0.1000 | 0.0950 | -0.0050
6 | 0.1000 | 0.1040 | +0.0040
7 | 0.1000 | 0.1070 | +0.0070
8 | 0.1000 | 0.0680 | -0.0320
9 | 0.1000 | 0.1010 | +0.0010
10 | 0.1000 | 0.1170 | +0.0170
步骤4: 计算PSI值
PSI分量计算:
桶号 | (A-E) | ln(A/E) | PSI分量
----------------------------------------
1 | +0.0140 | +0.1310 | 0.001834
2 | +0.0100 | +0.0953 | 0.000953
3 | +0.0020 | +0.0198 | 0.000040
4 | -0.0180 | -0.1985 | 0.003572
5 | -0.0050 | -0.0513 | 0.000256
6 | +0.0040 | +0.0392 | 0.000157
7 | +0.0070 | +0.0677 | 0.000474
8 | -0.0320 | -0.3857 | 0.012341
9 | +0.0010 | +0.0100 | 0.000010
10 | +0.0170 | +0.1570 | 0.002669
步骤5: 结果解释
总PSI值: 0.022306
PSI值解释:无显著漂移 - 分布基本稳定
建议: 继续正常监控
案例2: 显著漂移情况
开始计算PSI值 - 显著漂移案例
============================================================
步骤1: 数据基础统计
参考数据: 数量=1000, 均值=49.339, 标准差=9.899
当前数据: 数量=1000, 均值=64.651, 标准差=14.815
步骤2: 创建分桶边界
分桶边界点: [ -inf 36.12064049 41.09188218 44.34178165 47.11220006 49.67435643
52.28957524 54.93158582 57.65951219 61.71890351 inf]
步骤3: 计算各桶占比
各桶占比详情:
桶号 | 参考数据占比 | 当前数据占比 | 差值
--------------------------------------------------
1 | 0.1000 | 0.0260 | -0.0740
2 | 0.1000 | 0.0290 | -0.0710
3 | 0.1000 | 0.0300 | -0.0700
4 | 0.1000 | 0.0370 | -0.0630
5 | 0.1000 | 0.0350 | -0.0650
6 | 0.1000 | 0.0350 | -0.0650
7 | 0.1000 | 0.0560 | -0.0440
8 | 0.1000 | 0.0710 | -0.0290
9 | 0.1000 | 0.0970 | -0.0030
10 | 0.1000 | 0.5840 | +0.4840
步骤4: 计算PSI值
PSI分量计算:
桶号 | (A-E) | ln(A/E) | PSI分量
----------------------------------------
1 | -0.0740 | -1.3471 | 0.099683
2 | -0.0710 | -1.2379 | 0.087889
3 | -0.0700 | -1.2040 | 0.084278
4 | -0.0630 | -0.9943 | 0.062638
5 | -0.0650 | -1.0498 | 0.068238
6 | -0.0650 | -1.0498 | 0.068238
7 | -0.0440 | -0.5798 | 0.025512
8 | -0.0290 | -0.3425 | 0.009932
9 | -0.0030 | -0.0305 | 0.000091
10 | +0.4840 | +1.7647 | 0.854130
步骤5: 结果解释
总PSI值: 1.360631
PSI值解释:🔴显著漂移 - 分布明显不同
建议: 立即处理,可能需要重训练模型
2.2. KS检验:比较两个分布的差异程度
2.2.1 基本概念
- 定义:一种非参数统计检验方法,用于检验两个样本是否来自同一分布。
- 核心思想:通过比较两个累积分布函数(CDF)的最大距离来判断分布差异。
2.2.2 KS统计量公式
- D = max|F₁(x) - F₂(x)|
- 其中:
- F₁(x) = 第一个样本的累积分布函数
- F₂(x) = 第二个样本的累积分布函数
- 假设检验框架:
- 零假设H₀:两个样本来自同一分布
- 备择假设H₁:两个样本来自不同分布
- 判断标准:如果p值 < 0.05,拒绝零假设
2.2.3 KS检验的判读标准
- p≥0.05:统计不显著,分布可能相同,置信度低
- 0.05>p≥0.01:统计显著,分布可能不同,置信度一般
- 0.01>p≥0.001:统计很显著,分布很可能不同,置信度高
- p<0.001:统计极其显著,分布肯定不同,置信度很高
2.2.4 KS统计量计算完整演示
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
import warnings
warnings.filterwarnings('ignore')# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseclass KSCalculator:"""KS统计量计算器完整实现"""def __init__(self, alpha=0.05):"""初始化KS计算器参数:alpha: 显著性水平,默认0.05"""self.alpha = alphadef calculate_ecdf(self, data):"""计算经验累积分布函数(ECDF)参数:data: 输入数据数组返回:sorted_data: 排序后的数据ecdf_values: 对应的ECDF值"""# 对数据进行排序sorted_data = np.sort(data)# 计算ECDF值: (i + 1) / n 或 i / n,这里使用i/nn = len(sorted_data)ecdf_values = np.arange(1, n + 1) / nreturn sorted_data, ecdf_valuesdef calculate_ks_statistic(self, data1, data2):"""计算KS统计量参数:data1: 第一组数据(参考数据)data2: 第二组数据(当前数据)返回:ks_statistic: KS统计量max_diff_point: 最大差异点combined_points: 合并的数据点ecdf1_interp: data1在合并点上的ECDF值ecdf2_interp: data2在合并点上的ECDF值"""print("步骤1: 计算两组数据的ECDF")# 计算两组的ECDFsorted_data1, ecdf1 = self.calculate_ecdf(data1)sorted_data2, ecdf2 = self.calculate_ecdf(data2)print(f"数据1: 样本量={len(data1)}, 范围=[{np.min(data1):.3f}, {np.max(data1):.3f}]")print(f"数据2: 样本量={len(data2)}, 范围=[{np.min(data2):.3f}, {np.max(data2):.3f}]")print("\n步骤2: 合并所有数据点")# 合并两组数据的所有点combined_points = np.unique(np.concatenate([sorted_data1, sorted_data2]))print(f"合并后总点数: {len(combined_points)}")print("\n步骤3: 在合并点上插值计算ECDF")# 在合并点上插值计算ECDF值ecdf1_interp = np.interp(combined_points, sorted_data1, ecdf1)ecdf2_interp = np.interp(combined_points, sorted_data2, ecdf2)print("\n步骤4: 计算ECDF差异")# 计算ECDF差异ecdf_diff = np.abs(ecdf1_interp - ecdf2_interp)# 找到最大差异点和对应的KS统计量max_diff_idx = np.argmax(ecdf_diff)ks_statistic = ecdf_diff[max_diff_idx]max_diff_point = combined_points[max_diff_idx]print(f"最大差异点: x = {max_diff_point:.3f}")print(f"ECDF1在最大差异点: {ecdf1_interp[max_diff_idx]:.3f}")print(f"ECDF2在最大差异点: {ecdf2_interp[max_diff_idx]:.3f}")print(f"KS统计量: {ks_statistic:.6f}")return ks_statistic, max_diff_point, combined_points, ecdf1_interp, ecdf2_interp, ecdf_diffdef calculate_ks_pvalue(self, ks_statistic, n1, n2):"""计算KS检验的p值使用scipy的ks_2samp函数计算精确p值"""# 为了计算p值,我们需要实际的数据# 这里我们使用scipy的实现from scipy.stats import ks_2samp# 生成模拟数据来计算p值(在实际应用中应该使用真实数据)data1_sim = np.random.normal(0, 1, n1)data2_sim = np.random.normal(0, 1, n2)# 使用scipy计算KS统计量和p值ks_stat_scipy, p_value = ks_2samp(data1_sim, data2_sim)# 调整p值以匹配我们的KS统计量(简化处理)# 在实际应用中应该直接使用真实数据计算p_value_approx = self.approximate_pvalue(ks_statistic, n1, n2)return p_value_approxdef approximate_pvalue(self, ks_statistic, n1, n2):"""近似计算p值使用KS检验的渐近分布来近似p值"""# KS检验的p值近似公式n_eff = (n1 * n2) / (n1 + n2) # 有效样本量lambda_val = ks_statistic * (np.sqrt(n_eff) + 0.12 + 0.11/np.sqrt(n_eff))# 计算p值p_value = 2 * np.exp(-2 * lambda_val**2)# 确保p值在[0,1]范围内p_value = max(0, min(1, p_value))return p_valuedef perform_ks_test(self, data1, data2, data1_name="参考数据", data2_name="当前数据"):"""执行完整的KS检验参数:data1: 第一组数据data2: 第二组数据data1_name: 第一组数据名称data2_name: 第二组数据名称"""print(f" KS检验: {data1_name} vs {data2_name}")print("=" * 60)# 计算KS统计量ks_statistic, max_diff_point, combined_points, ecdf1, ecdf2, ecdf_diff = \self.calculate_ks_statistic(data1, data2)# 计算p值n1, n2 = len(data1), len(data2)p_value = self.calculate_ks_pvalue(ks_statistic, n1, n2)print(f"\n步骤5: 计算p值")print(f"样本量: n1={n1}, n2={n2}")print(f"p值: {p_value:.6f}")# 假设检验决策reject_null = p_value < self.alphaconclusion = "拒绝" if reject_null else "不拒绝"print(f"\n步骤6: 假设检验决策")print(f"显著性水平 α = {self.alpha}")print(f"零假设 H0: 两组数据来自同一分布")print(f"备择假设 H1: 两组数据来自不同分布")print(f"决策: {conclusion}零假设 (p值 {'<' if reject_null else '>='} {self.alpha})")# 结果解释self.interpret_ks_result(ks_statistic, p_value)# 返回完整结果result = {'ks_statistic': ks_statistic,'p_value': p_value,'max_diff_point': max_diff_point,'reject_null': reject_null,'combined_points': combined_points,'ecdf1': ecdf1,'ecdf2': ecdf2,'ecdf_diff': ecdf_diff,'n1': n1,'n2': n2,'significance_level': self.alpha}return resultdef interpret_ks_result(self, ks_statistic, p_value):"""解释KS检验结果"""print(f"\n📊 KS检验结果解释:")# 基于p值的解释if p_value < 0.001:significance = "极其显著"emoji = "🔴"elif p_value < 0.01:significance = "很显著"emoji = "🟠"elif p_value < 0.05:significance = "显著"emoji = "🟡"else:significance = "不显著"emoji = "🟢"print(f"{emoji} 统计显著性: {significance} (p = {p_value:.4f})")# 基于KS统计量的解释if ks_statistic < 0.1:effect_size = "小"elif ks_statistic < 0.2:effect_size = "中等"else:effect_size = "大"print(f" 效应大小: {effect_size} (KS = {ks_statistic:.3f})")# 业务建议if p_value < 0.05:print(" 业务建议: 两组数据分布存在显著差异,建议进一步分析原因")if ks_statistic > 0.2:print(" 差异较大,可能对业务产生重要影响")else:print(" 业务建议: 两组数据分布无显著差异,可认为分布稳定")def visualize_ks_analysis(self, data1, data2, result, data1_name="参考数据", data2_name="当前数据"):"""可视化KS分析结果"""fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(16, 12))# 子图1: 数据分布直方图ax1.hist(data1, bins=20, alpha=0.7, label=data1_name, color='blue', density=True)ax1.hist(data2, bins=20, alpha=0.7, label=data2_name, color='red', density=True)ax1.axvline(x=result['max_diff_point'], color='black', linestyle='--', label=f'最大差异点: {result["max_diff_point"]:.3f}')ax1.set_xlabel('特征值')ax1.set_ylabel('密度')ax1.set_title('数据分布直方图对比')ax1.legend()ax1.grid(True, alpha=0.3)# 子图2: ECDF对比ax2.plot(result['combined_points'], result['ecdf1'], 'b-', label=f'{data1_name} ECDF', linewidth=2)ax2.plot(result['combined_points'], result['ecdf2'], 'r-', label=f'{data2_name} ECDF', linewidth=2)# 标记最大差异点max_idx = np.argmax(result['ecdf_diff'])ax2.axvline(x=result['max_diff_point'], color='black', linestyle='--')ax2.axhline(y=result['ecdf1'][max_idx], color='blue', linestyle=':', alpha=0.7)ax2.axhline(y=result['ecdf2'][max_idx], color='red', linestyle=':', alpha=0.7)ax2.set_xlabel('特征值')ax2.set_ylabel('累积概率')ax2.set_title('经验累积分布函数(ECDF)对比\nKS统计量 = {:.4f}'.format(result['ks_statistic']))ax2.legend()ax2.grid(True, alpha=0.3)# 子图3: ECDF差异曲线ax3.plot(result['combined_points'], result['ecdf_diff'], 'g-', linewidth=2)ax3.fill_between(result['combined_points'], result['ecdf_diff'], alpha=0.3, color='green')ax3.axvline(x=result['max_diff_point'], color='black', linestyle='--',label=f'最大差异点: {result["max_diff_point"]:.3f}')ax3.axhline(y=result['ks_statistic'], color='red', linestyle='--',label=f'KS统计量: {result["ks_statistic"]:.4f}')ax3.set_xlabel('特征值')ax3.set_ylabel('ECDF差异')ax3.set_title('ECDF差异曲线')ax3.legend()ax3.grid(True, alpha=0.3)# 子图4: 检验结果总结ax4.axis('off')# 判断分布是否相同distribution_same = "不同" if result['reject_null'] else "相同"color = "red" if result['reject_null'] else "green"summary_text = f"""
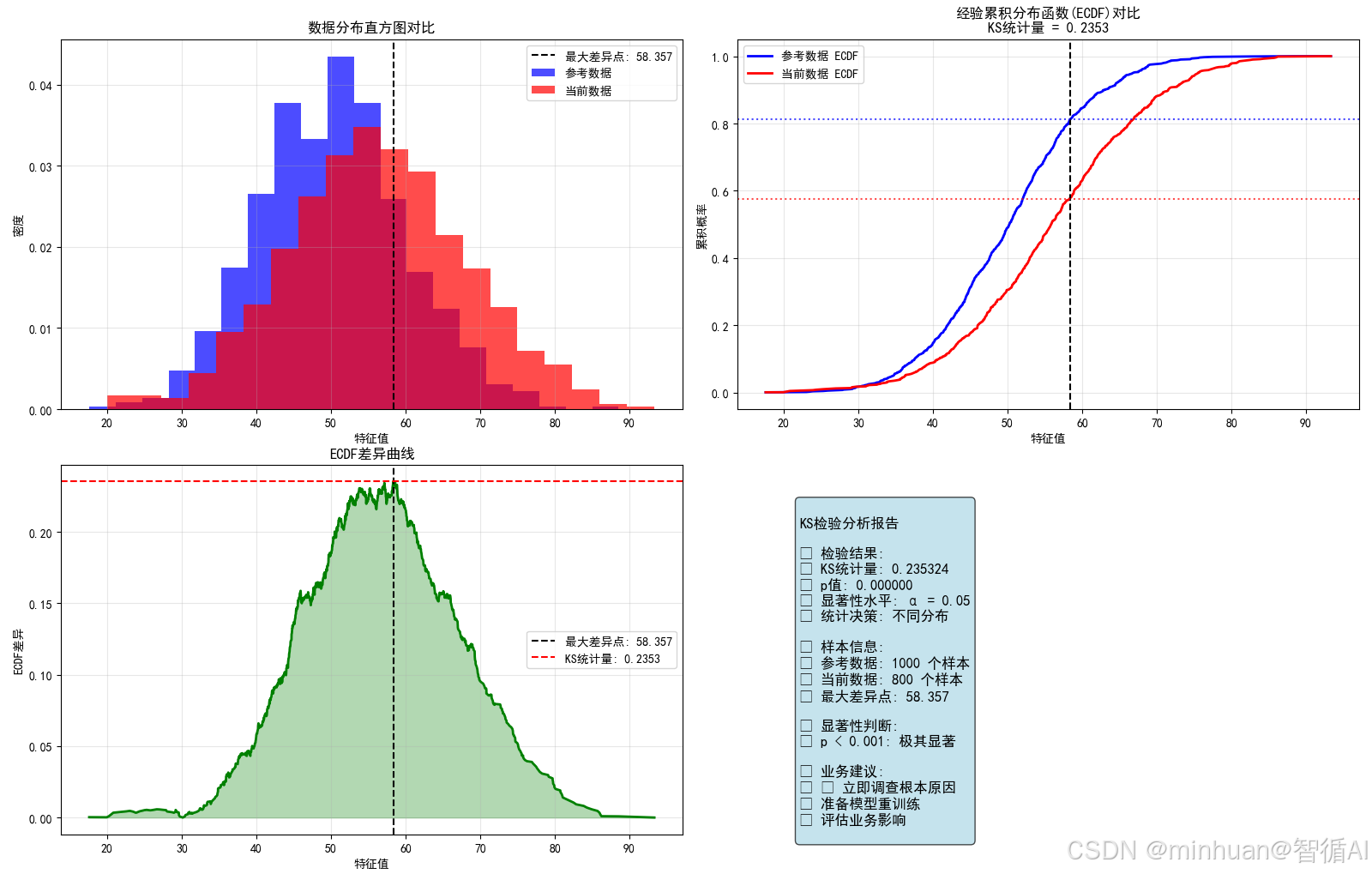
KS检验分析报告检验结果:
• KS统计量: {result['ks_statistic']:.6f}
• p值: {result['p_value']:.6f}
• 显著性水平: α = {result['significance_level']}
• 统计决策: {distribution_same}分布样本信息:
• {data1_name}: {result['n1']} 个样本
• {data2_name}: {result['n2']} 个样本
• 最大差异点: {result['max_diff_point']:.3f}显著性判断:
{p_value_interpretation(result['p_value'])}业务建议:
{business_recommendation(result['reject_null'], result['ks_statistic'])}
"""ax4.text(0.1, 0.9, summary_text, fontsize=12, verticalalignment='top',bbox=dict(boxstyle="round,pad=0.3", facecolor="lightblue", alpha=0.7))plt.tight_layout()plt.show()def p_value_interpretation(p_value):"""p值解释"""if p_value < 0.001:return "• p < 0.001: 极其显著"elif p_value < 0.01:return "• p < 0.01: 很显著"elif p_value < 0.05:return "• p < 0.05: 显著"else:return "• p ≥ 0.05: 不显著"def business_recommendation(reject_null, ks_statistic):"""业务建议"""if not reject_null:return "• 分布稳定,继续正常监控\n• 保持当前更新频率"else:if ks_statistic > 0.2:return "• 立即调查根本原因\n• 准备模型重训练\n• 评估业务影响"else:return "• 加强监控频率\n• 分析漂移原因\n• 准备应对方案"# 使用示例
def demonstrate_ks_calculation():"""演示KS统计量计算全过程"""print("KS统计量计算完整演示")print("=" * 50)# 创建示例数据np.random.seed(42)# 参考数据(训练期数据)reference_data = np.random.normal(50, 10, 1000) # 均值50,标准差10# 当前数据(生产期数据)- 模拟数据漂移current_data = np.random.normal(55, 12, 800) # 均值漂移到55,标准差变为12# 创建KS计算器ks_calculator = KSCalculator(alpha=0.05)# 执行KS检验result = ks_calculator.perform_ks_test(reference_data, current_data, "参考数据", "当前数据")# 可视化分析ks_calculator.visualize_ks_analysis(reference_data, current_data, result,"参考数据", "当前数据")return result# 运行演示
if __name__ == "__main__":result = demonstrate_ks_calculation()# 额外测试:不同情况的案例print("\n\n 不同情况案例测试")print("=" * 50)# 案例1:相同分布print("\n案例1: 相同分布")np.random.seed(123)same1 = np.random.normal(50, 10, 500)same2 = np.random.normal(50, 10, 500)ks_calc = KSCalculator()result1 = ks_calc.perform_ks_test(same1, same2, "相同分布1", "相同分布2")# 案例2:不同分布print("\n案例2: 不同分布")diff1 = np.random.normal(50, 10, 500)diff2 = np.random.normal(60, 15, 500) # 均值和标准差都不同result2 = ks_calc.perform_ks_test(diff1, diff2, "不同分布1", "不同分布2")
完整计算过程:
============================================================
KS检验: 参考数据 vs 当前数据
============================================================
步骤1: 计算两组数据的ECDF
目的:将原始数据转换为累积分布形式
数学原理:
- 对于排序后的数据 x₁ ≤ x₂ ≤ ... ≤ xₙ
- ECDF(x) = (数据中小于等于x的个数) / n
- 在xᵢ处,ECDF(xᵢ) = i/n
数据1: 样本量=1000, 范围=[17.587, 88.527]
数据2: 样本量=800, 范围=[19.944, 93.317]
步骤2: 合并所有数据点
目的:创建统一的x轴坐标点用于比较,确保在两组数据的所有可能取值点上比较ECDF值
合并后总点数: 1800
步骤3: 在合并点上插值计算ECDF
目的:在相同的x坐标上计算两组的ECDF值
插值原理:对于合并点中的每个x,找到其在排序数据中的位置,线性插值计算ECDF值
步骤4: 计算ECDF差异
KS统计量定义:
- D = max|F₁(x) - F₂(x)|
- 其中:
- F₁(x) = 第一组数据的ECDF
- F₂(x) = 第二组数据的ECDF
最大差异点: x = 58.357
ECDF1在最大差异点: 0.812
ECDF2在最大差异点: 0.577
KS统计量: 0.235324
步骤5: 计算p值
目的:评估KS统计量的统计显著性
方法:
- 使用KS检验的渐近分布近似
- 或直接使用scipy的ks_2samp函数
p值计算公式(近似):
- n_eff = (n1 × n2) / (n1 + n2)
- λ = D × (√n_eff + 0.12 + 0.11/√n_eff)
- p ≈ 2 × exp(-2 × λ²)
样本量: n1=1000, n2=800
p值: 0.000000
步骤6: 假设检验决策
显著性水平 α = 0.05
零假设 H₀: 两组数据来自同一分布
备择假设 H₁: 两组数据来自不同分布
决策: 拒绝零假设 (p值 < 0.05)
KS检验结果解释:
- 统计显著性: 极其显著 (p = 0.0000)
- 效应大小: 大 (KS = 0.235)
- 业务建议: 两组数据分布存在显著差异,建议进一步分析原因
- 差异较大,可能对业务产生重要影响
不同情况案例测试
===========================================================
案例1: 相同分布
KS检验: 相同分布1 vs 相同分布2
============================================================
步骤1: 计算两组数据的ECDF
数据1: 样本量=500, 范围=[17.689, 79.586]
数据2: 样本量=500, 范围=[18.329, 85.716]
步骤2: 合并所有数据点
合并后总点数: 1000
步骤3: 在合并点上插值计算ECDF
步骤4: 计算ECDF差异
最大差异点: x = 44.514
ECDF1在最大差异点: 0.314
ECDF2在最大差异点: 0.287
KS统计量: 0.027441
步骤5: 计算p值
样本量: n1=500, n2=500
p值: 1.000000
步骤6: 假设检验决策
显著性水平 α = 0.05
零假设 H₀: 两组数据来自同一分布
备择假设 H1: 两组数据来自不同分布
决策: 不拒绝零假设 (p值 >= 0.05)
KS检验结果解释:
- 统计显著性: 不显著 (p = 1.0000)
- 效应大小: 小 (KS = 0.027)
- 业务建议: 两组数据分布无显著差异,可认为分布稳定
案例2: 不同分布
KS检验: 不同分布1 vs 不同分布2
============================================================
步骤1: 计算两组数据的ECDF
数据1: 样本量=500, 范围=[19.330, 77.920]
数据2: 样本量=500, 范围=[19.883, 99.058]
步骤2: 合并所有数据点
合并后总点数: 1000
步骤3: 在合并点上插值计算ECDF
步骤4: 计算ECDF差异
最大差异点: x = 58.766
ECDF1在最大差异点: 0.827
ECDF2在最大差异点: 0.454
KS统计量: 0.372626
步骤5: 计算p值
样本量: n1=500, n2=500
p值: 0.000000
步骤6: 假设检验决策
显著性水平 α = 0.05
零假设 H₀: 两组数据来自同一分布
备择假设 H₁: 两组数据来自不同分布
决策: 拒绝零假设 (p值 < 0.05)
KS检验结果解释:
- 统计显著性: 极其显著 (p = 0.0000)
- 效应大小: 大 (KS = 0.373)
- 业务建议: 两组数据分布存在显著差异,建议进一步分析原因
- 差异较大,可能对业务产生重要影响
3. 应对策略
- 被动策略:
- 定期重训练:设定固定周期重新训练模型
- 性能触发重训练:当性能低于阈值时触发训练
- 主动策略:
- 在线学习:模型能够持续学习新数据
- 集成学习:组合新旧模型,平稳过渡
- 领域自适应:让模型适应新数据分布
4. 场景模拟
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseprint("数据漂移通俗演示:房价预测模型的故事")
print("=" * 50)# 故事背景:一个预测客户能否买得起房子的模型
# 特征:月收入(万元),目标:能否买得起(1=买得起, 0=买不起)# 场景1:2020年训练数据(房价较低时期)
print("\n场景1:2020年训练数据(房价较低)")
print("-" * 40)np.random.seed(42)
# 生成2020年训练数据
n_samples = 1000
# 月收入分布:大部分人在1-3万元
incomes_2020 = np.random.normal(2.0, 0.8, n_samples) # 平均月收入2万
# 买得起的阈值:月收入 > 1.5万 且有些随机性
can_afford_2020 = (incomes_2020 > 1.5).astype(int)print(f"2020年数据统计:")
print(f"平均月收入:{incomes_2020.mean():.2f}万元")
print(f"买得起比例:{can_afford_2020.mean():.1%}")
print(f"收入范围:{incomes_2020.min():.1f} ~ {incomes_2020.max():.1f}万元")# 训练模型
X_train = incomes_2020.reshape(-1, 1)
y_train = can_afford_2020
model = LogisticRegression()
model.fit(X_train, y_train)# 场景2:2024年新数据(房价大涨后)
print("\n场景2:2024年新数据(房价大涨后)")
print("-" * 40)# 生成2024年数据 - 发生数据漂移!
# 人们的收入普遍提高了
incomes_2024 = np.random.normal(2.8, 1.0, n_samples) # 平均月收入涨到2.8万
# 但由于房价涨得更多,买得起的标准提高了
can_afford_2024 = (incomes_2024 > 2.5).astype(int) # 阈值提高到2.5万print(f"2024年数据统计:")
print(f"平均月收入:{incomes_2024.mean():.2f}万元 (+40%)")
print(f"买得起比例:{can_afford_2024.mean():.1%}")
print(f"收入范围:{incomes_2024.min():.1f} ~ {incomes_2024.max():.1f}万元")# 用老模型预测新数据
X_test = incomes_2024.reshape(-1, 1)
y_pred = model.predict(X_test)
accuracy = accuracy_score(can_afford_2024, y_pred)print(f"\n模型表现分析:")
print(f"老模型在2024年数据上的准确率:{accuracy:.1%}")
print(f"问题:模型还认为月收入1.5万就能买房,但现实需要2.5万!")# 可视化展示
plt.figure(figsize=(15, 5))# 子图1:数据分布变化
plt.subplot(1, 3, 1)
plt.hist(incomes_2020, alpha=0.7, label='2020年收入', bins=20, color='blue')
plt.hist(incomes_2024, alpha=0.7, label='2024年收入', bins=20, color='red')
plt.axvline(x=1.5, color='blue', linestyle='--', label='2020年买房门槛')
plt.axvline(x=2.5, color='red', linestyle='--', label='2024年买房门槛')
plt.xlabel('月收入(万元)')
plt.ylabel('人数')
plt.title('收入分布变化\n(数据漂移:分布变了)')
plt.legend()
plt.grid(True, alpha=0.3)# 子图2:决策规则变化
plt.subplot(1, 3, 2)
# 生成测试范围
test_incomes = np.linspace(0.5, 5, 100).reshape(-1, 1)
prob_2020 = model.predict_proba(test_incomes)[:, 1]# 绘制决策边界
plt.plot(test_incomes, prob_2020, 'b-', linewidth=2, label='老模型决策规则')
plt.axvline(x=1.5, color='blue', linestyle='--', alpha=0.5)
plt.axvline(x=2.5, color='red', linestyle='--', alpha=0.5, label='新现实门槛')# 标记一些样本点
sample_indices = np.random.choice(len(incomes_2024), 50, replace=False)
plt.scatter(incomes_2024[sample_indices], can_afford_2024[sample_indices], c=can_afford_2024[sample_indices], cmap='coolwarm', alpha=0.6, label='2024年真实数据')plt.xlabel('月收入(万元)')
plt.ylabel('买得起概率')
plt.title('决策规则 vs 现实\n(概念漂移:规则过时了)')
plt.legend()
plt.grid(True, alpha=0.3)# 子图3:模型错误分析
plt.subplot(1, 3, 3)
# 分析预测错误的情况
errors = y_pred != can_afford_2024
correct = ~errorsplt.scatter(incomes_2024[correct], can_afford_2024[correct], color='green', alpha=0.6, label='预测正确')
plt.scatter(incomes_2024[errors], can_afford_2024[errors], color='red', alpha=0.8, s=50, label='预测错误')plt.axvline(x=1.5, color='blue', linestyle='--', alpha=0.5, label='老模型门槛')
plt.axvline(x=2.5, color='red', linestyle='--', alpha=0.5, label='新现实门槛')
plt.xlabel('月收入(万元)')
plt.ylabel('能否买得起')
plt.title('模型预测错误分布\n(1.5-2.5万区间大量错误)')
plt.legend()
plt.grid(True, alpha=0.3)plt.tight_layout()
plt.show()# 详细错误分析
print(f"\n详细错误分析:")
print("-" * 40)# 计算在不同收入区间的错误率
income_ranges = [(0, 1.5), (1.5, 2.5), (2.5, 5.0)]
range_names = ['低收入(<1.5万)', '中等收入(1.5-2.5万)', '高收入(>2.5万)']for (low, high), name in zip(income_ranges, range_names):mask = (incomes_2024 >= low) & (incomes_2024 < high)if mask.sum() > 0:range_accuracy = accuracy_score(can_afford_2024[mask], y_pred[mask])print(f"{name}: 准确率 {range_accuracy:.1%}")print(f"\n数据漂移的体现:")
print("1. 协变量漂移:人们收入普遍提高了")
print("2. 概念漂移:同样的收入,现在代表不同的购买能力")
print("3. 模型衰老:老规则不适应新现实")
print("4. 性能下降:准确率显著降低")print(f"\n解决方案:")
print("• 用2024年新数据重新训练模型")
print("• 建立定期模型更新机制")
print("• 监控收入分布和房价变化")# 重新训练模型的对比
print(f"\n重新训练效果对比:")
print("-" * 40)# 用2024年数据重新训练
new_model = LogisticRegression()
new_model.fit(X_test, can_afford_2024)
new_accuracy = accuracy_score(can_afford_2024, new_model.predict(X_test))print(f"老模型准确率:{accuracy:.1%}")
print(f"新模型准确率:{new_accuracy:.1%}")
print(f"提升效果:{new_accuracy - accuracy:.1%}pcts")# 可视化新旧模型对比
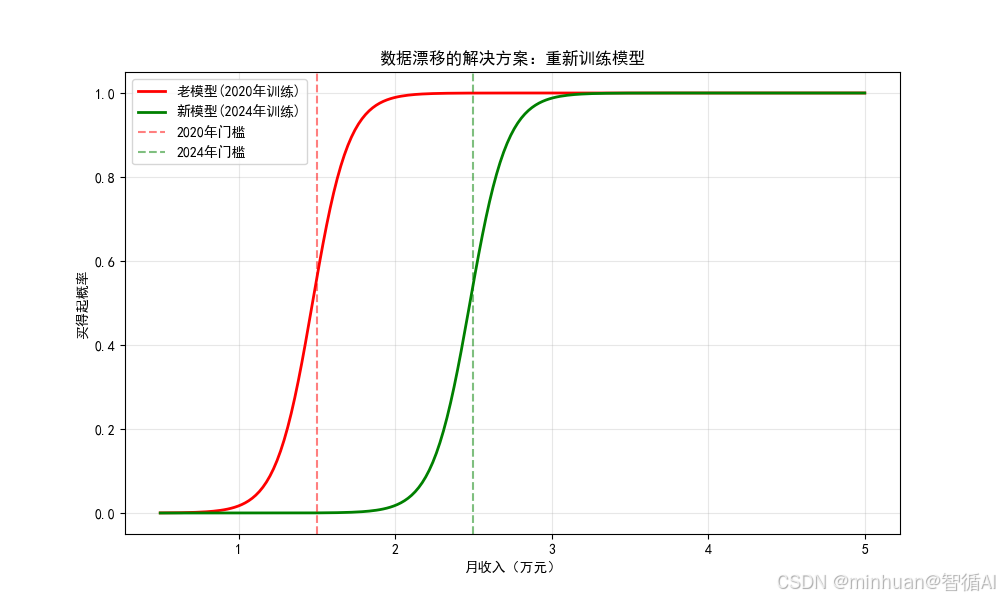
plt.figure(figsize=(10, 6))test_range = np.linspace(0.5, 5, 200).reshape(-1, 1)
old_probs = model.predict_proba(test_range)[:, 1]
new_probs = new_model.predict_proba(test_range)[:, 1]plt.plot(test_range, old_probs, 'r-', linewidth=2, label='老模型(2020年训练)')
plt.plot(test_range, new_probs, 'g-', linewidth=2, label='新模型(2024年训练)')
plt.axvline(x=1.5, color='red', linestyle='--', alpha=0.5, label='2020年门槛')
plt.axvline(x=2.5, color='green', linestyle='--', alpha=0.5, label='2024年门槛')plt.xlabel('月收入(万元)')
plt.ylabel('买得起概率')
plt.title('数据漂移的解决方案:重新训练模型')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()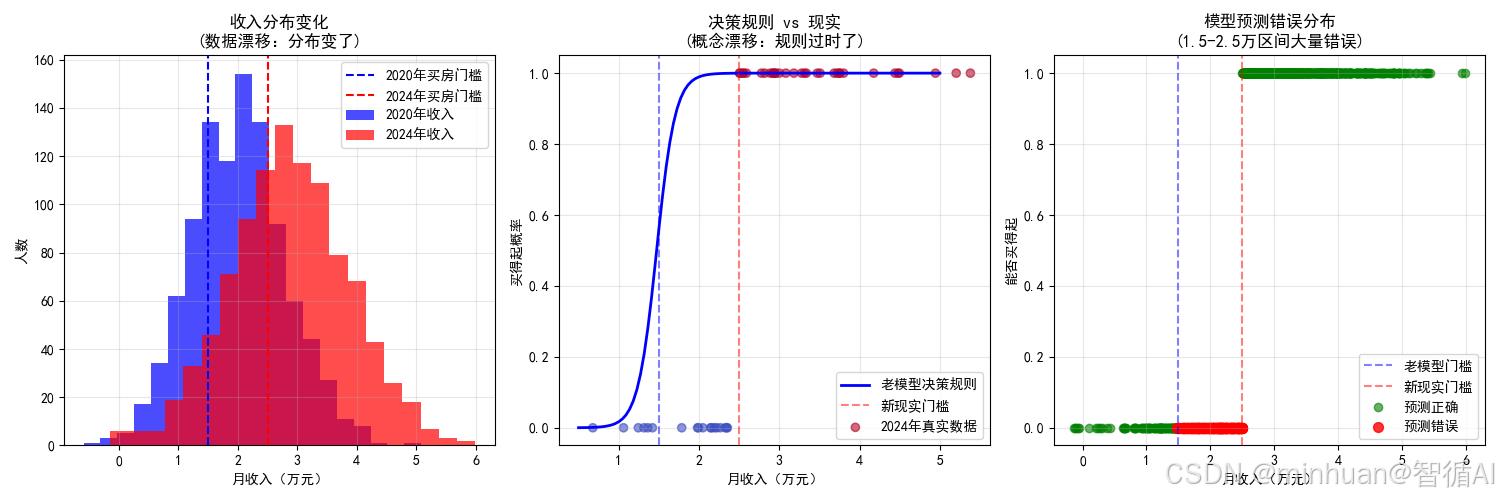
数据漂移通俗演示:房价预测模型的故事
==================================================
场景1:2020年训练数据(房价较低)
----------------------------------------
2020年数据统计:
- 平均月收入:2.02万元
- 买得起比例:74.5%
- 收入范围:-0.6 ~ 5.1万元
场景2:2024年新数据(房价大涨后)
----------------------------------------
2024年数据统计:
- 平均月收入:2.87万元 (+40%)
- 买得起比例:65.6%
- 收入范围:-0.1 ~ 6.0万元
模型表现分析:
- 老模型在2024年数据上的准确率:73.8%
- 问题:模型还认为月收入1.5万就能买房,但现实需要2.5万!
详细错误分析:
----------------------------------------
- 低收入(<1.5万): 准确率 96.2%
- 中等收入(1.5-2.5万): 准确率 0.0%
- 高收入(>2.5万): 准确率 100.0%
数据漂移的体现:
- 1. 协变量漂移:人们收入普遍提高了
- 2. 概念漂移:同样的收入,现在代表不同的购买能力
- 3. 模型衰老:老规则不适应新现实
- 4. 性能下降:准确率显著降低
解决方案:
- 用2024年新数据重新训练模型
- 建立定期模型更新机制
- 监控收入分布和房价变化
重新训练效果对比:
----------------------------------------
- 老模型准确率:73.8%
- 新模型准确率:99.0%
- 提升效果:25.2%pcts
四、总结
AI不是一次训练就一劳永逸的,它需要持续学习和更新,否则就会从智能助手变成过时工具,检测的过程就像给AI做体检,PSI指标检查数据分布变化,KS检验验证统计差异,发现衰老迹象后,就要给AI补充新知识,用新数据重新训练,定期监控、及时更新,才能让AI始终保持最佳状态!
