平衡二叉树-力扣

核心思路总结

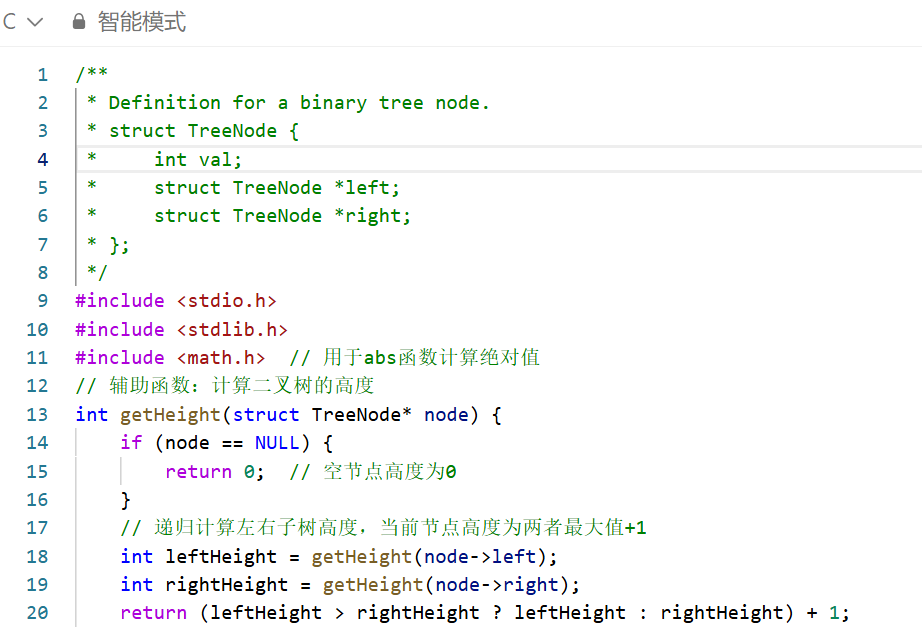
判断二叉树是否为平衡二叉树的核心思路基于平衡二叉树的定义：二叉树中每个节点的左右两个子树的高度差的绝对值不超过 1。具体实现逻辑如下：

对每个节点，递归计算其左、右子树的高度。

检查当前节点的左、右子树高度差是否超过 1，若超过则不是平衡二叉树。

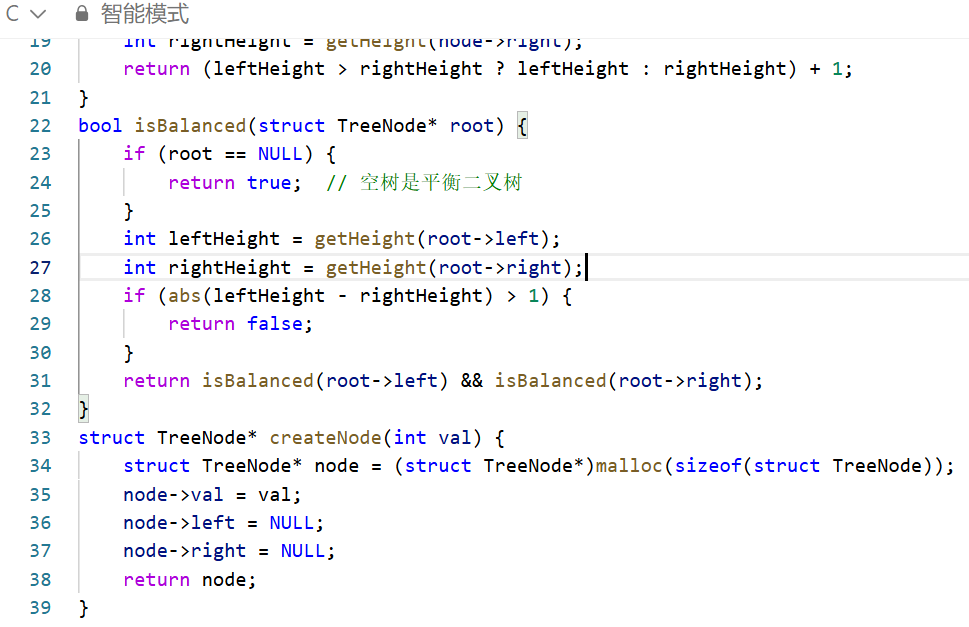
递归检查当前节点的左子树和右子树是否也满足上述条件（即子树本身也是平衡二叉树）。

空树默认是平衡二叉树（递归终止条件）。

原理总结

高度计算原理：通过递归遍历二叉树，空节点高度为 0，非空节点的高度 = 左右子树高度的最大值 + 1（自身节点占一层）。

平衡判断原理：对每个节点，先判断自身的左右子树高度差是否合法（≤1），再递归判断左、右子树是否整体平衡。只有所有节点都满足条件，整个树才是平衡二叉树。

递归逻辑：利用二叉树的递归结构，将 “判断整棵树是否平衡” 拆解为 “判断根节点是否平衡”+“判断左子树是否平衡”+“判断右子树是否平衡”，逐层深入直到叶子节点。

优点总结

思路直观易懂：完全贴合平衡二叉树的定义，逻辑直接，初学者容易理解和实现。

实现简单：仅需两个核心函数（计算高度、判断平衡），代码量少，结构清晰。

正确性有保障：通过递归覆盖所有节点，确保每个节点的平衡条件都被检查，不存在遗漏。

适用性广：对任意二叉树（包括空树、单节点树、完全二叉树等）均有效，无特殊限制。