当前位置： 首页 > news >正文

TensorFlow 2.x常用函数总结（持续更新）

news 2025/11/4 8:53:30

本文主要记录自己在用 Tensorflow 2.x 复现经典模型过程中遇到的一些函数及用法，方便查阅

目录

tf 2.x 常用函数

tf.zeros_like()

tf.ones() / tf.ones_like()

tf.cast()

tf.equal() / tf.not_equal()

tf.logical_or() / tf.logical_and() / tf.logical_not()

tf.greater() / tf.less()

tf.sign()

tf.clip_by_value()

tf.identity()

tf.fill()

tf.size()

tf.squeeze() / tf.unsqueeze()

tf.where()

tf.cond()

tf.concat()

tf.stack()

tf.reduce_mean() / tf.reduce_sum() / tf.reduce_max()

tf.reduce_all() / tf.reduce_any()

tf.tile()

tf.boolean_mask()

tf.gather() / tf.gather_nd()

tf.scatter_nd()

tf.slice()

tf.multiply() / *

tf.matmul() / @

tf.transpose()

tf.add_n()

tf.divide()

tf.maximum() / tf.reduce_max()

tf.math.subtract()

tf.pow() / tf.exp() / tf.abs()

tf.math.rint()

tf.math.log1p()

tf.nn.l2_normalize()

tf.nn.relu()

tf.random.normal()

tf.expand_dims()

tf.reshape()

tf.range()

tf.sequence_mask()

tf.nn.embedding_lookup()

其他常用

class、__init__、call

assign_sub / assign

tf.float32.min

logging.info()

tf 2.x 常用函数

tf.zeros_like()

用于生成一个和输入张量（tensor）具有相同形状和数据类型、但所有元素都是零的新张量

import tensorflow as tf# 创建一个张量
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])# 使用 tf.zeros_like() 创建一个和上面张量相同形状和数据类型的全零张量
zero_tensor = tf.zeros_like(tensor)
print(zero_tensor)

输出结果为：

tf.Tensor(
[[0 0 0][0 0 0]], shape=(2, 3), dtype=int32)

同理，若创建全1张量，函数为tf.ones_like()

tf.ones() / tf.ones_like()

它们的主要作用都是生成元素全为1的张量，但存在一些区别：

  • tf.ones()需要一个形状为参数，然后返回一个与给定形状相匹配的、全是1的新张量
  • tf.ones_like()需要一个已存在的张量作为参数，然后返回一个与给定张量形状相同的、全是1的新张量，无需手动指定形状
import tensorflow as tfa = tf.ones((2, 3))    # 输出一个形状为(2,3)、元素全为1的张量
print(a)# 输出一个与tensor形状相同、元素全为1的新张量
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
b = tf.ones_like(tensor)
print(b)

总的来说，tf.ones() 需要手动指定形状，而 tf.ones_like() 则是根据已存在的张量的形状来创建新的元素全为1的张量

tf.cast()

用来改变Tensor的数据类型。如果在转换过程中，原Tensor的数值无法适应新的数据类型，则会产生一定形式的截断

  • 输入：待转换的Tensor以及目标数据类型
  • 输出：一个新的数据类型转换后的Tensor
import tensorflow as tf# 创建一个float类型的Tensor
x = tf.constant([1.8, 2.2], dtype=tf.float32)# 使用cast函数将其转换为int32类型的Tensor
x_cast = tf.cast(x, tf.int32)
print(x_cast)

输出结果为：

tf.Tensor([1 2], shape=(2,), dtype=int32)

可以看到，小数部分被截断，只保留整数部分，这就是tf.cast函数的数据类型转换功能

tf.equal() / tf.not_equal()

tf.equal()函数是用来比较两个具有相同维度和形状的tensor中的对应元素是否相等。会逐元素地进行比较，如果对应位置的元素相等返回True，否则返回False

import tensorflow as tf# 创建两个tensor
tensor1 = tf.constant([1, 2, 3, 4])
tensor2 = tf.constant([1, 2, 3, 5])# 返回一个布尔型张量，其中每个元素代表了相应位置的元素是否相等
equal_comparison = tf.equal(tensor1, tensor2)
print(equal_comparison)

输出结果为：

tf.Tensor([ True  True  True False], shape=(4,), dtype=bool)

tf.not_equal()函数则相反，用于判断两个张量中的元素是否不相等。若对应位置元素不相等返回True，否则返回False

import tensorflow as tf# 创建两个tensor
tensor1 = tf.constant([1, 2, 3, 4])
tensor2 = tf.constant([2, 2, 3, 3])equal_comparison = tf.not_equal(tensor1, tensor2)
print(equal_comparison)

输出结果为：

tf.Tensor([ True  False  False True], shape=(4,), dtype=bool)

tf.logical_or() / tf.logical_and() / tf.logical_not()

tf.logical_or()用于执行元素级的逻辑或运算（只要有一个True就返回True）

  • 输入：两个布尔类型的张量
  • 输出：一个布尔类型张量，每一个元素都是对应位置上的两个元素的逻辑或结果
import tensorflow as tf# 创建两个布尔型张量
tensor1 = tf.constant([True, False, True, False])
tensor2 = tf.constant([False, False, True, True])result = tf.logical_or(tensor1, tensor2)
print(result)

输出结果为：

tf.Tensor([ True False  True  True], shape=(4,), dtype=bool)

tf.logical_and() 和 tf.logical_not() 同理，分别是逻辑与（全为True才返回True）、逻辑非（取反）运算

  • 逻辑与 tf.logical_and()
import tensorflow as tf# 创建两个布尔型张量
tensor1 = tf.constant([True, False, True, False])
tensor2 = tf.constant([True, True, False, False])result = tf.logical_and(tensor1, tensor2)
print(result)

输出结果为：

tf.Tensor([ True False  False  False], shape=(4,), dtype=bool)
  • 逻辑非 tf.logical_not()：输入是一个或多个布尔值的张量，输出是一个同维度的布尔张量
import tensorflow as tf# 创建一个布尔型的张量
bool_tensor = tf.constant([True, False, True, False])tensor = tf.logical_not(bool_tensor)
print(tensor)

输出结果为：

tf.Tensor([False  True False  True], shape=(4,), dtype=bool)

tf.greater() / tf.less()

tf.greater()用于执行元素级别的大于比较

  • 输入：两个需要比较大小的tensor
  • 输出：一个与输入相同形状的新的布尔型tensor。其中每一个元素表示在对应位置上，第一个tensor中的元素是否大于第二个tensor中的元素，大于则为True，否则为False
import tensorflow as tfa = tf.constant([1, 2, 3])
b = tf.constant([2, 2, 2])result = tf.greater(a, b)
print(result)

输出结果为：

tf.Tensor([False False True], shape=(3,), dtype=bool)

tf.less()同理，进行元素级别的小于比较

import tensorflow as tfa = tf.constant([1, 2, 3])
b = tf.constant([2, 2, 2])result = tf.less(a, b)
print(result)

输出结果为：

tf.Tensor([True False False], shape=(3,), dtype=bool)

tf.sign()

tf.sign()将输入张量中的正数转换为1，负数转换为-1，而 0 则保持不变。返回的张量与输入的张量形状相同

import tensorflow as tfx = tf.constant([1.8, -2.2, 0, -3.3, 2.5], dtype=tf.float32)x_sign = tf.sign(x)
print(x_sign)

输出结果为：

tf.Tensor([ 1. -1.  0. -1.  1.], shape=(5,), dtype=float32)

tf.clip_by_value()

tf.clip_by_value()用于将张量中的数值限制在某个范围内。这个函数的标准使用方法如下：

tf.clip_by_value(t, clip_value_min, clip_value_max)

在这里，t是待截取的张量，clip_value_min 和 clip_value_max 则分别是待截取范围的最小值和最大值。函数返回一个新的、按指定的最小值和最大值截取的张量

import tensorflow as tft = tf.constant([0.9, 2.5, 3.3, 4.5])clip_t = tf.clip_by_value(t, 1.0, 3.0)
print(clip_t)

输出结果为：

tf.Tensor([1.  2.5 3.  3. ], shape=(4,), dtype=float32)

tf.clip_by_value()在训练深度学习模型时非常实用。例如在训练神经网络时，可以用这个函数来防止梯度消失或爆炸，使学习率保持在一个合理的范围内

tf.identity()

tf.identity()用于创建一个与输入tensor相同的新tensor（独立于输入tensor）

import tensorflow as tfx = tf.constant([2, 3, 4])
y = tf.identity(x)    # y被定义为x的副本，但独立于x，即对y的操作不会影响xprint("x: ", x)
print("y: ", y)

输出结果为：

x:  tf.Tensor([2 3 4], shape=(3,), dtype=int32)
y:  tf.Tensor([2 3 4], shape=(3,), dtype=int32)

一个使用 tf.identity()的常见场景是为 tensor 添加一个名称（可以帮助我们在复杂的神经网络中更好地追踪和调试tensor），如：

x = tf.constant([2, 3, 4])y = tf.identity(x, name="my_tensor")
print("y: ", y)    # 输出结果同上

tf.fill()

tf.fill()作用是创建一个指定维度和数值的张量

tf.fill(dims, value)

其中 dims 是一个列表，代表了想要创建的张量的形状；value 是想要填充的值

import tensorflow as tf# 创建一个形状为[2,3]，所有元素值为9的张量
a = tf.fill([2, 3], 9)
print(a)

输出结果为：

tf.Tensor(
[[9 9 9][9 9 9]], shape=(2, 3), dtype=int32)

tf.size()

tf.size()函数返回的是一个Scalar Tensor，即一个单一数值，表示输入Tensor 包含的元素个数，为所有维度大小的乘积

import tensorflow as tfa = tf.constant([[1, 2, 3], [4, 5, 6]])   # 形状是(2,3)
print(tf.size(a))   # 返回 6 = 2 * 3

输出结果为：

tf.Tensor(6, shape=(), dtype=int32)

tf.squeeze() / tf.unsqueeze()

tf.squeeze()作用是从张量中移除所有长度为1的维度。例如，如果有一个形状为 [1, 3, 1, 4, 1] 的张量，使用 tf.squeeze()函数后，会得到一个形状为 [3, 4] 的张量

需要注意的是，tf.squeeze()函数默认会移除所有长度为1的维度。如果只想移除特定的长度为1的维度，可以通过 axis 参数指定。例如，tf.squeeze(tensor, axis=[2, 4]) 只会移除第2和第4维（从0开始计数）

import tensorflow as tf# 创建一个形状为 [1, 3, 1, 4, 1] 的张量
tensor = tf.ones([1, 3, 1, 4, 1])# 使用 tf.squeeze 并指定axis 移除特定的长度为1的维度
squeezed_tensor = tf.squeeze(tensor, axis=[2, 4])
print(squeezed_tensor.shape)

输出结果为：

(1, 3, 4)

注：逆操作为 tf.unsqueeze()

tf.where()

tf.where()函数主要用于根据条件选择元素或获取张量中非零元素的索引

（1）根据条件选择元素：tf.where(condition, x, y)

  • 根据 condition 从 x 和 y 中选择元素，当 condition 为 True 时，选择 x 中对应位置的元素；当 condition 为 False 时，选择 y 中对应位置的元素
  • 返回 tensor 与 condition 的 shape 是相同的
  • 支持广播，当 x 和 y 的形状与 condition 不匹配时会自动广播
import tensorflow as tfcondition = tf.constant([[True, False], [False, True]])
x = tf.constant([[1, 2], [3, 4]])
y = tf.constant([[10, 20], [30, 40]])result = tf.where(condition, x, y)
print(result.numpy())

输出结果为：

[[ 1 20][30  4]]

（2）获取非零元素的索引：tf.where(condition)

  • 返回 condition 中为 True 的元素的索引，返回张量的形状为 [num_true, rank]

import tensorflow as tf# 一维示例
tensor = tf.constant([0, 5, 0, 8, 0, 3])
indices = tf.where(tensor)
print(indices.numpy())# 二维示例
matrix = tf.constant([[0, 1, 0],[1, 0, 1],[0, 0, 1]])
indices_2d = tf.where(matrix)
print(indices_2d.numpy())

输出结果为：

[[1][3][5]][[0 1][1 0][1 2][2 2]]

对比 tf.where() 和 tf.boolean_mask()：

# 相同的数据过滤，boolean_mask vs where 两种方法对比
tensor = tf.constant([1, 2, 3, 4, 5])
mask = tf.constant([True, False, True, False, True])# 使用 boolean_mask
result_mask = tf.boolean_mask(tensor, mask)
print("boolean_mask 结果:", result_mask.numpy())  # [1 3 5]# 使用 where 实现相同功能
indices = tf.where(mask)
print(indices)
# tf.Tensor([[0]
#            [2]
#            [4]], shape=(3, 1), dtype=int64)print(indices[:, 0])   # tf.Tensor([0 2 4], shape=(3,), dtype=int64)result_where = tf.gather(tensor, indices[:, 0])
print("where+gather 结果:", result_where.numpy())  # [1 3 5]

tf.cond()

用于条件执行的控制流函数，根据条件选择执行两个不同计算分支中的一个

tf.cond(pred, true_fn, false_fn, name=None)
  • pred：标量布尔张量，决定执行哪个分支，且两个分支必须返回相同的数据类型和形状
  • true_fn：可调用函数，当 pred 为 True 时执行
  • false_fn：可调用函数，当 pred 为 False 时执行
# 如果 x 等于 y，则操作返回 x + z 的值，否则返回 y 的平方值
result = tf.cond(tf.equal(x, y), lambda: tf.add(x, z), lambda: tf.square(y))

应用：梯度裁剪（Gradient Clipping。作用是防止梯度爆炸，通过限制梯度大小来稳定训练过程）

import tensorflow as tf# 根据梯度大小决定是否进行梯度裁剪
gradients = tf.constant([1.5, -2.3, 0.8, 4.1])
max_grad_norm = 2.0   # 最大梯度范数阈值# 计算梯度的L2范数（欧几里得范数）
grad_norm = tf.sqrt(tf.reduce_sum(tf.square(gradients)))
# 等价于：||gradients||₂ = √(Σ gradientᵢ²)def clip_fn():# 需要裁剪的情况scale = max_grad_norm / grad_norm   # 缩放比例return gradients * scale   # 按比例缩放梯度def no_clip_fn():# 不需要裁剪的情况return gradientsclipped_gradients = tf.cond(grad_norm > max_grad_norm, clip_fn, no_clip_fn)

与 tf.where() 相比，tf.cond() 真正控制计算图的执行路径，而 tf.where() 会计算所有分支然后选择结果。这使得 tf.cond() 在需要避免不必要计算时更加高效

tf.concat()

tf.concat()函数用于将两个或更多的张量沿特定的轴连接（拼接）在一起，前提条件是拼接的张量具有相同的数据类型，且在非连接轴上的维度必须相同

tf.concat(values, axis, name=None)
  • values：要连接的张量列表或元组
  • axis：axis=0（行）为纵向拼接，axis=1（列）为横向拼接。默认axis=0
  • name：操作的名称（可选）
import tensorflow as tf### 一维示例 ###
t1 = tf.constant([1, 2, 3])
t2 = tf.constant([4, 5, 6])# 沿着第0维连接（默认）
result0 = tf.concat([t1, t2], axis=0)
print(result0.numpy())  # 输出: [1 2 3 4 5 6]### 二维示例 ###
a = tf.constant([[1, 2, 3],[4, 5, 6]])
b = tf.constant([[7, 8, 9],[10, 11, 12]])# 沿着第0维连接（垂直堆叠）
result_0 = tf.concat([a, b], axis=0)
print(result_0.numpy())
# 输出:
# [[ 1  2  3]
#  [ 4  5  6]
#  [ 7  8  9]
#  [10 11 12]]# 沿着第1维连接（水平堆叠）
result_1 = tf.concat([a, b], axis=1)
print(result_1.numpy())
# 输出:
# [[ 1  2  3  7  8  9]
#  [ 4  5  6 10 11 12]]

三维及以上张量拼接的维度变化：如两个 shape 为 (2, 2, 2) 的三维张量做连接。若axis=0，则输出 shape 为 (4, 2, 2)；若axis=1，则输出 shape 为 (2, 4, 2)；若axis=2，则输出 shape 为 (2, 2, 4)

与tf.stack()函数的区别：

import tensorflow as tfa = tf.constant([1, 2, 3])
b = tf.constant([4, 5, 6])concat_result = tf.concat([a, b], axis=0)  # 形状: (6,)
stack_result = tf.stack([a, b], axis=0)    # 形状: (2, 3)print("concat 结果: \n", concat_result)
print("stack 结果: \n", stack_result)

输出结果为：

concat 结果: tf.Tensor([1 2 3 4 5 6], shape=(6,), dtype=int32)stack 结果: tf.Tensor(
[[1 2 3][4 5 6]], shape=(2, 3), dtype=int32)

tf.stack()

tf.stack()是一个用于将多个张量沿新维度堆叠的操作。它的功能类似于numpy中的np.stack()，能够将一组相同形状的张量合并为一个更高维的张量

tf.stack(values, axis=0, name='stack')
  • 参数：
    • values：一个张量列表（所有张量必须有相同的形状和数据类型）
    • axis：指定堆叠的维度（默认为0，即第一个维度）
    • name：操作的名称（可选）
  • 返回：堆叠后的新张量，比输入张量多一个维度
import tensorflow as tf# 定义两个形状相同的张量
x = tf.constant([1, 2, 3])  # shape: (3,)
y = tf.constant([4, 5, 6])  # shape: (3,)# 沿 axis=0 堆叠（默认）
stacked = tf.stack([x, y])   # shape: (2, 3)
print(stacked.numpy())
# 输出：
# [[1 2 3]
#  [4 5 6]]# 沿 axis=1 堆叠
stacked = tf.stack([x, y], axis=1)  # shape: (3, 2)
print(stacked.numpy())
# 输出：
# [[1 4]
#  [2 5]
#  [3 6]]

与 tf.concat() 的区别：

操作行为示例输入shape [2,3], [2,3]输出形状
tf.stack新增维度堆叠将两个矩阵堆叠为一个三维张量[2, 2, 3]（axis=0）
tf.concat沿现有维度拼接将两个矩阵上下拼接为一个大矩阵[4, 3]（axis=0）

tf.reduce_mean() / tf.reduce_sum() / tf.reduce_max()

tf.reduce_mean()是一个归约操作（reduction operation），用于计算张量沿指定维度的平均值

tf.reduce_mean(input_tensor,axis=None,keepdims=False,name=None
)
参数类型说明
input_tensorTensor输入张量（必须是数值类型：float16, float32, int32 等）
axisint/list/None要归约的维度（默认为 None，计算所有元素的均值）
keepdimsbool是否保留原始维度（默认为 False，降维）
namestr操作的名称（可选）
  • axis=0 表示沿每一列（垂直轴）的方向求均值，axis=1 表示沿每一行（水平轴）的方向求均值

返回值：沿指定维度求均值后的张量（维度根据 keepdims 决定）

import tensorflow as tf### 计算全局均值 ###
x = tf.constant([[1., 2.], [3., 4.]])
mean_all = tf.reduce_mean(x)  # (1+2+3+4)/4 = 2.5
print(mean_all)  # tf.Tensor(2.5, shape=(), dtype=float32)### 沿特定轴求均值 ###
# 沿 axis=0（列方向）
mean_col = tf.reduce_mean(x, axis=0)  # [(1+3)/2, (2+4)/2] = [2., 3.]
print(mean_col)  # tf.Tensor([2. 3.], shape=(2,), dtype=float32)# 沿 axis=1（行方向）
mean_row = tf.reduce_mean(x, axis=1)  # [(1+2)/2, (3+4)/2] = [1.5 3.5]
print(mean_row)  # tf.Tensor([1.5 3.5], shape=(2,), dtype=float32)# keepdims=True
mean_row = tf.reduce_mean(x, axis=1, keepdims=True)  # [[(1+2)/2], [(3+4)/2]]
print(mean_row)  # tf.Tensor([[1.5], [3.5]], shape=(2, 1), dtype=float32)

三维及以上张量归约：如输入 shape 为 (1, 2, 3)，归约的轴为 axis=-1，则输出 shape 为 (1, 2)

tf.reduce_sum() / tf.reduce_max()：

  • tf.reduce_sum()类似，用于计算张量在指定轴上的元素之和
  • tf.reduce_max() 沿着指定维度计算张量的最大值（输出维度会减少除非 keepdims=True）
# 找到概率最大的类别
def predict_class(probabilities):"""预测类别 - 找到最大概率的索引"""max_prob = tf.reduce_max(probabilities, axis=1)  # 每行的最大值predicted_class = tf.argmax(probabilities, axis=1)  # 最大值的索引return max_prob, predicted_class

tf.reduce_all() / tf.reduce_any()

执行逻辑与（AND）归约，即沿着指定的维度计算所有元素的逻辑与

tf.reduce_all(input_tensor, axis=None, keepdims=False, name=None)
  • input_tensor：输入布尔张量
  • axis：要归约的维度，如果为 None 则归约所有维度（axis=1表示沿行归约，axis=0表示沿列归约）
  • keepdims：如果为 True，保留长度为1的维度
import tensorflow as tf# 一维张量归约
tensor_1d = tf.constant([True, True, False, True])
result = tf.reduce_all(tensor_1d)
print(result.numpy())  # False# 二维张量归约
matrix = tf.constant([[True, True, True],[True, False, True],[True, True, True]])# 归约所有元素
all_elements = tf.reduce_all(matrix)
print("所有元素都为True:", all_elements.numpy())  # False
# 等价于多轴归约 tf.reduce_all(matrix, axis=[0, 1])# 沿行归约（检查每行是否全为True）
all_per_row = tf.reduce_all(matrix, axis=1)
print("每行是否全为True:", all_per_row.numpy())  # [ True False  True]# 沿列归约（检查每列是否全为True）
all_per_col = tf.reduce_all(matrix, axis=0)
print("每列是否全为True:", all_per_col.numpy())  # [ True False  True]# keepdims=True
result_keepdims = tf.reduce_all(matrix, axis=1, keepdims=True)
print(result_keepdims)
# tf.Tensor(
# [[ True]
#  [False]
#  [ True]], shape=(3, 1), dtype=bool)

特殊情况：

  • 空张量的 reduce_all 返回 True

  • 数值张量中0为False，非0为True

对比 tf.reduce_any()：

reduce_all (逻辑与)：所有元素都为True
reduce_any (逻辑或)：至少一个元素为True

tf.tile()

tf.tile()函数用于张量平铺（复制），通过沿指定维度复制张量来扩展张量的大小

tf.tile(input, multiples, name=None)
  • input：要平铺的输入张量
  • multiples：一个1维整数张量，指定每个维度复制的次数
  • name：操作的名称（可选）
import tensorflow as tf### 一维示例 ###
tensor_1d = tf.constant([1, 2, 3])    # shape=(3,)# 沿第0维复制2次
tiled_1d = tf.tile(tensor_1d, multiples=[2])
print(tiled_1d.numpy())   # [1 2 3 1 2 3]  shape=(6,)# 同时沿行和列复制
tiled_1d = tf.tile(tensor_1d, multiples=[2, 1])
print(tiled_1d.numpy())   # shape=(2, 3)
# [[1, 2, 3],
#  [1, 2, 3]]### 二维示例 ###
matrix = tf.constant([[1, 2],[3, 4]])# 沿行方向复制2次（axis=0）
tiled_rows = tf.tile(matrix, multiples=[2, 1])
print(tiled_rows.numpy())
# [[1 2]
#  [3 4]
#  [1 2]
#  [3 4]]# 沿列方向复制3次（axis=1）
tiled_cols = tf.tile(matrix, multiples=[1, 3])
print(tiled_cols.numpy())
# [[1 2 1 2 1 2]
#  [3 4 3 4 3 4]]# 同时沿行和列复制
tiled_both = tf.tile(matrix, multiples=[2, 3])
print(tiled_both.numpy())
# [[1 2 1 2 1 2]
#  [3 4 3 4 3 4]
#  [1 2 1 2 1 2]
#  [3 4 3 4 3 4]]

三维及以上张量平铺：如 shape 为 (1, 2, 2) 的 input，当 multiples=[2, 1, 1] 时，输出 shape 为 (2, 2, 2)；当 multiples=[2, 2, 3] 时，输出 shape 为 (2, 4, 6)

  • multiples=[a, b, c] 表示第0维复制a次、第1维复制b次、第2维复制c次

常用于批次数据扩展，如：

batch_data = tf.tile(single_sample, multiples=[batch_size, 1])

tf.boolean_mask()

tf.boolean_mask()函数由给定布尔掩码、根据特定轴、从输入张量中提取元素、组成新张量

tf.boolean_mask(tensor, mask, axis=None, name=None)

  • mask：布尔类型的张量，形状必须与 tensor 的前若干个维度兼容。True代表保留tensor中相应位置的元素，False代表舍弃

  • axis：可选的轴，指定应用掩码的维度。默认沿第一个维度（行）应用掩码

import tensorflow as tf### 一维示例 ###
tensor_1d = tf.constant([1, 2, 3, 4, 5])
mask_1d = tf.constant([True, False, True, False, True])result = tf.boolean_mask(tensor_1d, mask_1d)
print(result.numpy())    # [1 3 5]### 二维示例 ###
matrix = tf.constant([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
mask_2d = tf.constant([True, False, True])# 默认沿第一个维度（行）应用掩码
result = tf.boolean_mask(matrix, mask_2d)
print(result.numpy())
# [[1 2 3]
#  [7 8 9]]# 沿特定轴应用掩码
result = tf.boolean_mask(matrix, mask_2d, axis=1)
print(result.numpy())
# [[1 3]
#  [4 6]
#  [7 9]]

三维及以上张量示例：

import tensorflow as tftensor_3d = tf.constant([[[1, 2], [3, 4]],[[5, 6], [7, 8]],[[9, 10], [11, 12]]])
print(tensor_3d.shape)  # (3, 2, 2)# 沿不同轴应用掩码
mask_axis0 = tf.constant([True, False, True])  # 沿第0轴
result_axis0 = tf.boolean_mask(tensor_3d, mask_axis0, axis=0)
print(result_axis0.shape)  # (2, 2, 2)mask_axis1 = tf.constant([True, False])  # 沿第1轴
result_axis1 = tf.boolean_mask(tensor_3d, mask_axis1, axis=1)
print(result_axis1.shape)  # (3, 1, 2)

应用（处理序列数据）举例：

import tensorflow as tfsequences = tf.constant([[1, 2, 3, 0, 0],[4, 5, 0, 0, 0],[6, 7, 8, 9, 10]])
sequence_lengths = tf.constant([3, 2, 5])   # (3,)batch_size = sequences.shape[0]    # 3
max_length = sequences.shape[1]    # 5# 创建位置索引
indices = tf.range(max_length)
print("indices:\n", indices)# 为每个序列创建掩码
mask = indices < tf.expand_dims(sequence_lengths, 1)   # (3, 1)
print("tf.expand_dims(sequence_lengths, 1):\n", tf.expand_dims(sequence_lengths, 1))
print("mask:\n", mask)# 应用掩码获取有效序列元素
valid_elements = tf.boolean_mask(sequences, mask)
print("valid_elements:\n", valid_elements)

输出结果为：

indices:tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int32)tf.expand_dims(sequence_lengths, 1):tf.Tensor(
[[3][2][5]], shape=(3, 1), dtype=int32)mask:tf.Tensor(
[[ True  True  True False False][ True  True False False False][ True  True  True  True  True]], shape=(3, 5), dtype=bool)valid_elements:tf.Tensor([ 1  2  3  4  5  6  7  8  9 10], shape=(10,), dtype=int32)

tf.gather() / tf.gather_nd()

tf.gather() 用于根据索引从张量中收集元素，可以从输入张量的指定维度收集切片

tf.gather(params, indices, axis=None, batch_dims=0, name=None)
  • params：要从中收集值的输入张量
  • indices：索引张量，指定要收集的元素位置
  • axis：要收集的维度，默认为axis=0。axis=0即行，axis=1即列
  • batch_dims：指定了在哪个维度上进行批量操作，它的值表示前多少个维度被视为批量维度
import tensorflow as tf# 一维张量收集
vector = tf.constant([10, 20, 30, 40, 50, 60, 70, 80])
indices = tf.constant([0, 2, 4, 6])result = tf.gather(vector, indices)
print(result.numpy())    # [10 30 50 70]# 二维张量收集
matrix = tf.constant([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12]])   # (3, 4)# 沿行收集（axis=0，默认）
row_result = tf.gather(matrix, [0, 2], axis=0)   # (2, 4)
print(row_result.numpy())
# [[ 1  2  3  4]
#  [ 9 10 11 12]]# 沿列收集（axis=1）
col_result = tf.gather(matrix, [1, 3], axis=1)   # (3, 2)
print(col_result.numpy())
# [[ 2  4]
#  [ 6  8]
#  [10 12]]

高级用法：参数 batch_dims（批量收集）

import tensorflow as tfbatch_size = 3
seq_length = 4
feature_dim = 5# 创建批次数据和对应的索引
batch_data = tf.random.normal([batch_size, seq_length, feature_dim])   # (3, 4, 5)
# (3, 3)
batch_indices = tf.constant([[0, 2, 1],  # 第一个样本的索引[1, 3, 0],  # 第二个样本的索引[2, 1, 3]]) # 第三个样本的索引result_batch = tf.gather(batch_data, batch_indices, batch_dims=1)
print(result_batch.shape)  # (3, 3, 5)# 等价于为每个样本独立执行 gather
manual_results = []
for i in range(batch_size):manual_result = tf.gather(batch_data[i], batch_indices[i])manual_results.append(manual_result)manual_stack = tf.stack(manual_results)
print(manual_stack.shape)  # (3, 3, 5)

应用：词汇表查找（词嵌入）

import tensorflow as tfvocab_size = 10000
embedding_dim = 128# 创建词嵌入矩阵
embedding_matrix = tf.random.normal([vocab_size, embedding_dim])  # (10000, 128)# 输入单词的索引
word_indices = tf.constant([42, 123, 789, 4567])# 查找对应的词嵌入
word_embeddings = tf.gather(embedding_matrix, word_indices)
print(word_embeddings.shape)  # (4, 128)

应用：从批次中选择特定样本

import tensorflow as tfbatch_size = 8
feature_dim = 5# 创建批次数据
batch_data = tf.random.normal([batch_size, feature_dim])  # (8, 5)
labels = tf.constant([0, 1, 0, 1, 2, 0, 1, 2])# 选择类别1的样本
class_1_indices = tf.where(labels == 1)[:, 0]
class_1_data = tf.gather(batch_data, class_1_indices)print(class_1_indices.numpy())  # [1 3 6]
print(class_1_data.shape)  # (3, 5)

应用：pairwise logistic loss（带难例挖掘）

if ohem_ratio == 1.0:# 加权平均损失 (替代compute_weighted_loss), 计算公式: sum(losses * weights) / max(1, count(weights > 0))return tf.reduce_sum(losses * pairwise_weights) / tf.maximum(tf.reduce_sum(tf.cast(pairwise_weights > 0, tf.float32)),1.0)
else:# 保持每个样本对的独立损失weighted_losses = losses * pairwise_weightsk = tf.cast(tf.size(losses), tf.float32) * ohem_ratio   # 使用ohem_ratio比例的最难样本k = tf.cast(tf.round(k), tf.int32)   # 四舍五入到最接近的整数topk = tf.nn.top_k(losses, k=k)   # 选取损失最大的前k个样本对topk_weighted_losses = tf.gather(weighted_losses, topk.indices)topk_weighted_losses = tf.boolean_mask(topk_weighted_losses, topk_weighted_losses > 0)   # 只保留损失值为正（即模型预测错误）的样本进行梯度更新return tf.reduce_mean(topk_weighted_losses)   # 计算均值

对于多维索引，需要使用 tf.gather_nd()

import tensorflow as tf# 使用多维索引：选择特定的行和列组合
matrix = tf.constant([[1, 2, 3],[4, 5, 6],[7, 8, 9]])multi_indices = tf.constant([[0, 1],  # 第0行第1列[1, 2],  # 第1行第2列[2, 0]]) # 第2行第0列result_multi = tf.gather_nd(matrix, multi_indices)
print(result_multi.numpy())  # [2 6 7]

tf.scatter_nd()

tf.scatter_nd() 用于根据索引将值散布到新张量中，该张量由 indices 指示的位置更新值 updates，其他位置则填充 0，是 tf.gather_nd() 的逆操作

tf.scatter_nd(indices, updates, shape, name=None)
  • indices：二维的整数索引张量，指定要更新的位置
  • updates：要散布的值张量，表示在 indices 所指示的位置上的更新值
  • shape：输出张量的形状（一维的整数张量）
import tensorflow as tf# 一维张量散布
indices = tf.constant([[0], [2], [4]])  # 要更新的位置
updates = tf.constant([10, 30, 50])     # 要散布的值
shape = tf.constant([6])                # 输出形状result = tf.scatter_nd(indices, updates, shape)
print(result.numpy()) # [10  0 30  0 50  0]# 二维张量散布
indices = tf.constant([[0, 0], [1, 1], [2, 0]])  # [行, 列] 索引
updates = tf.constant([1, 2, 3])                 # 要散布的值
shape = tf.constant([3, 2])                      # 输出形状：3行2列result = tf.scatter_nd(indices, updates, shape)
print(result.numpy())
# [[1 0]
#  [0 2]
#  [3 0]]

特殊用法：处理重复索引 - 默认求和

indices = tf.constant([[0], [0], [1], [1], [1]])  # 重复索引
updates = tf.constant([1, 2, 3, 4, 5])           # 对应的值
shape = tf.constant([3])result = tf.scatter_nd(indices, updates, shape)
print(result.numpy())  # [3 12 0]
# 索引0: 1 + 2 = 3
# 索引1: 3 + 4 + 5 = 12
# 索引2: 0

应用：批次数据填充

# 将变长序列填充到固定长度
def pad_sequences(sequences, max_length):batch_size = len(sequences)indices = []updates = []for i, seq in enumerate(sequences):for j, val in enumerate(seq):if j < max_length:indices.append([i, j])updates.append(val)indices = tf.constant(indices)updates = tf.constant(updates)shape = tf.constant([batch_size, max_length])return tf.scatter_nd(indices, updates, shape)# 使用示例
sequences = [[1, 2, 3], [4, 5], [6, 7, 8, 9, 10]]
padded = pad_sequences(sequences, max_length=4)
print(padded.numpy())
# [[ 1  2  3  0]
#  [ 4  5  0  0]
#  [ 6  7  8  9]]

tf.slice()

用于从张量中提取切片（子张量）

# 从输入张量input中提取指定起始位置begin和大小size的子区域
tf.slice(input, begin, size, name=None)
  • begin：切片的起始位置（索引列表，索引都是从0开始的）
  • size：切片的大小列表
    • 使用-1表示提取该维度剩余的所有元素
    • 如果 size 超出实际大小，会自动调整到边界
import tensorflow as tf### 一维张量切片 ###
tensor_1d = tf.constant([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])# 从索引2开始，提取长度为5的切片
slice_1d = tf.slice(tensor_1d, begin=[2], size=[5])
print(slice_1d.numpy())  # [2 3 4 5 6]### 二维张量切片 ###
matrix = tf.constant([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12],[13, 14, 15, 16]])
# 提取第一行
first_row = tf.slice(matrix, begin=[0, 0], size=[1, 4])
print(first_row.numpy())  # [[1 2 3 4]]# 提取第二列
second_col = tf.slice(matrix, begin=[0, 1], size=[4, 1])
print(second_col.numpy())
# [[ 2]
#  [ 6]
#  [10]
#  [14]]# 使用-1表示直到末尾
slice_rest = tf.slice(matrix, begin=[1, 0], size=[-1, -1])
print(slice_rest.numpy())
# [[ 5  6  7  8]
#  [ 9 10 11 12]
#  [13 14 15 16]]

应用：时间序列窗口提取

import tensorflow as tf# 从时间序列中提取滑动窗口
time_series = tf.constant([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
window_size = 3
stride = 2# 提取多个滑动窗口
windows = []
for i in range(0, 8, stride):window = tf.slice(time_series, begin=[i], size=[window_size])windows.append(window)for i, window in enumerate(windows):print(f"窗口 {i}: {window.numpy()}")
# 窗口 0: [1 2 3]
# 窗口 1: [3 4 5]  
# 窗口 2: [5 6 7]
# 窗口 3: [7 8 9]

tf.multiply() / *

用于执行元素级乘法，对应的是数学中的哈达玛积。可以用于两个数值、两个相同shape的张量，或者一个标量和一个张量进行标量倍数的逐元素相乘

import tensorflow as tf# 标量乘法
a = tf.constant(5)
b = tf.constant(3)
result = tf.multiply(a, b)
print(result.numpy())  # 15# 向量元素级乘法
vector1 = tf.constant([1, 2, 3, 4])
vector2 = tf.constant([5, 6, 7, 8])
result = tf.multiply(vector1, vector2)
print(result.numpy())  # [ 5 12 21 32]

支持广播机制：

import tensorflow as tf# 标量与张量相乘（广播）
matrix = tf.constant([[1, 2],[3, 4]])
scalar = tf.constant(2)result = tf.multiply(matrix, scalar)
print(result.numpy())
# [[2 4]
#  [6 8]]# 不同形状张量的广播
matrix = tf.constant([[1, 2, 3],[4, 5, 6]])  # 形状: (2, 3)vector = tf.constant([10, 20, 30])  # 形状: (3,)result = tf.multiply(matrix, vector)
print(result.numpy())
# [[ 10  40  90]
#  [ 40 100 180]]

对比运算符*（两者等价）：

# 在TensorFlow中，*运算符是 tf.multiply() 的语法糖
a = tf.constant([1, 2, 3])
b = tf.constant([4, 5, 6])result1 = tf.multiply(a, b)
result2 = a * bprint("tf.multiply():", result1.numpy())  # [ 4 10 18]
print("*运算符:", result2.numpy())       # [ 4 10 18]
print("结果是否相同:", tf.reduce_all(tf.equal(result1, result2)).numpy())

应用：梯度计算

import tensorflow as tf# tf.multiply() 支持梯度计算
x = tf.constant(3.0)
y = tf.constant(4.0)with tf.GradientTape() as tape:tape.watch(x)tape.watch(y)z = tf.multiply(x, y)    # z = x * y# 计算梯度
gradients = tape.gradient(z, [x, y])
print("z = x * y =", z.numpy())           # 12.0
print("∂z/∂x =", gradients[0].numpy())    # 4.0
print("∂z/∂y =", gradients[1].numpy())    # 3.0

tf.matmul() / @

矩阵乘法（标准的线性代数矩阵乘法运算）

tf.matmul(a, b,transpose_a=False, transpose_b=False,a_is_sparse=False, b_is_sparse=False,name=None)# Python 3.5+ 支持 @运算符作为矩阵乘法
a @ b
  • a 和 b ：需要进行矩阵乘法运算的两个张量。这两个张量至少需要在最后两个维度上是矩阵
  • transpose_a 和 transpose_b ：指定了是否在执行乘法操作前先对 a 或 b 进行转置。默认值为 False，表示不进行转置
  • a_is_sparse 和 b_is_sparse ：指定了 a 或 b 是否是稀疏矩阵。在处理大型稀疏矩阵时，设置这个选项可以显著减少运算资源的需求
import tensorflow as tf# 二维矩阵乘法
A = tf.constant([[1, 2],[3, 4]])  # 2x2 矩阵
B = tf.constant([[5, 6],[7, 8]])  # 2x2 矩阵result = tf.matmul(A, B)
print(result.numpy())     # 2x2 矩阵
# [[19 22]     # 第一行: [1*5 + 2*7, 1*6 + 2*8] = [5+14, 6+16] = [19, 22]
#  [43 50]]    # 第二行: [3*5 + 4*7, 3*6 + 4*8] = [15+28, 18+32] = [43, 50]

批量矩阵乘法（批量维度会自动广播）：对每个样本独立进行矩阵乘法

批量矩阵乘法要求：
A: (..., m, n)
B: (..., n, k)  
结果: (..., m, k)
batch_A = tf.constant([[[1, 2],  # 第一个样本[3, 4]],[[5, 6],  # 第二个样本  [7, 8]]]) # 形状: (2, 2, 2)batch_B = tf.constant([[[9, 10],  # 第一个样本[11, 12]],[[13, 14], # 第二个样本[15, 16]]]) # 形状: (2, 2, 2)batch_result = tf.matmul(batch_A, batch_B)
print(batch_result.numpy())   # 形状: (2, 2, 2)
# [[[ 31  34]   # 第一个样本: [[1,2],[3,4]] × [[9,10],[11,12]]
#   [ 73  80]]
# 
#  [[181 194]   # 第二个样本: [[5,6],[7,8]] × [[13,14],[15,16]] 
#   [211 226]]]

应用：全连接层实现

def dense_layer(inputs, weights, biases):return tf.matmul(inputs, weights) + biasesinputs = tf.random.normal([batch_size, input_dim])
weights = tf.random.normal([input_dim, output_dim])
biases = tf.zeros([output_dim])output = dense_layer(inputs, weights, biases)   # (batch_size, output_dim)

应用：自注意力机制

def self_attention(Q, K, V):"""简化的自注意力计算"""# Q: (batch_size, seq_len_q, depth)# K: (batch_size, seq_len_k, depth)  # V: (batch_size, seq_len_v, depth)# 计算注意力分数 Q × Kᵀscores = tf.matmul(Q, tf.transpose(K, perm=[0, 2, 1]))  # (batch_size, seq_len_q, seq_len_k)attention_weights = tf.nn.softmax(scores, axis=-1)return tf.matmul(attention_weights, V)      # 权重 × VQ = tf.random.normal([batch_size, seq_len_q, embedding_dim])
K = tf.random.normal([batch_size, seq_len_k, embedding_dim]) 
V = tf.random.normal([batch_size, seq_len_k, embedding_dim])attention_output = self_attention(Q, K, V)  # (batch_size, seq_len_q, embedding_dim)

tf.transpose()

用于转置张量，可以重新排列张量的维度顺序

tf.transpose(a, perm=None, name='transpose')
  • perm：维度的排列顺序（一个整数列表），如果不指定则默认反转所有维度。必须包含所有维度的排列，且不能重复
import tensorflow as tf# 二维矩阵转置（最常用情况）
matrix = tf.constant([[1, 2, 3],[4, 5, 6]])
print(matrix.shape)  # (2, 3)transposed = tf.transpose(matrix)
print(transposed.numpy())
print(transposed.shape)  # (3, 2)
# [[1 4]
#  [2 5]
#  [3 6]]# 三维张量转置
tensor_3d = tf.constant([[[1, 2, 3],[4, 5, 6]],[[7, 8, 9],[10, 11, 12]]])
print(tensor_3d.shape)  # (2, 2, 3)# 指定排列顺序
print(tf.transpose(tensor_3d, perm=[2, 1, 0]).shape)   # (3, 2, 2)
print(tf.transpose(tensor_3d, perm=[1, 0, 2]).shape)   # (2, 2, 3)

应用：图像数据格式转换

import tensorflow as tf# 图像数据格式转换：NCHW <-> NHWC
# NCHW: (Batch, Channels, Height, Width)
# NHWC: (Batch, Height, Width, Channels)nchw_data = tf.random.normal([batch_size, channels, height, width])
# 转换为 NHWC格式
nhwc_data = tf.transpose(nchw_data, perm=[0, 2, 3, 1])

tf.add_n()

把多个形状且数据类型相同的Tensor按元素进行相加。比如 tf.add_n([a, b, c]) 会生成一个新的Tensor，它的每个元素都是相应的a, b, c三个Tensor中对应元素的和

import tensorflow as tfa = tf.constant([1, 2, 3])
b = tf.constant([4, 5, 6])
c = tf.constant([7, 8, 9])result = tf.add_n([a, b, c])   # 等同于tf.add_n([a+b+c]) # result的值就是：[1+4+7, 2+5+8, 3+6+9] = [12, 15, 18]

这个函数是 ​​​​​​​tf.add() ​​​​​​​函数的扩展，tf.add()函数只能对两个Tensor进行加法操作，而 ​​​​​​​tf.add_n()函数可以对多个Tensor进行加法操作

tf.divide()

tf.divide() 用于执行元素级别除法，即分别对两个张量中的每对对应元素执行除法

tf.divide(x, y, name=None)
  • 输入：x 和 y 是要执行除法操作的张量
  • 输出：一个张量，表示 x 中的元素除以 y 中的对应元素得到的结果，形状与 x 和 y 相同
import tensorflow as tf# 创建两个张量
a = tf.constant([1.0, 2.0, 3.0])
b = tf.constant([4.0, 5.0, 6.0])# 对这两个张量执行元素级别的除法
res = tf.divide(a, b)    # [1.0/4.0, 2.0/5.0, 3.0/6.0]

tf.maximum() / tf.reduce_max()

tf.maximum() 用来获取两个张量（或者张量和一个标量）之间元素级别的最大值

  • 两个张量之间：对两个相同形状的张量进行元素之间的比较，返回一个新的同形状张量，这个新的张量每个元素是原张量中对应位置上元素值较大的那个
import tensorflow as tfa = tf.constant([1.0, 2.0, 3.0])
b = tf.constant([3.0, 1.0, 2.0])# 对a和b的每个元素进行比较，取较大的值
res = tf.maximum(a, b)   # [3.0, 2.0, 3.0]
print(res)
  • 张量和一个标量之间：如 tf.maximum(a, 1.5) 将会返回一个新的张量，新张量的每个元素都是 ​​​​​​​a 张量中相同位置元素和 ​​​​​​​1.5 之间的较大值

对比 tf.reduce_max() 和 tf.maximum() ：

  • 前者是归约操作，沿着指定维度计算张量的最大值，输出维度会减少
tf.reduce_max(input_tensor, axis=None, keepdims=False, name=None)
  • 后者是元素级操作，对两个张量逐元素比较，返回每个位置的最大值，输出维度与输入相同
tf.maximum(x, y, name=None)
import tensorflow as tftensor = tf.constant([[1, 5, 3],[8, 2, 7],[4, 6, 9]])# tf.reduce_max() - 沿着维度计算最大值
# 全局最大值
global_max = tf.reduce_max(tensor)
print("全局最大值:", global_max.numpy())  # 9# 沿着行归约（axis=1） - 每行的最大值
max_per_row = tf.reduce_max(tensor, axis=1)
print("每行最大值:", max_per_row.numpy())  # [5 8 9]# 沿着列归约（axis=0） - 每列的最大值
max_per_col = tf.reduce_max(tensor, axis=0)
print("每列最大值:", max_per_col.numpy())  # [8 6 9]# 保持维度
max_per_row_keep = tf.reduce_max(tensor, axis=1, keepdims=True)
print(max_per_row_keep.numpy())
# [[5]
#  [8]
#  [9]]# tf.maximum() - 逐元素比较
# 创建另一个张量进行比较
tensor2 = tf.constant([[9, 2, 5],[3, 7, 1],[6, 4, 8]])# 逐元素取最大值
elementwise_max = tf.maximum(tensor, tensor2)
print(elementwise_max.numpy())
# [[9 5 5]
#  [8 7 7]
#  [6 6 9]]# 与标量比较
scalar_max = tf.maximum(tensor, 5)
print(scalar_max.numpy())
# [[5 5 5]
#  [8 5 7]
#  [5 6 9]]

tf.math.subtract()

tf.math.subtract() 用于进行张量相减，即对两个张量进行元素级别（element-wise）的相减

tf.math.subtract(x, y, name=None)
  • 输入：x 和 y 是需要相减的张量，必须是可以广播为相同形状的张量
  • 输出：一个与 x 和 y 同形状的新张量，新张量的每个元素是 x 和 y 中对应元素的差
import tensorflow as tfx = tf.constant([3.0, 4.0, 5.0])
y = tf.constant([1.0, 2.0, 3.0])result = tf.math.subtract(x, y)
print(result)

输出结果为：

tf.Tensor([2. 2. 2.], shape=(3,), dtype=float32)

tf.pow() / tf.exp() / tf.abs()

tf.pow() 用于对输入张量的每个元素进行指数运算，即计算 base^exponent

tf.pow(base, exponent, name=None)

用法示例：

import tensorflow as tf# 1. 标量幂运算
a = tf.constant(2.0)
b = tf.constant(3.0)
result = tf.pow(a, b)  # 2³ = 8
print(result.numpy())  # 8.0# 2. 张量逐元素幂运算
base = tf.constant([1.0, 2.0, 3.0, 4.0])
exponent = tf.constant([2.0, 3.0, 4.0, 0.5])
result = tf.pow(base, exponent)
print(result.numpy())  # [ 1.  8. 81.  2.]# 3. 广播幂运算
matrix = tf.constant([[1.0, 2.0],[3.0, 4.0]])
scalar_exp = tf.constant(2.0)
result = tf.pow(matrix, scalar_exp)  # 每个元素平方
print(result.numpy())
# [[ 1.  4.]
#  [ 9. 16.]]

tf.exp() 用于计算输入张量中每个元素的指数，即计算 e^x，其中 e 是自然对数的底数，约等于2.71828

tf.exp(x, name=None)
  • 比如，张量 [1.0, 2.0, 3.0] 使用 tf.exp() 函数，那么将得到一个新的张量 [e^1, e^2, e^3]，大致等于 [2.71828, 7.38906, 20.0855]
import tensorflow as tf# 1. 标量指数运算
x = tf.constant(1.0)
result = tf.exp(x)  # e¹ ≈ 2.718
print("e¹ =", result.numpy())  # 2.7182817# 2. 张量逐元素指数运算
tensor = tf.constant([0.0, 1.0, -1.0, 2.0])
result = tf.exp(tensor)
print(result.numpy())  # [1.         2.7182817  0.36787945 7.389056  ]# 3. 验证指数性质
x = tf.constant(2.0)
y = tf.constant(3.0)
# e² * e³ = e⁽²⁺³⁾ = e⁵
left = tf.exp(x) * tf.exp(y)
right = tf.exp(x + y)
print(tf.reduce_all(tf.equal(left, right)).numpy())
  • 在深度学习中，tf.exp() 函数往往在激活函数（如 softmax 函数）或损失函数（如交叉熵）的计算中使用。在这些场合下，exp() 函数可以帮助将模型的输出映射到一个特定的范围（比如，使用 softmax 函数可以将输出映射到0~1之间，表示概率）或者帮助优化模型的学习过程（比如，使用交叉熵作为损失函数，更好地优化分类任务）

def softmax(logits):# 数值稳定版本：减去最大值max_logits = tf.reduce_max(logits, axis=-1, keepdims=True)stable_logits = logits - max_logitsexp_logits = tf.exp(stable_logits)return exp_logits / tf.reduce_sum(exp_logits, axis=-1, keepdims=True)   # softmax概率

tf.abs() 用于计算张量中每个元素的绝对值

tf.abs(x, name=None)
  • 例如，张量 [-1.0, -2.0, 3.0] 使用 tf.abs() 函数处理它，将得到一个新的张量 [1.0, 2.0, 3.0]
  • 在深度学习中，tf.abs() 函数通常用于计算误差（如均方误差）或用于实现某些特定的激活函数（如 ReLU）
# 1. 计算误差（L1损失）
def l1_loss(predictions, targets):"""L1损失（平均绝对误差）"""absolute_errors = tf.abs(predictions - targets)return tf.reduce_mean(absolute_errors)# 2. 梯度裁剪（基于绝对值）
def clip_gradients_by_value(gradients, clip_value):clipped_gradients = []for grad in gradients:clipped_grad = tf.clip_by_value(grad, -clip_value, clip_value)clipped_gradients.append(clipped_grad)return clipped_gradients

tf.math.rint()

tf.math.rint() 用于对输入张量中的每个元素执行 “四舍五入到最近的整数” 的操作。它的名称来源于 “round to integer” 的缩写

对称性：rint(-x) = -rint(x)

tf.math.rint(x) 将输入张量 x 中的每个元素四舍五入到最接近的整数，规则如下：

  • 如果小数部分 等于 0.5，则向 最近的偶数 舍入（银行家舍入法，Bankers' Rounding）。例如2.5 → 2，3.5 → 4
  • 其他情况按 四舍五入 处理。例如 1.3 → 1，1.7 → 2

与类似函数的对比：

函数行为示例输入 [1.3, 1.5, 2.5, -1.7]
tf.math.rint()四舍五入到最近整数（0.5时向偶数舍入）[1., 2., 2., -2.]
tf.math.round()四舍五入到最近整数（0.5时远离零舍入）[1., 2., 3., -2.]
tf.floor()向下取整（向负无穷方向）[1., 1., 2., -2.]
tf.ceil()向上取整（向正无穷方向）[2., 2., 3., -1.]

为什么用 rint 而不是 round？

  • rint 的银行家舍入法（偶数舍入）在统计上更公平，能减少舍入偏差的累积
  • 例如，对 [0.5, 1.5, 2.5] 取平均：
    • rint 结果 [0., 2., 2.] → 均值 1.33
    • round 结果 [1., 2., 3.] → 均值 2.0（偏差更大）

tf.math.log1p()

tf.math.log1p() 用于计算 log(1 + x)，其中 log 是自然对数（底数是 e）

它在数值计算中比直接使用 tf.math.log(1 + x) 更加精确和稳定。比如，如果 x 是一个很小的正数（比如 1e-50），那么 1 + x 仍然接近于 1，在普通的数值精度下 log(1 + x) 可能就直接被计算为0；但如果使用 log1p 函数，就可以得到一个非零的、并且相对精确的结果

应用：pairwise_logistic_loss（完整代码参考 GitHub - tf2_pairwise_logistic_loss.py）

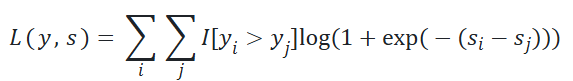
# 简化版
def pairwise_logistic_loss(labels,logits,temperature=1.0,       # 用于缩放logitshinge_margin=None):    # 正负样本对的logits最小差异# 缩放logitslogits = logits / temperature# 计算所有样本对的logits差pairwise_logits = tf.expand_dims(logits, -1) - tf.expand_dims(logits, 0)# 构建样本对掩码 (yi > yj)pairwise_mask = tf.greater(tf.expand_dims(labels, -1) - tf.expand_dims(labels, 0), 0)# hinge margin约束 (可选)if hinge_margin is not None:hinge_mask = tf.less(pairwise_logits, hinge_margin)    # logits < margin 返回true，此时才需计算losspairwise_mask = tf.logical_and(pairwise_mask, hinge_mask)# 提取有效样本对pairwise_logits = tf.boolean_mask(pairwise_logits, pairwise_mask)num_pair = tf.size(pairwise_logits)# 等价于 log(1 + exp(-pairwise_logits))，通过 relu 和 log1p 实现数值稳定性losses = tf.nn.relu(-pairwise_logits) + tf.math.log1p(tf.exp(-tf.abs(pairwise_logits)))return tf.reduce_mean(losses)

​​​​​​​tf.nn.l2_normalize()

tf.nn.l2_normalize 用于对输入的张量进行 L2范数归一化处理，即输入张量的每个元素都会除以其L2范数（也就是输入张量的所有元素的平方和的平方根），使得输出张量的 L2范数为1

tf.nn.l2_normalize(x, axis=None, epsilon=1e-12, name=None)
  • x：输入张量，希望对其进行 L2范数归一化
  • axis：进行归一化的轴的索引。例如，如果输入是一个二维张量（也就是一个矩阵），并且希望每一行都进行归一化处理，那么应设置 axis=1
  • epsilon：一个小的浮点数，加在范数的平方上，以防止除以零
import tensorflow as tfx = tf.constant([3.0, 4.0])normalized_x = tf.nn.l2_normalize(x)
print(normalized_x)

输出结果为：

tf.Tensor([0.6 0.8], shape=(2,), dtype=float32)

这是因为 x 的 L2范数是 5（根号下 3 的平方加 4 的平方），所以 x 的每个元素都除以 5，得到了新的归一化张量 normalized_x

tf.nn.relu()

tf.nn.relu() 是 "Rectified Linear Unit"（修正线性单元） 的缩写，是一个常用的激活函数

  • 引入非线性：如果没有激活函数，神经网络无论有多少层都等价于一个线性模型。ReLU 提供了非线性变换，使神经网络能够学习复杂的模式
  • 缓解梯度消失问题：与 sigmoid、tanh 等激活函数相比，ReLU 在正区间的梯度恒为 1，有效缓解了梯度消失问题
  • 计算高效：ReLU 的计算非常简单（只是比较和取最大值），相比 sigmoid/tanh，训练收敛速度更快

数学表达式如下：ReLU(x) = max(0, x)。只要输入 x 是负数，ReLU(x) 就会返回0；若输入 x 是正数或者 0，则 ReLU(x) 就直接返回 x

# ReLU 激活函数: max(0, x)
def relu_activation(x):return tf.maximum(x, 0.0)

在神经网络中的应用：

import tensorflow as tf# 方法1：作为独立的激活函数层
model = tf.keras.Sequential([tf.keras.layers.Dense(64),  # 无激活函数的全连接层tf.keras.layers.Lambda(lambda x: tf.nn.relu(x))  # 使用 ReLU
])# 方法2：更常用的方式 - 直接在 Dense 层中指定
model = tf.keras.Sequential([tf.keras.layers.Dense(64, activation='relu'),  # 直接使用 relutf.keras.layers.Dense(32, activation='relu'),tf.keras.layers.Dense(10, activation='softmax')
])

变种：LeakyReLU

  • ReLU 有 “神经元死亡” 的问题，即如果大量神经元输出为 0，可能永远无法被激活
# 标准 ReLU
output = tf.nn.relu(x)# Leaky ReLU - 负值有小的斜率，避免"神经元死亡"
output = tf.nn.leaky_relu(x, alpha=0.01)  # alpha 通常为 0.01

最佳实践：

  • 在大多数网络的隐藏层中，ReLU 是默认选择；而输出层通常根据任务选择适当的激活函数（如 softmax 用于分类，linear 用于回归）
  • 与批量归一化 BatchNorm 结合使用效果更好
  • 使用 He 初始化（论文 https://arxiv.org/abs/1502.01852）配合 ReLU
原文链接 https://cloud.tencent.com/developer/article/1587082
# 推荐：ReLU + He 初始化的配置
tf.keras.layers.Dense(64, activation='relu', kernel_initializer='he_normal')

tf.random.normal()

tf.random.normal() 用于生成正态分布（高斯分布）随机数

tf.random.normal(shape,                      # 输出张量的形状mean=0.0,                   # 正态分布的均值stddev=1.0,                 # 正态分布的标准差 (非负)dtype=tf.dtypes.float32,    # 输出数据类型seed=None,                  # 随机种子，用于重现结果name=None
)
  • mean：控制分布的中心位置

  • stddev：控制分布的扩散程度

设置随机种子保证可重现性，可以在调用 tf.random.normal() 之前加一行：

tf.random.set_seed(42)

应用：数据增强 - 向训练数据添加噪声

def training_fn():# 训练时的操作：添加噪声进行数据增强noise = tf.random.normal(tf.shape(input_data), stddev=0.1)return input_data + noise

应用：神经网络权重初始化

def initialize_dense_layer(input_dim, output_dim, initialization='he'):"""全连接层权重初始化"""if initialization == 'he':# He初始化：适合ReLU激活函数stddev = tf.sqrt(2.0 / input_dim)elif initialization == 'xavier':# Xavier初始化：适合tanh/sigmoid激活函数stddev = tf.sqrt(1.0 / input_dim)else:stddev = 0.01weights = tf.random.normal(shape=[input_dim, output_dim],mean=0.0,stddev=stddev)biases = tf.zeros([output_dim])return weights, biases

tf.expand_dims()

tf.expand_dims()用于扩展张量维度，通过在指定位置插入长度为1的新维度来改变张量的形状

tf.expand_dims(input, axis, name=None)

一维张量扩展示例：

import tensorflow as tfvector = tf.constant([1, 2, 3])
print("原始张量:", vector.shape)  # (3,)# 在不同位置扩展维度
expanded_0 = tf.expand_dims(vector, axis=0)
print("axis=0:", expanded_0.shape)  # (1, 3)
# [[1, 2, 3]]expanded_1 = tf.expand_dims(vector, axis=1)
print("axis=1:", expanded_1.shape)  # (3, 1)
# [[1], [2], [3]]expanded_neg = tf.expand_dims(vector, axis=-1)
print("axis=-1:", expanded_neg.shape)  # (3, 1)
# [[1], [2], [3]]

二维张量扩展示例：

import tensorflow as tfmatrix = tf.constant([[1, 2, 3],[4, 5, 6]])
print("原始矩阵形状:", matrix.shape)  # (2, 3)# 在不同位置扩展维度
expanded_0 = tf.expand_dims(matrix, axis=0)
print("axis=0:", expanded_0.shape)  # (1, 2, 3)expanded_1 = tf.expand_dims(matrix, axis=1)
print("axis=1:", expanded_1.shape)  # (2, 1, 3)expanded_2 = tf.expand_dims(matrix, axis=2)
print("axis=2:", expanded_2.shape)  # (2, 3, 1)expanded_neg1 = tf.expand_dims(matrix, axis=-1)
print("axis=-1:", expanded_neg1.shape)  # (2, 3, 1)expanded_neg2 = tf.expand_dims(matrix, axis=-2)
print("axis=-2:", expanded_neg2.shape)  # (2, 1, 3)

 在 pairwise logistic loss 中的应用：

import tensorflow as tf# 利用广播机制，生成所有样本对(i,j)的logits差。shape: [batch_size, batch_size]
pairwise_logits = tf.math.subtract(tf.expand_dims(logits, -1), tf.expand_dims(logits, 0))   # 前者[batch_size, 1]，后者[1, batch_size]
# 标记所有满足 yi > yj 的样本对(i,j)，返回true or false
pairwise_mask = tf.greater(tf.expand_dims(labels, -1) - tf.expand_dims(labels, 0), 0)

tf.reshape()

用于改变张量形状，可以重新排列张量的维度而不改变其数据

tf.reshape(tensor, shape, name=None)
  • tensor：要重塑的输入张量
  • shape：目标形状，可以是一个列表、元组或张量
import tensorflow as tfmatrix = tf.constant([[1, 2, 3],[4, 5, 6]])  # (2, 3)reshaped = tf.reshape(matrix, [3, 2])
print(reshaped.numpy())  # (3, 2)
# [[1 2]
#  [3 4]
#  [5 6]]

特殊形状值 -1 代表自动推断维度，但只能有一个 -1，否则无法确定维度

import tensorflow as tfvector = tf.constant([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
auto_rows = tf.reshape(vector, [-1, 3])
print(auto_rows.shape)  # (4, 3)# 当新的形状参数为 [-1] 时，意味着要将输入张量扁平化为一维张量
matrix = tf.constant([[1, 2, 3], [4, 5, 6]])  # (2, 3)
reshaped = tf.reshape(matrix, [-1])
print(reshaped)    # tf.Tensor([1 2 3 4 5 6], shape=(6,), dtype=int32)

应用：多头注意力

import tensorflow as tfdef multi_head_attention_reshape(Q, num_heads):batch_size = tf.shape(Q)[0]seq_length = tf.shape(Q)[1]depth = tf.shape(Q)[2]# 重塑为 (batch_size, seq_length, num_heads, depth_per_head)depth_per_head = depth // num_headsreshaped_Q = tf.reshape(Q, [batch_size, seq_length, num_heads, depth_per_head])# 转置为 (batch_size, num_heads, seq_length, depth_per_head)transposed_Q = tf.transpose(reshaped_Q, [0, 2, 1, 3])return transposed_Q# 示例
Q = tf.random.normal([2, 5, 64])  # (batch, seq_len, depth)
num_heads = 8
multi_head_Q = multi_head_attention_reshape(Q, num_heads)
print("原始Q形状:", Q.shape)          # (2, 5, 64)
print("多头Q形状:", multi_head_Q.shape)  # (2, 8, 5, 8)

tf.range()

tf.range 用于创建一个包含等差数列的一维张量，类似于 Python 内置的 range() 函数，但返回的是 TensorFlow 张量

tf.range(start, limit=None, delta=1, dtype=None, name=None)
  • start：序列的起始值（包含）
  • limit：序列的结束值（不包含）
  • delta：步长，默认为 1，可以为负数
  • dtype：输出张量的数据类型
import tensorflow as tfindices = tf.range(5)
print(indices)

输出结果为：

tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int32)

应用：Transformer模型中的位置编码（提供序列中每个位置的位置信息）

def positional_encoding(sequence_length, d_model):# [:, tf.newaxis]：增加一个维度，从 (seq_len,) 变为 (seq_len, 1) 的列向量position = tf.range(sequence_length, dtype=tf.float32)[:, tf.newaxis]  # (seq_len, 1)div_term = tf.exp(tf.range(0, d_model, 2, dtype=tf.float32) *   # 偶数索引-(tf.math.log(10000.0) / d_model))# 原公式：exp(2i * (-ln(10000)/d_model))# = exp(-2i * ln(10000)/d_model)# = (exp(ln(10000)))^(-2i/d_model)# = 10000^(-2i/d_model)angle_rates = position * div_term   # (seq_len, d_model/2)sin_encoding = tf.sin(angle_rates)  # 偶数列 - 正弦函数cos_encoding = tf.cos(angle_rates)  # 奇数列 - 余弦函数# 交错拼接正弦和余弦positional_encoding = tf.stack([sin_encoding, cos_encoding], axis=2)  # (seq_len, d_model/2, 2)positional_encoding = tf.reshape(positional_encoding, [sequence_length, d_model])  # (seq_len, d_model)return positional_encoding

应用：创建 one-hot 编码

num_classes = 5
labels = tf.constant([0, 2, 4])class_range = tf.range(num_classes)
print(class_range.numpy())  # [0 1 2 3 4]# 创建 one-hot 编码
one_hot = tf.cast(tf.equal(labels[:, tf.newaxis], class_range), tf.float32)
print(one_hot.numpy())
# [[1. 0. 0. 0. 0.]
#  [0. 0. 1. 0. 0.]
#  [0. 0. 0. 0. 1.]]

tf.sequence_mask()

tf.sequence_mask() 用于创建序列掩码，根据序列长度生成布尔掩码，常用于处理变长序列数据

tf.sequence_mask(lengths, maxlen=None, dtype=tf.dtypes.bool, name=None)
  • lengths：序列长度张量，1D 整数张量。输入形状为 [batch_size]
  • maxlen：最大序列长度，如果不指定则使用 lengths 中的最大值
  • dtype：输出掩码的数据类型，默认为 tf.bool，也可以为 tf.int32/tf.float32

  • 输出掩码形状为 [batch_size, maxlen]

import tensorflow as tf# 创建序列长度掩码
sequence_lengths = tf.constant([3, 5, 2, 4])
mask = tf.sequence_mask(sequence_lengths, 5)
print(mask.numpy())# [[ True  True  True False False]
#  [ True  True  True  True  True]
#  [ True  True False False False]
#  [ True  True  True  True False]]

应用：获取序列的实际长度 -> 创建掩码 -> 在模型计算中应用掩码 -> 在损失计算中忽略填充位置

import tensorflow as tf# 序列的实际长度
sequence_lengths = tf.constant([2, 4, 3])# 创建掩码
mask = tf.sequence_mask(sequence_lengths, maxlen=5)    # shape=(3, 5)# 在模型计算中应用掩码
lstm_output = tf.random.normal([3, 5, 8])  # 模拟LSTM输出 (batch_size, seq_len, hidden_size)
mask_float = tf.cast(mask, tf.float32)[:, :, tf.newaxis]   # (3, 5, 1)
masked_output = lstm_output * mask_float   # (3, 5, 8)# 在损失计算中忽略填充位置
# 真实标签
true_labels = tf.constant([[10, 20, 0, 0, 0],[30, 40, 50, 60, 0], [70, 80, 90, 0, 0]
])# 预测标签  
pred_labels = tf.constant([[12, 18, 5, 8, 3],[28, 42, 48, 65, 2],[72, 78, 85, 4, 1]
])# 计算MSE损失（只计算有效位置）
mse = tf.square(true_labels - pred_labels)
masked_mse = mse * tf.cast(mask, tf.float32)
# 只对有效位置求平均
valid_positions = tf.reduce_sum(tf.cast(mask, tf.float32))
total_loss = tf.reduce_sum(masked_mse) / valid_positions

输出结果为：

# mse
tf.Tensor(
[[ 4  4 25 64  9][ 4  4  4 25  4][ 4  4 25 16  1]], shape=(3, 5), dtype=int32)# masked_mse
tf.Tensor(
[[ 4  4  0  0  0][ 4  4  4 25  0][ 4  4 25  0  0]], shape=(3, 5), dtype=int32)# valid_positions
tf.Tensor(9, shape=(), dtype=int32)# total_loss
tf.Tensor(8.666666666666666, shape=(), dtype=float64)

相关函数：

  • 结合 tf.boolean_mask() 提取有效元素
  • 使用 tf.where() 应用掩码，即根据条件选择元素

tf.nn.embedding_lookup()

tf.nn.embedding_lookup() 用于词嵌入查找，它根据索引从嵌入矩阵中查找对应的嵌入向量

tf.nn.embedding_lookup(params, ids, max_norm=None, name=None)
  • params：嵌入矩阵，形状为 [vocab_size, embedding_dim]
  • ids：要查找的索引，可以是标量、向量或更高维度的张量
  • max_norm：如果提供，会对查找的嵌入向量进行 L2归一化
  • 输出形状为 ids.shape + [embedding_dim]

如：params 是一个形状为 [vocab_size, embedding_dim] 的词嵌入矩阵，ids 是一个形状为[batch_size, sequence_length] 的整数张量，那么这个操作将会返回一个形状为 [batch_size, sequence_length, embedding_dim] 的向量。这个向量就是每个ID在词嵌入矩阵中对应的向量

其他常用

class、__init__、call

Python用法，非Tensorflow

在 Python 中，当我们定义一个类时，通常会用到 __init__ 和 call 这两个特殊的方法

  • __init__ 方法：此方法在 Python 中被称为初始化方法或构造器方法。当一个类被实例化（即创建一个类的对象）时，就会自动调用这个方法。通常在 __init__ 方法中定义那些在对象创建时就需要被初始化的属性
  • call 方法：此方法在 Python 中被称为可调用方法。当一个对象像函数那样被使用时，就会自动触发 call 方法

例如，我们定义一个名为 Model 的类，并使用 __init__ 方法为其初始化一个属性（name 是在创建 Model 类的对象时需要传入的参数）；同时可以为上述的 Model 类添加一个 call 方法（可以像调用函数一样调用 Model 类的对象，并向其传递参数 x）

class Model:def __init__(self, name):self.name = namedef __call__(self, x):return f'Model {self.name} process {x}'

这两个方法可以帮我们理解在类中需要哪些输入参数。在 __init__ 方法中定义的是在对象创建时需要的输入，而在 __call__ 方法中定义的是在对象被函数式调用时需要的输入

# 使用上述的 Model 类为例
model = Model('Example')  # 创建对象时，需要一个名为 `name` 的输入
output = model('input')   # 对象被函数式调用时，需要一个名为 `x` 的输入

assign_sub / assign

assign_sub 用于对变量的值进行就地（in-place）减法操作，即将变量的值减去指定的值，并将结果重新赋值给该变量。通常用于优化算法中更新模型参数（如权重）或优化器中的状态变量

tf.Variable.assign_sub(value)
  • value：要减去的值，可以是一个标量、张量或与变量形状相同的张量
  • 返回更新后的变量

特点：

  • 就地操作：assign_sub 会直接修改变量的值，而不是创建一个新的变量
  • 仅适用于变量：assign_sub 只能用于 tf.Variable 类型的对象，不能用于普通的张量（tf.Tensor）
  • 自动类型转换：如果 value 的类型与变量的类型不同，会自动进行类型转换
import tensorflow as tf# 创建一个变量
x = tf.Variable(10.0)# 使用 assign_sub 减去一个值
x.assign_sub(3.0)
print("Updated x:", x.numpy())    # 7.0

在训练神经网络时，assign_sub 通常用于更新模型参数。例如，在使用梯度下降法时，可以用 assign_sub 来更新权重：

import tensorflow as tf# 创建一个变量（模拟权重）
weight = tf.Variable(5.0)
# 模拟梯度
gradient = 2.0
# 学习率
learning_rate = 0.1# 更新权重：weight = weight - learning_rate * gradient
weight.assign_sub(learning_rate * gradient)
print("Updated weight:", weight.numpy())   # 4.8

assign_sub 是对变量进行减法操作，而 assign 是直接为变量赋值，例如：

x.assign(7.0)   # 将 x 的值设置为 7.0

tf.float32.min

tf.float32.min 是 TensorFlow 的一个标量，表示 float32 数据类型能够表示的最小正数。常作为数值稳定性的阈值，用于下溢保护

def stable_softmax(logits):"""数值稳定的 softmax"""# 减去最大值提高数值稳定性max_logits = tf.reduce_max(logits, axis=-1, keepdims=True)stable_logits = logits - max_logits# 计算指数exp_logits = tf.exp(stable_logits)# 保护下溢exp_logits = tf.maximum(exp_logits, tf.float32.min)# 归一化return exp_logits / tf.reduce_sum(exp_logits, axis=-1, keepdims=True)

logging.info()

Python用法，非Tensorflow

Python logging 模块定义了多个日志级别（按严重程度递增）：

级别数值函数用途
DEBUG10logging.debug()详细的调试信息
INFO20logging.info()确认程序按预期运行
WARNING30logging.warning()表示意外情况，但程序仍能运行
ERROR40logging.error()由于严重问题，程序无法执行某些功能
CRITICAL50logging.critical()严重错误，程序本身可能无法继续运行

logging.info() 的级别为 20，通常用于记录程序正常运行时的关键信息。注意，默认的日志级别是 WARNING（30）才会输出：

import logging# 设置日志级别为 INFO
logging.basicConfig(level=logging.INFO)logging.info("程序启动")
logging.debug("这条调试消息不会显示")  # 因为级别低于 INFO
logging.warning("这是一条警告消息")    # 这会显示

完整配置：

import logginglogging.basicConfig(level=logging.INFO,# %(asctime)s - 时间戳# %(name)s - 记录器名称# %(levelname)s - 日志级别# %(message)s - 日志消息format='%(asctime)s - %(name)s - %(levelname)s - %(message)s',datefmt='%Y-%m-%d %H:%M:%S',filename='app.log',  # 可选：输出到文件filemode='a'         # 可选：追加模式
)

  • print() 只是临时调试，logging.info() 提供完整的日志管理

在深度学习模型中的应用：

import logging
import tensorflow as tfdef train_model():logging.basicConfig(level=logging.INFO,format='%(asctime)s - %(levelname)s - %(message)s')logging.info("开始模型训练")# 加载数据logging.info("加载训练数据")(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()logging.info(f"训练数据形状: {x_train.shape}")# 构建模型logging.info("构建神经网络模型")model = tf.keras.Sequential([tf.keras.layers.Flatten(input_shape=(28, 28)),tf.keras.layers.Dense(128, activation='relu'),tf.keras.layers.Dense(10)])# 编译模型logging.info("编译模型")model.compile(optimizer='adam',loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),metrics=['accuracy'])# 训练模型logging.info("开始训练循环")model.fit(x_train, y_train, epochs=5, verbose=0)logging.info("模型训练完成")# 评估模型logging.info("评估模型性能")test_loss, test_acc = model.evaluate(x_test, y_test, verbose=0)logging.info(f"测试准确率: {test_acc:.4f}")train_model()
http://www.dtcms.com/a/565100.html

相关文章：

  • 《备忘录模式：软件设计中的经典模式解析与应用》
  • meta-llama-3-8B下载失败解决。
  • [N_154]基于springboot酒店预订管理系统
  • 从语音唤醒到边缘智能：ESP32-S3 + TensorFlow Lite Micro 的技术潜力
  • wordpress 订阅号推送乐陵网站优化
  • 【LeetCode 每日一题】1768. 交替合并字符串
  • 大模型长文生成中的幻觉与事实性：研究进展综述
  • 在苹果设备上安装描述文件的完整步骤指南
  • 展示形网站怎么建自己可以制作微信小程序吗
  • Qwen3-VL微调自定义OCR任务
  • 【5】理解GUID和Handle：解锁UEFI驱动和应用程序的钥匙
  • [手机AI开发sdk] docs | AidLearning平台(四合一环境)
  • CTFHub XSS通关：XSS-过滤关键词
  • Java设计模式精讲---简单工厂模式
  • Spring Boot + EasyExcel 枚举转换器：通用方案
  • Pandas-之数据合并与连接
  • 大数据毕业设计项目推荐 基于大数据的广西医疗机构数据可视化分析系统 1.85w条数据【大数据毕业设计项目选题】
  • Node.Js 实现模板生成Word、Word转Pdf文件、Excel生成、上传和下载
  • 山西省建设监理协会官方网站好书推荐ppt模板免费下载
  • 机器学习中的Hello World：线性回归（一）
  • RT-DETR解码模块(Decoder)
  • 做炫舞情侣头像动态图网站建设公司网站怎么弄
  • 诚通凯胜生态建设有限公司网站莆田企业网站建设
  • IVWorks率先将8英寸GaN纳米线片商业化
  • ip网段扫描机器shell脚本
  • 智能家居品牌出海新打法：用海外网红营销讲好“未来生活剧本”
  • 做网站有效果吗网络推广公司方案
  • 基于ROS与YOLOv3的智能采购机器人设计（智能车创意组-讯飞智慧生活组）
  • 优化Elasticsearch批量写入性能：从单分片瓶颈到多索引架构
  • 高效文献阅读与笔记整理方法：从 筛选 到 3Pass 精读