数据结构——三十七、关键路径(王道408)
文章目录
- 前言
- 一.AOE网
- 1.标准定义
- 2.通俗理解
- 3.性质
- 4.两个相关概念
- 二.关键路径概念及其求解方法
- 1.关键路径的概念
- 2.几个相关概念
- 1.最早发生时间与最早开始时间
- 2.最迟发生时间与最迟开始时间
- 3.时间余量,关键活动与关键路径
- 3.求关键路径的步骤
- 1.思路
- 2.步骤
- 三.关键活动,关键路径的特性
- 四.知识回顾与重要考点
- 结语
前言
AOE网是一种用顶点表示事件、有向边表示活动、边权值表示活动耗时的有向图。关键路径是AOE网中具有最大路径长度的路径,决定整个工程的最短完成时间。求解关键路径需要分步骤计算各事件的最早/最迟发生时间(ve/vl)和各活动的最早/最迟开始时间(e/l)。其中时间余量d=l-e为零的活动为关键活动,由关键活动组成的路径即为关键路径。通过拓扑排序计算ve,逆拓扑排序计算vl,最终可确定关键路径。
一.AOE网
1.标准定义
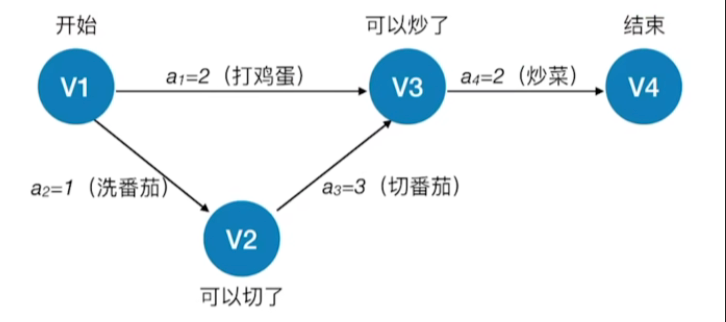
- 在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动网络的网络,简称AOE网(Activity On Edge NetWork)
2.通俗理解
- 各个顶点呢表示的是一个一个的事件
- 这些一个一个的活动是需要持续一段时间的而所谓的事件的发生其实就是一瞬间的事情,它只是一个时刻而已
3.性质
- 只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始;
- 如:只有上图中的开始这个事件发生了之后,我们才能进行打鸡蛋和洗番茄这两个活动
- 只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生。另外,有些活动是可以并行进行的;
- 如:我们只有做完打鸡蛋和切番茄这两个活动之后才会发生可以炒了这个事件
- 如:像番茄炒蛋这件事,可以同时有一个人在打鸡蛋,另一个人在洗番茄,但是像洗番茄和切番茄这两件事,肯定没办法同时进行,因为我们只有洗番茄,洗完了之后才可以开始切
4.两个相关概念
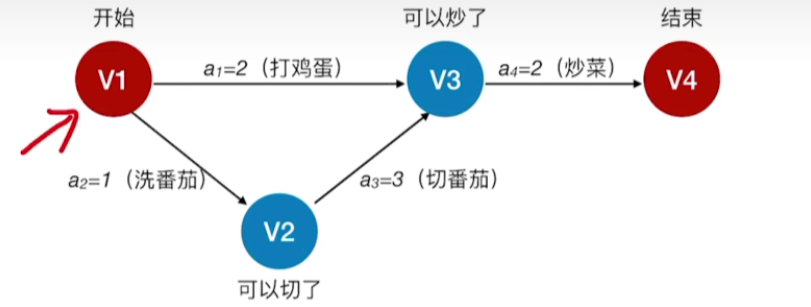
- 在AOE网中仅有一个入度为0的顶点,称为开始顶点(源点),它表示整个工程的开始;
- 也仅有一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。
二.关键路径概念及其求解方法
1.关键路径的概念
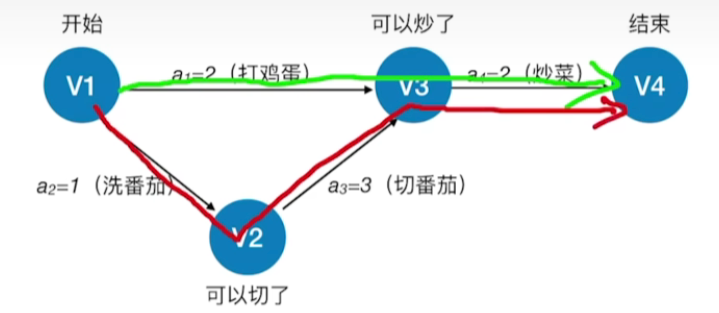
- 从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动
- 如上图是红色的路径为关键路径
- 完成整个工程的最短时间就是关键路径的长度,若关键活动不能按时完成,则整个工程的完成时间就会延长
- 如上图的红色路径,我可以在开始的时候同时进行打鸡蛋和洗番茄,在洗完番茄之后马上切番茄在这个过程中打鸡蛋也被处理掉了,然后就可以炒了,最后在抄完菜后结束.可以看出打鸡蛋的时间被我们的关键路径所用的时间覆盖了,因此关键路径的耗费时间就是整个工程的最短时间
2.几个相关概念
1.最早发生时间与最早开始时间
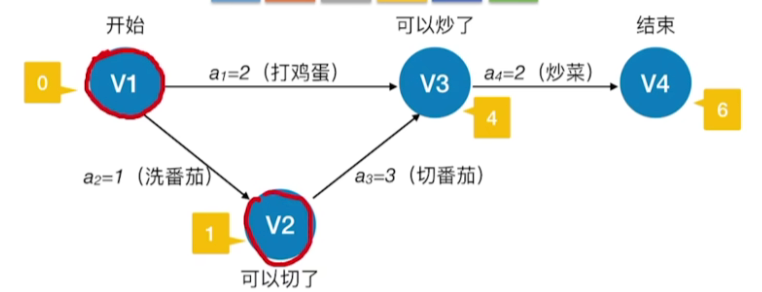
- 事件vkv_kvk的最早发生时间ve(k)ve(k)ve(k)——决定了所有从vkv_kvk以开始的活动能够开工的最早时间(图中标黄的数字)
- 活动aia_iai的最早开始时间e(i)e(i)e(i)——指该活动弧的起点所表示的事件的最早发生时间(其实每个活动最早可以开始的时间,就是他的弧尾所连接的这个事件的最早发生时间,因此也是图中标黄的数字)
- 如:比如洗番茄这个活动最早可以从0这个时刻开始,然后切番茄这个活动最早也就可以从1这个时刻开始
2.最迟发生时间与最迟开始时间
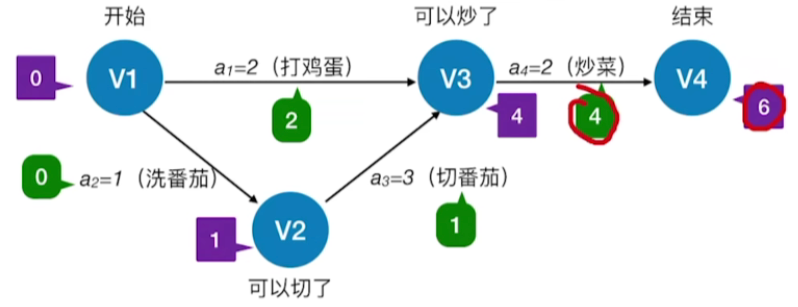
- 事件vkv_kvk的最迟发生时间vl(k)vl(k)vl(k)——它是指在不推迟整个工程完成的前提下,该事件最迟必须发生的时间(图中标紫的数字)。
- 活动aia_iai的最迟开始时间l(i)l(i)l(i)——它是指该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差(图中标绿的数字)。
- 如:打鸡蛋这个活动,他后面的这个事件v3必须在4这个时刻发生,而打鸡蛋总共又需要消耗两分钟的时间,所以我们最晚可以2这个时刻开始打鸡蛋,然后到4这个时刻,刚好可以保证不拖累v3这个事件的发生
3.时间余量,关键活动与关键路径
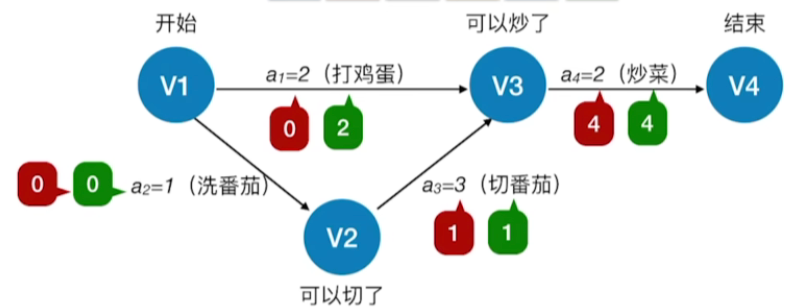
- 活动aia_{i}ai的时间余量d(i)=l(i)−e(i)d(i)=l(i)-e(i)d(i)=l(i)−e(i),表示在不增加完成整个工程所需总时间的情况下,活动aia_{i}ai可以拖延的时间
- 如上图的打鸡蛋这个活动,最早开始时间为0,最晚开始时间为2,其活动余量就为2
- 若一个活动的时间余量为零,则说明该活动必须要如期完成,d(i)=0d(i)=0d(i)=0即l(i)=e(i)l(i)=e(i)l(i)=e(i)的活动aia_{i}ai是关键活动,由关键活动组成的路径就是关键路径
- 如上图的洗番茄,切番茄,炒菜都是关键活动
3.求关键路径的步骤
1.思路
- 求某一事件的最早发生时间ve()
- 根据ve()推出对应活动的最早发生时间e()
- 求某一事件的最迟发生时间vl()
- 根据vl()推出对应活动的最迟发生时间l()
- 有了各个活动的最早发生时间和最迟发生时间之后,我们就可以算出时间余量d(),时间余量为0的那些活动就是关键活动
- 找到了这些关键活动也就找到了各个边,我们就可以确定最终的关键路径
2.步骤
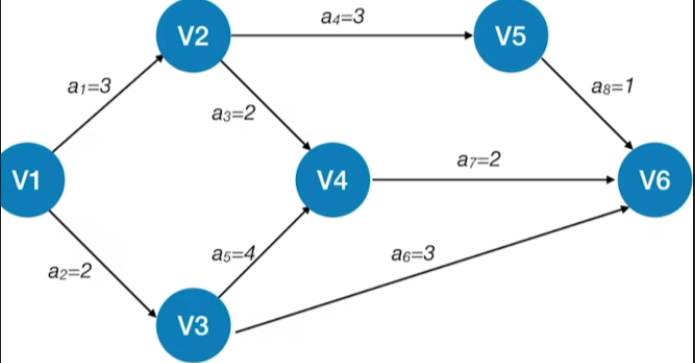
- 求所有事件的最早发生时间ve()
- 按拓扑排序序列(找到这个拓扑排序序列,只是为了让你的计算过程能够有条不紊),依次求各个顶点的ve(k):{ve(源点)=0ve(k)=Max{ve(j)+Weight(vj,vk)},vj为vk的任意前驱\begin{cases} ve(源点)=0 \\ ve(k)=Max\{ve(j)+Weight(v_j,v_k)\}, &v_j为v_k的任意前驱\end{cases}{ve(源点)=0ve(k)=Max{ve(j)+Weight(vj,vk)},vj为vk的任意前驱
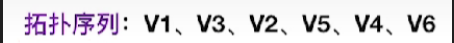
- 那首先对于开始这个顶点V1,它的最早发生时间肯定是0
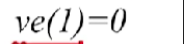
- 按照拓扑序列,接下来求V3,除了原点之外其他的所有的顶点,肯定都至少会有一个直接前驱,那像V3这个顶点,他有可能的最早发生时间,就是它前驱顶点V1的最早发生时间,加上这个活动所需要消耗的时间,因此ve(3) = 0 + 2 = 2
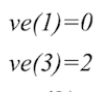
- 接下来也是一样的操作,一直到V4,结果如下
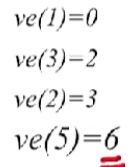
- V4这个顶点和之前的几个顶点不一样,因为它有两个直接前驱,分别是V2和V3
- 因为V2事件最早有可能在2时刻发生,而发生这个时刻之后,你还需要经过时长为2的活动,才有可能让V4这个事件发生,因此从V2这边来看,最早也就是5这个时刻有可能发生V4
- 同样的分析,从V2这边来看,最早也就是6这个时刻有可能发生V4,因为只有所有的指向V4的活动都结束了之后,V4这个事件才有可能发生,那显然我们应该取更大的这个值,也就是ve(4)=max{ve(2)+2,ve(3)+4}=6ve(4)=max\{ve(2)+2,ve(3)+4\}=6ve(4)=max{ve(2)+2,ve(3)+4}=6
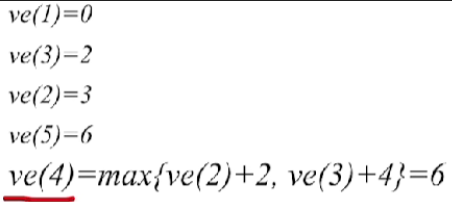
- 后面的操作都是类似的,不再赘述,最终结果如下:
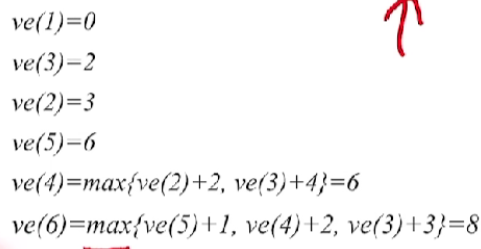
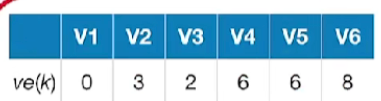
- 按拓扑排序序列(找到这个拓扑排序序列,只是为了让你的计算过程能够有条不紊),依次求各个顶点的ve(k):{ve(源点)=0ve(k)=Max{ve(j)+Weight(vj,vk)},vj为vk的任意前驱\begin{cases} ve(源点)=0 \\ ve(k)=Max\{ve(j)+Weight(v_j,v_k)\}, &v_j为v_k的任意前驱\end{cases}{ve(源点)=0ve(k)=Max{ve(j)+Weight(vj,vk)},vj为vk的任意前驱
- 求所有事件的最迟发生时间vl()
- 按逆拓扑排序序列,依次求各个顶点的vl(k):{vl(汇点)=ve(汇点)vl(k)=Min{vl(j)−Weight(vk,vj)},vj为vk的任意后继\begin{cases} vl(汇点)=ve(汇点) \\ vl(k)=Min\{vl(j)-Weight(v_k,v_j)\}, &v_j为v_k的任意后继\end{cases}{vl(汇点)=ve(汇点)vl(k)=Min{vl(j)−Weight(vk,vj)},vj为vk的任意后继

- 那首先第一个事件是V6(汇点),那汇点所允许的最迟发生时间其实和它的最早发生时间是一样的,即vl(6) = ve(6) = 8
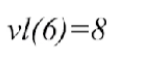
- 按照之前的逆拓扑排序,接下来计算V5,V6要在8发生,那么V5到V6中间的这个活动需要消耗1的时间,所以V5这个事件,至少需要在7这个时刻发生,也就是用vl(5)=vl(6)−a8=7vl(5) = vl(6)-a_8 = 7vl(5)=vl(6)−a8=7,a8a_8a8是V5->V6的权值
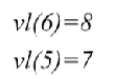
- 接下来也是一样的,一直到V2
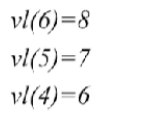
- V2和之前不太一样,因为它有两个直接的后继,先看V2->V5这个活动,V5这个事件必须在7这个时刻发生,而在V5之前又必须进行a4a_4a4这个活动,这个活动需要消耗3的时间,所以从V2->V5来看,V2这个事件至少应该在vl(2)=vl(5)−a4=4vl(2) = vl(5) - a_4 = 4vl(2)=vl(5)−a4=4这个时刻发生
- 同样的分析,V2->V4事件至少应该在vl(2)=vl(4)−a3=4vl(2) = vl(4) - a_3 = 4vl(2)=vl(4)−a3=4这个时刻发生,我们取最小值4
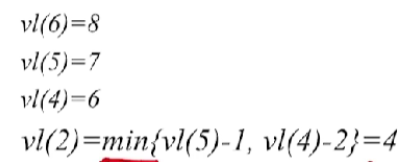
- 后面的操作和以上的操作类似,不做赘述,最终结果为:

- 事件的最早发生时间图:
- 按逆拓扑排序序列,依次求各个顶点的vl(k):{vl(汇点)=ve(汇点)vl(k)=Min{vl(j)−Weight(vk,vj)},vj为vk的任意后继\begin{cases} vl(汇点)=ve(汇点) \\ vl(k)=Min\{vl(j)-Weight(v_k,v_j)\}, &v_j为v_k的任意后继\end{cases}{vl(汇点)=ve(汇点)vl(k)=Min{vl(j)−Weight(vk,vj)},vj为vk的任意后继
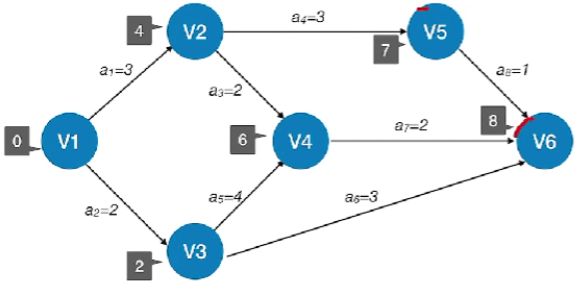
- 求所有活动的最早发生时间 e()
- 其实每一个活动的最早发生时间就是这个活动的弧尾所连的这个事件的最早发生时间,即若边<vk,vj>< v_{k},v_{j}><vk,vj>表示活动ala_{l}al,则有e(i)=ve(k)e(i)=ve(k)e(i)=ve(k)
- 根据之前求出的ve()得到e()
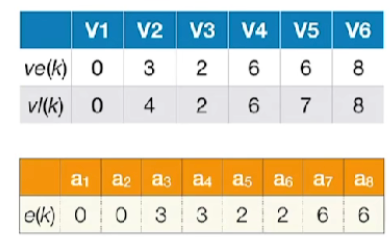
- 事件的最迟发生时间图:
- 求所有活动的最迟发生时间 I( )
- 求各个事件的最迟发生时间,其实就是这条弧所指向的这个节点的最晚发生时间,减掉这条弧的权值,即若边 <vk,vj>< v_{k}, v_{j}><vk,vj> 表示活动 aia_{i}ai, 则有 l(i)=vl(j)−Weight(vk,vj)l(i)=vl(j)-\text{Weight}(v_{k},v_{j})l(i)=vl(j)−Weight(vk,vj)
- 比如V6这个事件,你最晚可以在8这个时刻发生,那么a8a_8a8这个活动,总共需要消耗1的时间,所以这个活动最晚可以开始的时间,应该是8 - 1 = 7
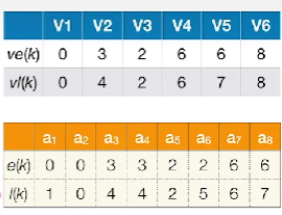
- 求所有活动的时间余量 d( )
- d(i)=I(i)-e(i)
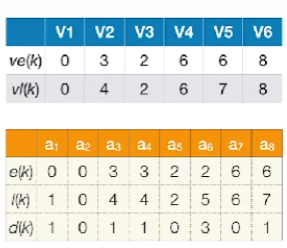
- d(i)=I(i)-e(i)
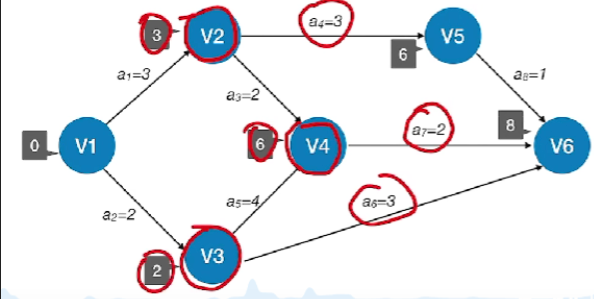
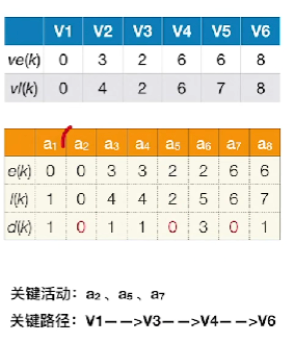
- 发现a2,a5,a7a_2,a_5,a_7a2,a5,a7这几个活动的时间余量都是0,都是关键活动,相组合就是这个AOE网的关键路径
三.关键活动,关键路径的特性
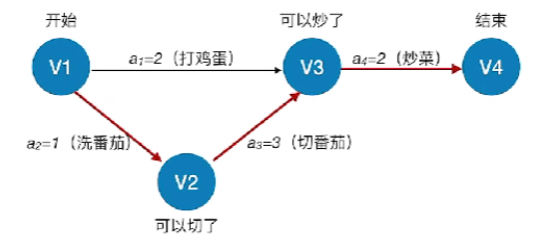
- 若关键活动耗时增加,则整个工程的工期将增长
- 缩短关键活动的时间,可以缩短整个工程的工期
- 当缩短到一定程度时,关键活动可能会变成非关键活动,这时关键路径也会改变
- 如:上图的切番茄是一个关键活动,但是如果我们把它的活动时间a3a_3a3改为0.5,那么它就不是关键活动了,因为关键路径更改为V1->V3->V4了
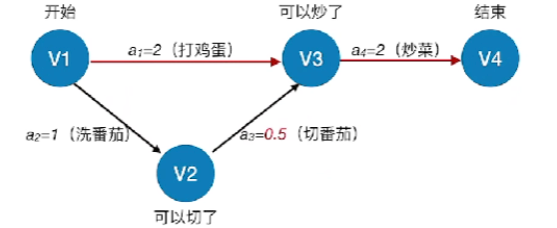
- 如:上图的切番茄是一个关键活动,但是如果我们把它的活动时间a3a_3a3改为0.5,那么它就不是关键活动了,因为关键路径更改为V1->V3->V4了
- 可能有多条关键路径,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
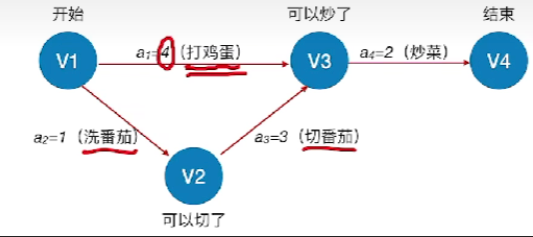
如:上图,打鸡蛋的时间和洗番茄与切番茄加起来的时间相同,那么这两条路径都是关键路径,只缩短某一条关键路径上的工期并不能缩短整个工程的工期,除非你把打鸡蛋和切番茄或者洗番茄的时间都压缩或者你可以加快炒菜这个活动的时间
四.知识回顾与重要考点

结语
一更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页
