算法：从特殊到一般——拆解两两交换链表节点的递归解法

从特殊到一般：拆解两两交换链表节点的递归解法

力扣链接

在链表操作中，“两两交换相邻节点” 是一道经典题目。要求不修改节点值，只通过指针操作完成交换，且返回交换后的头节点。很多人初次接触时会被指针的指向关系绕晕，其实只要从最简单的场景入手，逐步推演规律，就能轻松掌握其核心逻辑。本文将从 1 个、2 个、3 个节点的特殊情况开始，带你抽象出通用的递归解法。

一、从简单场景开始：1-2-3 个节点的交换逻辑

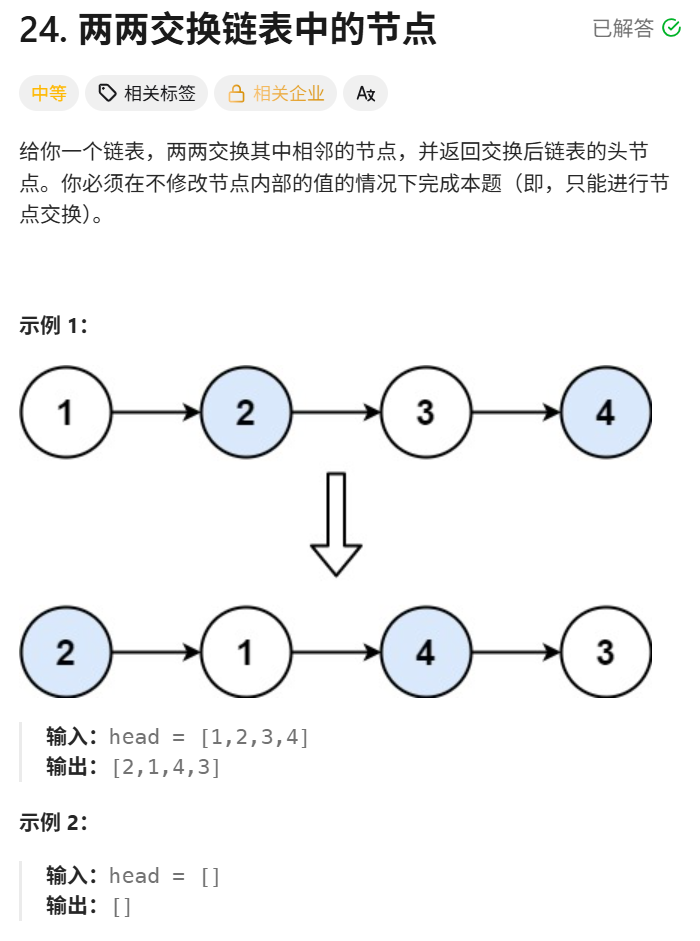
先明确问题：给定一个单链表，需要两两交换相邻的节点。例如输入1→2→3→4，输出2→1→4→3。交换时只能操作指针，不能修改节点的val值。

1. 特殊情况 1：空链表或只有 1 个节点

这是最基础的场景，无需任何交换操作：

• 若链表为空（head = null），直接返回null；
• 若只有 1 个节点（head→null），直接返回该节点。

这就是递归的终止条件—— 当剩余节点不足 2 个时，无法交换，直接返回当前头节点。

2. 特殊情况 2：有 2 个节点（1→2→null）

这是能进行交换的最小场景，步骤如下：

• 定义cur = 1（当前节点），next = 2（下一个节点）；
• 交换指针：让next的next指向cur（即2→1）；
• 让cur的next指向null（因为交换后1成为尾节点）；
• 返回新的头节点next（即2）。

交换后结果为2→1→null，符合预期。此时我们发现：处理 2 个节点时，只需交换两者的指向，并让第一个节点指向后续剩余节点（这里后续为空）。

3. 特殊情况 3：有 3 个节点（1→2→3→null）

当节点数为 3 时，需要先处理前 2 个节点，再处理剩余的 1 个节点（无需交换）。步骤分解如下：

1. 交换前 2 个节点：
   • cur = 1，next = 2，剩余节点tail = 3；
   • 交换后2→1，此时需要让1的next指向剩余节点的处理结果；
2. 处理剩余节点：
   • 剩余节点tail = 3（只有 1 个节点），根据终止条件，直接返回3；
   • 因此1的next指向3，形成2→1→3→null；
3. 返回新头节点2。

最终结果为2→1→3→null，符合两两交换的规则（前两个交换，第三个保持原位）。

4. 特殊情况 4：有 4 个节点（1→2→3→4→null）

这是示例中的场景，更能体现递归的思路：

1. 交换前 2 个节点：
   • cur = 1，next = 2，剩余节点tail = 3→4；
   • 交换后2→1，1的next需要指向tail的处理结果；
2. 递归处理剩余节点：
   • 对tail = 3→4调用交换逻辑，得到4→3→null；
   • 因此1的next指向4，形成2→1→4→3→null；
3. 返回新头节点2。

这里明显看到：处理 4 个节点时，先交换前 2 个，再递归处理后 2 个，最后把两部分结果连接起来。

二、从特殊到一般：抽象通用递归逻辑

通过上述场景推演，我们可以总结出通用规律：对于任意链表，都可以拆成 “前 2 个节点” 和 “剩余节点” 两部分，先交换前 2 个，再递归处理剩余节点，最后将两部分结果连接。

1. 明确终止条件

当链表剩余节点不足 2 个时（head == null或head->next == null），无法交换，直接返回head。这是递归的 “出口”，对应代码：

if(head == nullptr || head->next == nullptr)return head;

2. 拆解问题：前 2 个节点与剩余节点

对于有至少 2 个节点的链表，按以下步骤处理：

步骤 1：定义三个关键节点

• cur：当前链表的第一个节点（需要被交换到第二个位置）；
• next：当前链表的第二个节点（需要被交换到第一个位置，成为新头节点）；
• tail：剩余节点的头（即next->next，需要递归处理的部分，需要考虑为空的特殊情况）。

代码对应：

ListNode* cur = head;         // 第一个节点
ListNode* next = head->next;  // 第二个节点
ListNode* tail = next ? next->next : next;  // 剩余节点的头

步骤 2：交换前 2 个节点

让next成为新的头节点，且next的next指向cur（完成前两个节点的交换）：

next->next = cur;  // 第二个节点指向第一个节点（交换）

步骤 3：递归处理剩余节点，并连接两部分

剩余节点tail的处理结果是一个 “已交换完成的子链表”，需要让cur的next指向这个子链表的头，从而将两部分连接：

cur->next = swapPairs(tail);  // 连接交换后的剩余节点

步骤 4：返回新的头节点

交换后，next成为当前链表的新头节点，因此返回next：

return next;

三、完整代码解析与验证

将上述逻辑整合，得到完整代码：

class Solution {
public:ListNode* swapPairs(ListNode* head) {// 终止条件：节点不足2个，直接返回if(head == nullptr || head->next == nullptr)return head;// 定义三个关键节点ListNode* cur = head;         // 第一个节点ListNode* next = head->next;  // 第二个节点ListNode* tail = next ? next->next : next; // 剩余节点的头// 交换前两个节点next->next = cur;// 递归处理剩余节点，并连接cur->next = swapPairs(tail);// 返回新头节点return next;}
};

验证示例 1：输入1→2→3→4→null

1. 第一层递归：cur=1，next=2，tail=3→4；
   • 交换后2→1；
   • 递归处理tail=3→4，得到返回值4（新头节点）；
   • 1->next = 4，形成2→1→4→3→null；
   • 返回2。
2. 第二层递归（处理3→4）：
   • cur=3，next=4，tail=null；
   • 交换后4→3；
   • 递归处理tail=null，返回null；
   • 3->next = null，形成4→3→null；
   • 返回4。

最终结果为2→1→4→3→null，完全符合预期。

四、总结：递归的核心是 “拆分与连接”

两两交换链表节点的递归解法，本质是将大问题拆成 “前 2 个节点” 和 “剩余节点” 两个子问题：

• 前 2 个节点：直接交换指针，完成局部处理；
• 剩余节点：通过递归复用相同的处理逻辑，得到已交换的子链表；
• 最后将两部分连接，形成完整的交换结果。

这种 “从特殊到一般” 的思考方式，是解决递归问题的通用技巧：先分析最小规模的场景（终止条件），再找到 “拆分问题” 的规律（如何将 n 规模的问题转化为 n-2 规模），最后通过连接子问题的结果得到最终答案。掌握了这种思路，面对复杂的链表操作时，就能化繁为简，轻松应对。