【C++】2025CSP-J第二轮真题及解析

P14357 [CSP-J 2025] 拼数 / number（民间数据）

题目描述

小 R 正在学习字符串处理。小 X 给了小 R 一个字符串 $s$，其中 $s$ 仅包含小写英文字母及数字，且包含至少一个 $1\sim 9$ 中的数字。小 X 希望小 R 使用 $s$ 中的任意多个数字，按任意顺序拼成一个正整数。注意：小 R 可以选择 $s$ 中相同的数字，但每个数字只能使用一次。例如，若 $s$ 为 $1a01b$，则小 R 可以同时选择第 $1,3,4$ 个字符，分别为 $1,0,1$，拼成正整数 $101$ 或 $110$；但小 R 不能拼成正整数 $111$，因为 $s$ 仅包含两个数字 $1$。小 R 想知道，在他所有能拼成的正整数中，最大的是多少。你需要帮助小 R 求出他能拼成的正整数的最大值。

输入格式

输入的第一行包含一个字符串 $s$，表示小 X 给小 R 的字符串。

输出格式

输出一行一个正整数，表示小 R 能拼成的正整数的最大值。

输入输出样例 #1

输入 #1

5

输出 #1

5

输入输出样例 #2

输入 #2

290es1q0

输出 #2

92100

说明/提示

【样例 2 解释】

$s$ 包含数字 $2,9,0,1,0$。可以证明，小 R 拼成的正整数的最大值为 $92100$。

【样例 3】

见选手目录下的 $number/number3.in$ 与 $number/number3.ans$。该样例满足测试点 $9\sim 11$ 的约束条件。

【样例 4】

见选手目录下的 $number/number4.in$ 与 $number/number4.ans$。该样例满足测试点 $20$ 的约束条件。

【数据范围】

设$|s|$为字符串$s$的长度。对于所有测试数据，保证：

• $1\le |s|\le 10^6$；
• $s$仅包含小写英文字母及数字，且包含至少一个$1\sim 9$中的数字。

测试点编号	$s\le$	特殊性质
$1$	$1$	A
$2$	$2$	无
$3$	$2$	无
$4$	$10$	A
$5,6$	$10$	无
$7,8$	$10^2$	A
$9\sim 11$	$10^2$	无
$12$	$10^3$	A
$13,14$	$10^3$	无
$15$	$10^5$	A
$16,17$	$10^5$	B
$18,19$	$10^5$	无
$20$	$10^6$	A
$21,22$	$10^6$	B
$23\sim 25$	$10^6$	无

其中，特殊性质的说明如下：

• 特殊性质A：$s$仅包含数字；
• 特殊性质B：$s$仅包含不超过$10^3$个数字。

算法分析

这道题比较简单，用到桶排序算法。读入时，用string，记录每个0~9的数字，输出时反向输出即可。

完整代码

#include <bits/stdc++.h>
using namespace std;int MAX = 1e6 + 10;string S;
int a[10];int main() {cin >> S;int size = S.size();for (int i = 0; i < size; i++) {int n = S[i] - '0';if (n >= 0 && n <= 9)a[n]++; // 桶}for (int i = 9; i >= 0; i--) {while (a[i] != 0) {a[i]--;cout << i;}}return 0;
}

P14358 [CSP-J 2025] 座位 / seat（民间数据）

题目描述

CSP-J 2025 第二轮正在进行。小 R 所在的考场共有 $n\times m$ 名考生，其中所有考生的 CSP-J 2025 第一轮成绩互不相同。所有 $n\times m$ 名考生将按照 CSP-J 2025 第一轮的成绩，由高到低蛇形分配座位，排列成 $n$ 行 $m$ 列。具体地，设小 R 所在的考场的所有考生的成绩从高到低分别为 $s_1>s_2>\cdots >s_{n\times m}$，则成绩为 $s_1$ 的考生的座位为第 1 列第 $1$ 行，成绩为 $s_2$ 的考生的座位为第 $1$ 列第 $2$ 行，$\dots$，成绩为 $s_n$ 的考生的座位为第 $1$ 列第 $n$ 行，成绩为 $s_{n+1}$ 的考生的座位为第 $2$ 列第 $n$ 行，$\dots$，成绩为 $s_{2n}$ 的考生的座位为第 $2$ 列第 $1$ 行，成绩为 $s_{2n+1}$ 的考生的座位为第 $3$ 列第 $1$ 行，以此类推。

例如，若 $n=4,m=5$，则所有 $4\times 5=20$ 名考生将按照 CSP-J 2025 第一轮成绩从高到低的顺序，根据下图中的箭头顺序分配座位。

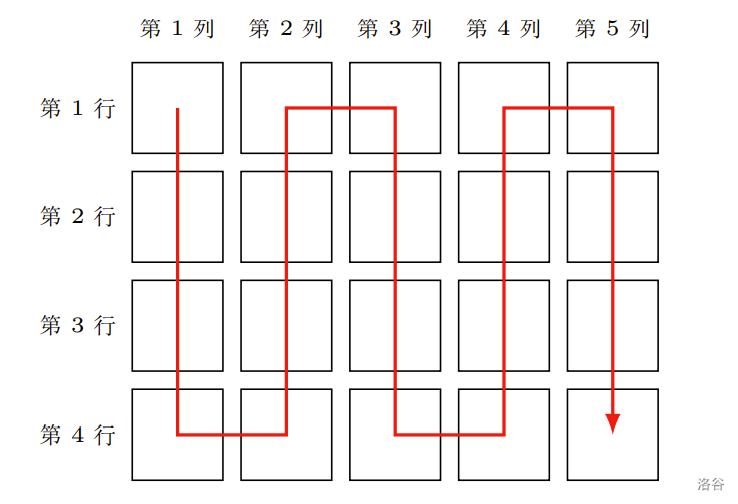
给定小 R 所在的考场座位的行数 $n$ 与列数 $m$，以及小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩 $a_1,a_2,\dots ,a_{n\times m}$，其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩，你需要帮助小 R 求出，他的座位为第几列第几行。

输入格式

输入的第一行包含两个正整数 $n,m$，分别表示小 R 所在的考场座位的行数与列数。

输入的第二行包含 $n\times m$ 个正整数 $a_1,a_2,\dots ,a_{n\times m}$，分别表示小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩，其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩。

输出格式

输出一行两个正整数 $c,r$，表示小 R 的座位为第 $c$ 列第 $r$ 行。

输入输出样例 #1

输入 #1

2 2
99 100 97 98

输出 #1

1 2

输入输出样例 #2

输入 #2

2 2
98 99 100 97

输出 #2

2 2

输入输出样例 #3

输入 #3

3 3
94 95 96 97 98 99 100 93 92

输出 #3

3 1

说明/提示

【样例 1 解释】

按照成绩从高到低的顺序，成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行，成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行，成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行，成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $99$，因此座位为第 $1$ 列第 $2$ 行。

【样例 2 解释】

按照成绩从高到低的顺序，成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行，成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行，成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行，成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $98$，因此座位为第 $2$ 列第 $2$ 行。

【数据范围】

对于所有测试数据，保证：

• $1\le n\le 10$, $1\le m\le 10$;
• 对于所有 $1\le i\le n\times m$，均有 $1\le a_i\le 100$，且 $a_1,a_2,\dots ,a_{n\times m}$ 互不相同。

测试点编号	$n\le$	$m\le$	特殊性质
$1$	$1$	$1$	AB
$2,3$	$1$	$10$	无
$4,5$	$10$	$1$	无
$6$	$2$	$2$	A
$7$	$2$	$2$	B
$8,9$	$2$	$2$	无
$10$	$2$	$10$	A
$11$	$2$	$10$	B
$12\sim 14$	$2$	$10$	无
$15\sim 17$	$10$	$2$	无
$18\sim 20$	$10$	$10$	无

特殊性质 A：对于所有 $1\le i\le n\times m$，均有 $a_i=i$。

特殊性质 B：对于所有 $1\le i\le n\times m$，均有 $a_i=n\times m-i+1$。

算法分析

这题也比较简单（轻轻松松200分~）涉及到的算法为模拟算法。
用sort对分数进行排序后，根据给定的题意进行for循环嵌套即可。

完整代码

#include <bits/stdc++.h>
using namespace std;#define MAXN 1505
int n, m;
int a[MAXN];// 从大到小
bool cmp(int a, int b) { return a > b; }int main() {cin >> n >> m;for (int i = 1; i <= n * m; i++) {cin >> a[i];}const int r = a[1];sort(a + 1, a + n * m + 1, cmp);// for (int i = 1; i <= n * m; i++) {//   cout << a[i] << " ";// }// cout << endl;int idx = 1;for (int j = 1; j <= m; j++) {if (j % 2 != 0) {for (int i = 1; i <= n; i++) {if (a[idx] == r) {cout << j << " " << i;}idx++;}} else {for (int i = n; i >= 1; i--) {if (a[idx] == r) {cout << j << " " << i;}idx++;}}}return 0;
}

P14359 [CSP-J 2025] 异或和 / xor（民间数据）

题目描述

小 R 有一个长度为 $n$ 的非负整数序列 $a_1,a_2,\dots ,a_n$。定义一个区间 $[l,r]$ ($1\le l\le r\le n$) 的权值为 $a_l,a_{l+1},\dots ,a_r$ 的二进制按位异或和，即 $a_l\oplus a_{l+1}\oplus \cdots \oplus a_r$，其中 $\oplus$ 表示二进制按位异或。

小 X 给了小 R 一个非负整数 $k$。小 X 希望小 R 选择序列中尽可能多的不相交的区间，使得每个区间的权值均为 $k$。两个区间 $[l_1,r_1],[l_2,r_2]$ 相交当且仅当两个区间同时包含至少一个相同的下标，即存在 $1\le i\le n$ 使得 $l_1\le i\le r_1$ 且 $l_2\le i\le r_2$。

例如，对于序列 $[2,1,0,3]$，若 $k=2$，则小 R 可以选择区间 $[1,1]$ 和区间 $[2,4]$，权值分别为 $2$ 和 $1\oplus 0\oplus 3=2$；若 $k=3$，则小 R 可以选择区间 $[1,2]$ 和区间 $[4,4]$，权值分别为 $1\oplus 2=3$ 和 $3$。

你需要帮助小 R 求出他能选出的区间数量的最大值。

输入格式

输入的第一行包含两个非负整数 $n,k$，分别表示小 R 的序列长度和小 X 给小 R 的非负整数。

输入的第二行包含 $n$ 个非负整数 $a_1,a_2,\dots ,a_n$，表示小 R 的序列。

输出格式

输出一行一个非负整数，表示小 R 能选出的区间数量的最大值。

输入输出样例 #1

输入 #1

4 2
2 1 0 3

输出 #1

2

输入输出样例 #2

输入 #2

4 3
2 1 0 3

输出 #2

2

输入输出样例 #3

输入 #3

4 0
2 1 0 3

输出 #3

1

说明/提示

【样例 1 解释】

小 R 可以选择区间 $[1,1]$ 和区间 $[2,4]$，异或和分别为 $2$ 和 $1\oplus 0\oplus 3=2$。可以证明，小 R 能选出的区间数量的最大值为 $2$。

【样例 2 解释】

小 R 可以选择区间 $[1,2]$ 和区间 $[4,4]$，异或和分别为 $1\oplus 2=3$ 和 $3$。可以证明，小 R 能选出的区间数量的最大值为 $2$。

【样例 3 解释】

小 R 可以选择区间 $[3,3]$，异或和为 $0$。可以证明，小 R 能选出的区间数量的最大值为 $1$。注意：小 R 不能同时选择区间 $[3,3]$ 和区间 $[1,4]$，因为这两个区间同时包含下标 $3$。

【样例 4】

见选手目录下的 $xor/xor4.in$ 与 $xor/xor4.ans$。

该样例满足测试点 $4,5$ 的约束条件。

【样例 5】

见选手目录下的 $xor/xor5.in$ 与 $xor/xor5.ans$。

该样例满足测试点 $9,10$ 的约束条件。

【样例 6】

见选手目录下的 $xor/xor6.in$ 与 $xor/xor6.ans$。

该样例满足测试点 $14,15$ 的约束条件。

【数据范围】

对于所有测试数据，保证：

• $1\le n\le 5\times 10^5$，$0\le k<2^{20}$；
• 对于所有 $1\le i\le n$，均有 $0\le a_i<2^{20}$。

测试点编号	$n\le$	$k$ 范围	特殊性质
$1$	$2$	$=0$	A
$2$	$10$	$\le 1$	B
$3$	$10^2$	$=0$	A
$4,5$	$10^2$	$\le 1$	B
$6\sim 8$	$10^2$	$\le 255$	C
$9,10$	$10^3$	$<2^{20}$	无
$11,12$	$10^3$	$<2^{20}$	无
$13$	$2\times 10^5$	$\le 1$	B
$14,15$	$2\times 10^5$	$\le 255$	C
$16$	$2\times 10^5$	$<2^{20}$	无
$17$	$5\times 10^5$	$\le 255$	C
$18\sim 20$	$5\times 10^5$	$<2^{20}$	无

其中，特殊性质的说明如下：

• 特殊性质A：对于所有 $1\le i\le n$，均有 $a_i=1$；
• 特殊性质B：对于所有 $1\le i\le n$，均有 $0\le a_i\le 1$；
• 特殊性质C：对于所有 $1\le i\le n$，均有 $0\le a_i\le 255$。

算法分析

1. 求异或的代码为a=b^c，如果这个忘了就基本凉凉了~
2. 这题用到的算法是dp，定义 dp[i] 表示前$i$个元素中能选出的最大不相交区间数量。
3. 对于每个位置$i$，有两种选择：
   • 不选第 $i$个元素作为区间终点：此时 dp[i] = dp[i-1]
   • 选第$i$个元素作为区间终点：需找到以$i$结尾且异或和为$k$的区间 $[j+1,i]$，则 dp[i] = max(dp[i], dp[j] + 1)
4. 至此，算法逻辑写完可以拿60分，接下来是优化。
   • 在反向查找时添加一个break，因为找到一个区间，后面的区间长度不会超过当前的区间长度。（这个可以拿80分）
   • 记录上一个区间的结束位置，定义一个 last 变量记录上一个选中区间的结束位置，确保区间不相交，只需要检查j >= last的范围。（至此，已拿满分）

完整代码

#include <bits/stdc++.h>
using namespace std;#define int long long
const int MAXN = 1e5 * 5 + 10;int n, k;
int a[MAXN], dp[MAXN];signed main() {cin >> n >> k;for (int i = 1; i <= n; i++) {cin >> a[i];}dp[0] = 0;int last = 0; // 记录上一个区间的结束位置for (int i = 1; i <= n; i++) {dp[i] = dp[i - 1];int s = a[i];for (int j = i - 1; j >= last; j--) {if (s == k) { // 找到可能的区间dp[i] = max(dp[i], dp[j] + 1);last = j; // 更新上一个区间的结束位置break; // 找到一个区间，后面的区间长度不会超过当前的区间长度}s = s ^ a[j]; // 求异或和}}cout << dp[n] << endl;return 0;
}

P14360 [CSP-J 2025] 多边形 / polygon（民间数据）

题目描述

小 R 喜欢玩小木棍。小 R 有 $n$ 根小木棍，第 $i$ ($1\le i\le n$) 根小木棍的长度为 $a_i$。

小 X 希望小 R 从这 $n$ 根小木棍中选出若干根小木棍，将它们按任意顺序首尾相连拼成一个多边形。小 R 并不知道小木棍能拼成多边形的条件，于是小 X 直接将条件告诉了他：对于长度分别为 $l_1,l_2,\dots ,l_m$ 的 $m$ 根小木棍，这 $m$ 根小木棍能拼成一个多边形当且仅当 $m\ge 3$ 且所有小木棍的长度之和大于所有小木棍的长度最大值的两倍，即 ${\sum }_{i=1}^m{l}_i>2\times {\max }_{i=1}^m{l}_i$。

由于小 R 知道了小木棍能拼成多边形的条件，小 X 提出了一个更难的问题：有多少种选择小木棍的方案，使得选出的小木棍能够拼成一个多边形？你需要帮助小 R 求出选出的小木棍能够拼成一个多边形的方案数。两种方案不同当且仅当选择的小木棍的下标集合不同，即存在 $1\le i\le n$，使得其中一种方案选择了第 $i$ 根小木棍，但另一种方案未选择。由于答案可能较大，你只需要求出答案对 $998,244,353$ 取模后的结果。

输入格式

输入的第一行包含一个正整数 $n$，表示小 R 的小木棍的数量。

输入的第二行包含 $n$ 个正整数 $a_1,a_2,\dots ,a_n$，表示小 R 的小木棍的长度。

输出格式

输出一行一个非负整数，表示小 R 选出的小木棍能够拼成一个多边形的方案数对 $998,244,353$ 取模后的结果。

输入输出样例 #1

输入 #1

5
1 2 3 4 5

输出 #1

9

输入输出样例 #2

输入 #2

5
2 2 3 8 10

输出 #2

6

说明/提示

【样例 1 解释】

共有以下 $9$ 种选择小木棍的方案，使得选出的小木棍能够拼成一个多边形：

1. 选择第 $2,3,4$ 根小木棍，长度之和为 $2+3+4=9$，长度最大值为 $4$;
2. 选择第 $2,4,5$ 根小木棍，长度之和为 $2+4+5=11$，长度最大值为 $5$;
3. 选择第 $3,4,5$ 根小木棍，长度之和为 $3+4+5=12$，长度最大值为 $5$;
4. 选择第 $1,2,3,4$ 根小木棍，长度之和为 $1+2+3+4=10$，长度最大值为 $4$;
5. 选择第 $1,2,3,5$ 根小木棍，长度之和为 $1+2+3+5=11$，长度最大值为 $5$;
6. 选择第 $1,2,4,5$ 根小木棍，长度之和为 $1+2+4+5=12$，长度最大值为 $5$;
7. 选择第 $1,3,4,5$ 根小木棍，长度之和为 $1+3+4+5=13$，长度最大值为 $5$;
8. 选择第 $2,3,4,5$ 根小木棍，长度之和为 $2+3+4+5=14$，长度最大值为 $5$;
9. 选择第 $1,2,3,4,5$ 根小木棍，长度之和为 $1+2+3+4+5=15$，长度最大值为 $5$。

【样例 2 解释】

共有以下 $6$ 种选择小木棍的方案，使得选出的小木棍能够拼成一个多边形：

1. 选择第 $1,2,3$ 根小木棍，长度之和为 $2+2+3=7$，长度最大值为 $3$;
2. 选择第 $3,4,5$ 根小木棍，长度之和为 $3+8+10=21$，长度最大值为 $10$;
3. 选择第 $1,2,4,5$ 根小木棍，长度之和为 $2+2+8+10=22$，长度最大值为 $10$;
4. 选择第 $1,3,4,5$ 根小木棍，长度之和为 $2+3+8+10=23$，长度最大值为 $10$;
5. 选择第 $2,3,4,5$ 根小木棍，长度之和为 $2+3+8+10=23$，长度最大值为 $10$;
6. 选择第 $1,2,3,4,5$ 根小木棍，长度之和为 $2+2+3+8+10=25$，长度最大值为 $10$。

【样例 3】

见选手目录下的 $polygon/polygon3.in$ 与 $polygon/polygon3.ans$。

该样例满足测试点 $7\sim 10$ 的约束条件。

【样例 4】

见选手目录下的 $polygon/polygon4.in$ 与 $polygon/polygon4.ans$。

该样例满足测试点 $11\sim 14$ 的约束条件。

【子任务】

对于所有测试数据，保证：

• $3\le n\le 5000$；
• 对于所有 $1\le i\le n$，均有 $1\le a_i\le 5000$。

测试点编号	$n\le$	${\max }_{i=1}^n{a}_i\le$
$1\sim 3$	$3$	$10$
$4\sim 6$	$10$	$10^2$
$7\sim 10$	$20$	$10^2$
$11\sim 14$	$500$	$10^2$
$15\sim 17$	$500$	$1$
$18\sim 20$	$5000$	$1$
$21\sim 25$	$5000$	$5000$

算法分析

1. 观察后发现，总方案数好求（就是$2^n$），然后我们求得不满足条件的方案数，拿总方案数去减更方便。本题采用动态规划算法。
   • 定义一个三维数组dp，其中三个维度分别为：
     • 第一个维度 i：表示考虑前 i 个数，即处理到数组的第 i 个元素。
     • 第二个维度 j：表示当前选择的元素的总和为 j。
     • 第三个维度 k（取值为0、1、2）：表示在考虑前 i 个数且总和为 j 的情况下，当前选择的元素个数状态：
       • k=0：表示一个元素都没有选。
       • k=1：表示恰好选择了1个元素。
       • k=2：表示选择了2个或2个以上的元素。
   • 状态转移：
     • 不选当前元素：继承上一层状态。
     • 选当前元素：根据已有选中数量更新状态
     • 当选择当前元素且满足j >= a[i]（即当前总和j能容纳该元素值）时：
       • dp[i][j][1]的更新：在之前未选中任何元素（k=0）的状态下，选择当前元素后，选中数量变为1（k=1），因此加上dp[i-1][j - a[i]][0]。
       • dp[i][j][2]的更新：在之前已选中1个元素（k=1）或已选中2个及以上元素（k=2）的状态下，选择当前元素后，选中数量变为2个及以上（k=2），因此加上dp[i-1][j - a[i]][1] + dp[i-1][j - a[i]][2]。
     • 代码如下所示。

if (j >= a[i]) {dp[i][j][1] = (dp[i][j][1] + dp[i - 1][j - a[i]][0]) % MOD;dp[i][j][2] = (1ll * dp[i][j][2] + dp[i - 1][j - a[i]][1] + dp[i - 1][j - a[i]][2]) % MOD;
}

2. 前缀和优化：用sum[cur][j]记录前j个和的状态2的累加和，快速计算不满足条件的子集数量。

• 在处理第i个元素、总和为j的状态时，通过前缀和sum[i][j]累加前j个总和中状态为k=2（即选择了2个及以上元素）的方案数。sum[i][j]的值由前一项sum[i][j-1]加上当前的dp[i][j][2]得到，实现了对状态2的累加和记录，从而可以快速计算相关的子集数量。
• 前缀和优化中用于记录前j个和的状态2累加和的代码如下所示。

// 维护sum
sum[i][j] = (sum[i][j - 1] + dp[i][j][2]) % MOD;

3. 结果计算：
   • 对每个元素a[i]（排序后作为最大值），总方案数为$2^{i-1}$（前i个元素的非空子集）
   • 减去无效方案即为答案。无效方案包括：大小为1的子集、大小≥3但不满足和的条件的子集。
   • 代码逻辑说明如下
     • mi[i - 1]：对应“总方案数为$2^{i-1}$”，mi数组提前存储了2的幂次（mi[k] = 2^k mod MOD），前i个元素的非空子集数为$2^{i-1}$。
     • - i：对应“减去大小为1的子集”，前i个元素中大小为1的子集共i个（每个元素单独作为子集）。
     • - sum[i - 1][a[i]]：对应“减去大小≥3但不满足和的条件的子集”，sum[i-1][a[i]]是前i-1个元素中“和≤a[i]且选中2个及以上元素”的方案数（这些方案加上a[i]后，总和≤2×a[i]，不满足多边形条件）。
     • 整体累加并取模：将每个以a[i]为最大值的有效方案数累加，得到最终答案。

int ans = 0;
for (int i = 3; i <= n; i++) {ans = ((ans + mi[i - 1] - i - sum[i - 1][a[i]]) % MOD + MOD) % MOD;
}

4. 用滚动数组优化，不然会MLE只有68分。dp数组的第一个维度用一个变量cur来滚动使用。
   • dp[cur][j][s]，其中cur为滚动数组当前层，j为元素和，s为状态。

完整代码

没有用滚动数组优化的原始版本：

#include <bits/stdc++.h>
using namespace std;#define int long long
const int MAXN = 5001;
const int MOD = 998244353;
int n, aMax;
// 前i个数里总和为j的方案数，k为选择的个数，k=2为选了2个以上
int a[MAXN], dp[MAXN][MAXN][3], sum[MAXN][MAXN];
int mi[MAXN];signed main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];aMax = max(aMax, a[i]);}sort(a + 1, a + n + 1);// 初始化2的幂mi[0] = 1;for (int i = 1; i <= MAXN; i++) {mi[i] = mi[i - 1] * 2 % MOD;}dp[0][0][0] = 1;for (int i = 1; i <= n; i++) {dp[i][0][0] = 1;for (int j = 1; j <= aMax; j++) {// 不选dp[i][j][1] = dp[i - 1][j][1];dp[i][j][2] = dp[i - 1][j][2];// 选if (j >= a[i]) {dp[i][j][1] = (dp[i][j][1] + dp[i - 1][j - a[i]][0]) % MOD;dp[i][j][2] = (1ll * dp[i][j][2] + dp[i - 1][j - a[i]][1] + dp[i - 1][j - a[i]][2]) % MOD;}// 维护sumsum[i][j] = (sum[i][j - 1] + dp[i][j][2]) % MOD;}}int ans = 0;for (int i = 3; i <= n; i++) {ans = ((ans + mi[i - 1] - i - sum[i - 1][a[i]]) % MOD + MOD) % MOD;}cout << ans << endl;return 0;
}

用滚动数组优化后的版本如下。

#include <bits/stdc++.h>
using namespace std;#define int long long
const int MAXN = 5001;
const int MOD = 998244353;
int n, aMax;
int a[MAXN];
int dp[2][MAXN][3]; // 使用滚动数组，只保留当前层和上一层
int sum[2][MAXN];   // 滚动数组优化sum
int mi[MAXN];signed main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];aMax = max(aMax, a[i]);}sort(a + 1, a + n + 1);// 初始化2的幂mi[0] = 1;for (int i = 1; i <= MAXN; i++) {mi[i] = mi[i - 1] * 2 % MOD;}// 初始化dp数组int cur = 0;memset(dp[cur], 0, sizeof(dp[cur]));dp[cur][0][0] = 1;// 初始化sum数组memset(sum, 0, sizeof(sum));int ans = 0;for (int i = 1; i <= n; i++) {cur ^= 1; // 切换当前层// 先清空当前层，然后复制不选的情况memset(dp[cur], 0, sizeof(dp[cur]));dp[cur][0][0] = 1; // 不选任何元素的情况// 复制上一层的状态作为不选当前元素的情况for (int j = 0; j <= aMax; j++) {dp[cur][j][1] = dp[cur ^ 1][j][1];dp[cur][j][2] = dp[cur ^ 1][j][2];}// 处理选当前元素的情况for (int j = a[i]; j <= aMax; j++) {// 选当前元素，且这是第一个选中的元素dp[cur][j][1] = (dp[cur][j][1] + dp[cur ^ 1][j - a[i]][0]) % MOD;// 选当前元素，且这是第二个或更多选中的元素dp[cur][j][2] = (dp[cur][j][2] + dp[cur ^ 1][j - a[i]][1] + dp[cur ^ 1][j - a[i]][2]) % MOD;}// 维护前缀和sum[cur][j] = sum_{k=0}^j dp[cur][k][2]sum[cur][0] = 0;for (int j = 1; j <= aMax; j++) {sum[cur][j] = (sum[cur][j - 1] + dp[cur][j][2]) % MOD;}// 计算以a[i]为最大值时的有效方案数// 注意：这里使用current层，对应原代码中的i层if (i >= 3) {// 总共有mi[i-1]种方式选择前i个元素中的非空子集// 减去只选一个元素的i种方式// 减去选三个或更多元素但不满足条件的情况（即sum[cur][a[i]]）ans = ((ans + mi[i-1] - i - sum[cur][a[i]]) % MOD + MOD) % MOD;}}cout << ans << endl;return 0;
}