C++信息学奥赛 递推-动态规划 数塔与过河卒模型实战解析 图例+详解+状态转移方程
数塔
一、数塔问题模型
下图是一个数字三角形,现在想要找到从顶端到底端的某处的一条路径,使得路径所经过的数字总和最大。
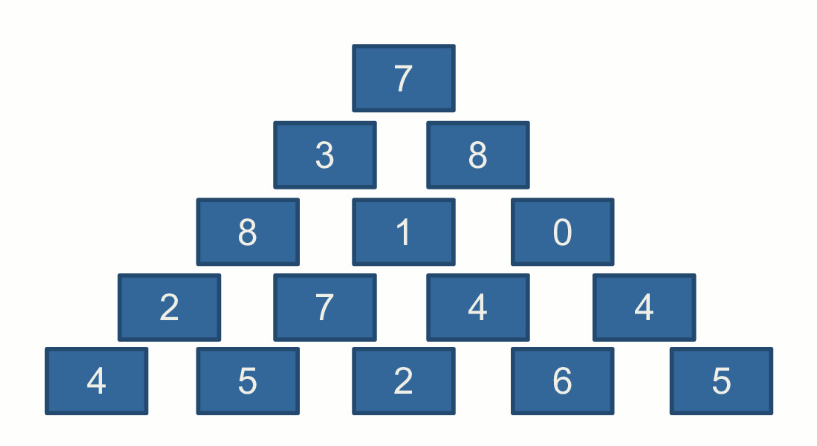
可以发现任何一个位置,要么从其左上方到达,要么从其右上方到达。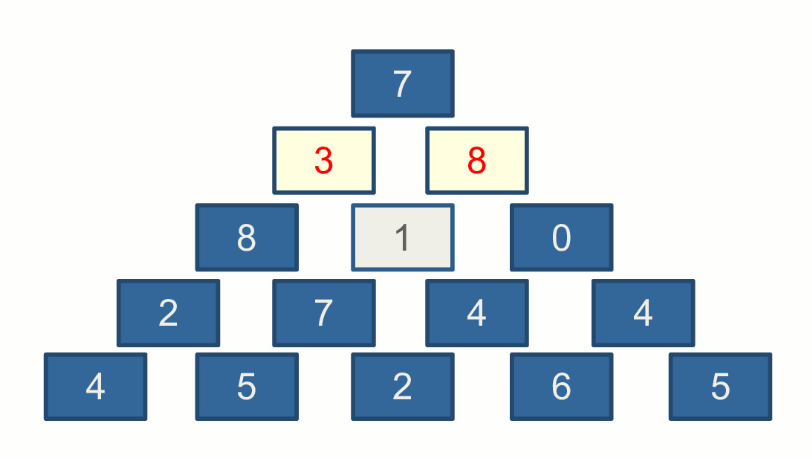
【问题解法】
如果从其左上方到达,那么这个点能取到的数字之和的最大值等于,从顶端到其左上方的点能得到的数字之和的最大值加上当前位置的值。
如果从其右上方到达,那么这个点能取到的数字之和的最大值等于,从顶端到其右上方的点能得到的数字之和的最大值加上当前位置的值。
最后当前位置应从左上方和右上方各自的从顶端到当前位置的最大值中再取一个最大值。
二、求解过程
- 递推项(状态)
我们可以用一个二维数组a去存储数字三角形。可以发现任一位置a[i][j],其左上为a[i-1][j-1],其右上为a[i-1][j] - 目标
我们定义一个二维数组f。其中f[i][j]用来存储从数字三角形顶端到第i行第j列能取到数字之和的最大值。
那么答案应该是从顶端到底端,也就是第n行某列上能取
到的数字之和的最大值,即max{f[n][j]}, 1<=j<=n。 - 递推式
经过刚才的分析,我们可以确定,第i行第j列能取到的最大值要么从左上方过来得到,则此时f[i][j]=f[i-1][j-1]+a[i][j];
要么从右上方过来得到,则此时f[i][j]=f[i-1][j]+a[i][j];
最后f[i][j]要从左上方过来和右.上方过来中取一个最大值,f[i][j]=max(f[i-1][j-1]+a[i][j], f[i-1][j]+a[i][j])。 - 边界
最上方的一个元素,就是递推的边界f[1][1]=a[1][1]
三、递推算法
递推算法的首要问题是得到相邻的数据项之间的关系(即
递推关系)
递推算法避开了求通项公式的麻烦,把一个复杂的问题的求解,分解成了连续的若干步简单运算。
状态: f[i][j]表示从顶部走到(,j)的最优解。
递推式: f[i][i]=max(f[i-1][j-1]+a[i]i], f[i-1][j]+a[i][i])
边界:f[1][1]=a[1][1]
目标: max([n][j]),1<=j<=n
四、另一种解法
数塔问题还可以自底向上递推。
状态:定义f[i][j]表示从数塔底端某个位置到第i行第j列的最大值。
递推式: 第i行第j列能取到的最大值要么从左下方过来得到,要么从右下方过来得到。
f[i][j]=max(f[i+1][j]+a[i][j], f[i+1][j+1]+a[i][j])
边界: f[n][i]=a[n][i],
1<=i<=n
目标:f[1][1]五、例题选讲
【3164 数字金字塔】
3164 数字金字塔
经验值:800
时间限制:1000毫秒
内存限制:128MB
题目描述 Description
观察下面的数字金字塔。从金字塔的顶部斜向下走,每一步可以走到左下方或右下方的一个点。请编写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。73 88 1 0 2 7 4 4 4 5 2 6 5
在上图的样例中,路径7->3->8->7->5 的数字之和最大。输入描述 Input Description
第一个行有一个整数R(1≤R≤1000) ,表示金字塔的层数。接下来有R行,其中的第i行有i个整数,用空格隔开,表示从金字塔塔顶开始的第i行内从左向右的所有整数。金字塔上所有的整数都是不大于100的非负整数。输出描述 Output Description
一个整数,表示可得到的最大的和。样例输入 Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出 Sample Output
30
【方法1】#include<iostream>
using namespace std;
int n,a[1005][1005];
int f[1005][1005];//f[i][j]:从顶端到第i行第j列位置的最大路径之和
int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}f[1][1]=a[1][1];//边界for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){if(j==1){//第1列,只能从上面过来f[i][j]=f[i-1][j]+a[i][j];}else if(j==i){//第i列,只能从左上方过来f[i][j]=f[i-1][j-1]+a[i][j];}else{f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];}}}
// for(int i=1;i<=n;i++){
// for(int j=1;j<=i;j++){
// cout<<f[i][j]<<" ";
// }
// cout<<endl;
// }//找第n层,所有最大路径和中的最大值int ans=-0x3f3f3f3f;for(int i=1;i<=n;i++){ans=max(ans,f[n][i]);}cout<<ans;return 0;
}
【方法2】#include<iostream>
using namespace std;
int n,a[1005][1005];
int f[1005][1005];//f[i][j]:从顶端到第i行第j列位置的最大路径之和
int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}for(int i=n;i>=1;i--){for(int j=1;j<=i;j++){if(i==n){//第n行f[i][j]=a[i][j];}else{f[i][j]=max(f[i+1][j+1],f[i+1][j])+a[i][j];}}}
// for(int i=1;i<=n;i++){
// for(int j=1;j<=i;j++){
// cout<<f[i][j]<<" ";
// }
// cout<<endl;
// }cout<<f[1][1];return 0;
}【4399 走迷宫】
4399 走迷宫
经验值:800
时间限制:1000毫秒
内存限制:128MB
题目描述 Description
小P被困在了如下图所示的一个数字三角形迷宫里,每一条路都用一个数字表示。
现规定从最顶层走到最底层,每一步可沿左斜线向下或右斜线向下走。其中规定,假设三角形行数 n≤100,小P必须经过迷宫中的某一位置,使之走的所有路上数字之和最大。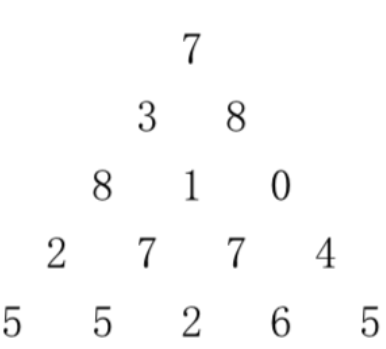
输入描述 Input Description
n+1行,第一行三个数字n,x,y,分别表示三角形迷宫的行数、必须经过的路的坐标
下面n行,分别代表三角形迷宫每条路上的数字输出描述 Output Description
一个整数,表示小P所走路径的数字之和最大值样例输入 Sample Input
3 2 2
1
2 3
4 5 6
样例输出 Sample Output
10
数据范围及提示 Data Size & Hint
1<=n<=100,数塔中每个数字是不超过10的正整数
#include<iostream>
using namespace std;
int a[105][105],f[105][105];
int n,x,y;
int maxn=-1;
int main(){cin>>n>>x>>y;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}a[x][y]+=0x3f3f3f3f;f[1][1]=a[1][1];for(int i=2;i<=n;i++){//行数for(int j=1;j<=i;j++){f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);}}for(int j=1;j<=n;j++){//遍历最后一行,找最大值maxn=max(f[n][j],maxn);}cout<<maxn-0x3f3f3f3f;return 0;
}
过河卒
一、过河卒问题模型
棋盘_上A点有一个过河卒,需要走到B点。假设棋盘的大小是m行n列。
卒行走的规则:可以向下或者向右。同时棋盘上C点有一个马,该马所在的点,以及跳一步可达的点称为马的控制点。卒不能经过马的控制点。现在求卒从点A到点B的路径的方案数。
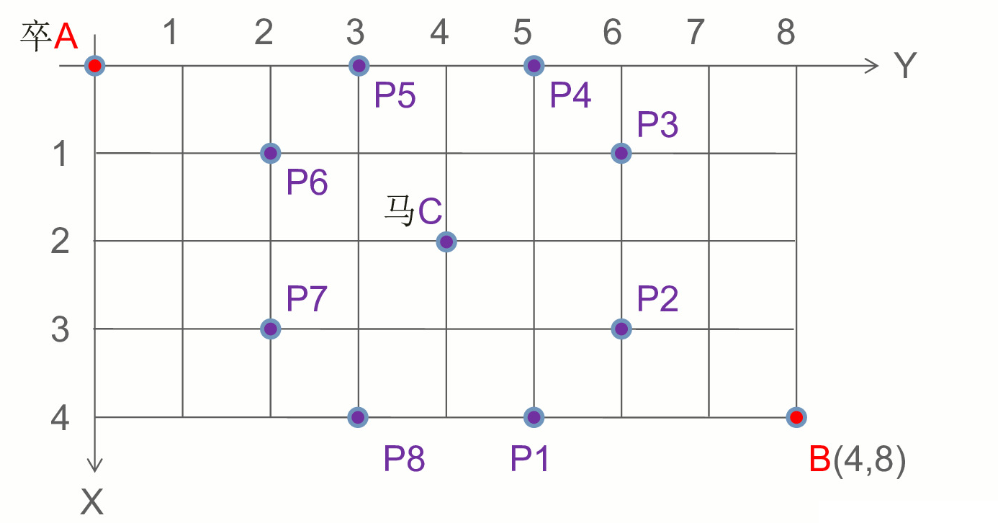
首先x==0的点和y==0的点,分别只能通过一直向下和一直向右走到。
所以这些点的方案数均为1。直到遇到第一-个控制点后,方案数均变为0。
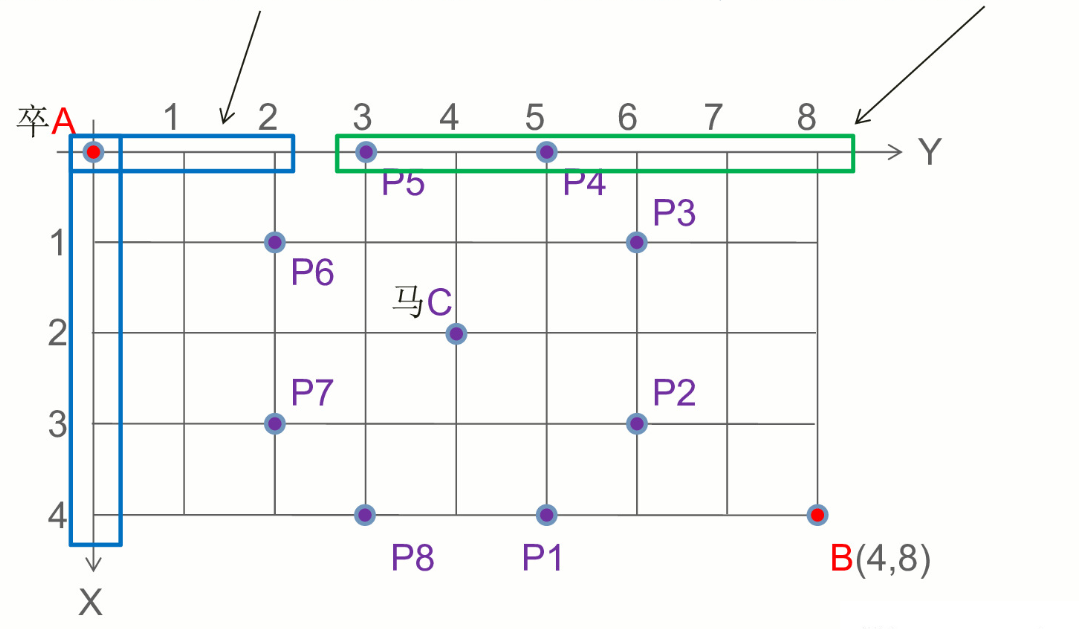
其余各点,如果是控制点,则一定不可达,这些点到达的方案数为0;其它点要么从左边,要么从上边过来,所以这些点的方案数为左边的点到达的方案数加上,上边的点到达的方案数。
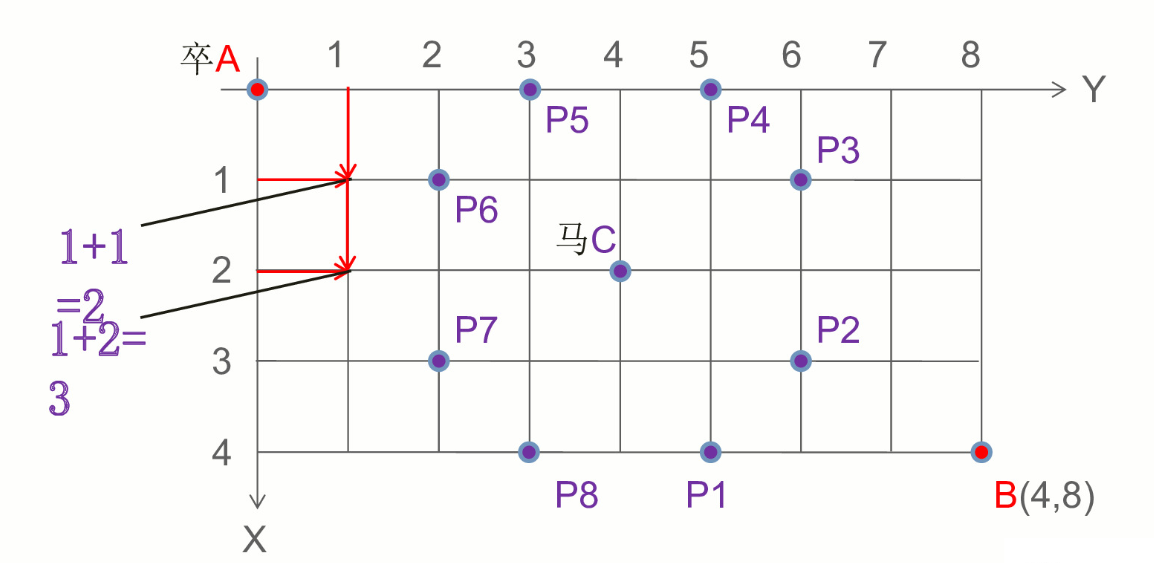
1.状态
首先我们可以定义状态为一个二维数组f[i][j],表示走到第i行第j列的方案数。
由于在计算一个位置能到达的方案数时,要用到到达其上方和左方的方案数。所以我们在递推的时候需要按照从上往下,从左往右的顺序进行递推。
每个点是否为控制点的信息可以用一个额外的二维数组来存储。
2.边界
是否为控制点我们可以用一个二维数组t[i][j]表示.
t[i][j]==0表示不是控制点,
t[i][j]==1表示是控制点。
3.状态转移方程
if(t[i][j]==1){//是控制点 continue; } if(i-1>=0){//没有越界 f[i][j]+=f[i-1][j];//把上一行的方案数加过来 } if(j-1>=0){//没有越界 f[i][j]+=f[i][j-1];//把左边的方案数加过来 } 二、课堂练习选讲
4391 过河卒
4391 过河卒
经验值:1200
时间限制:1000毫秒
内存限制:128MB
题目描述 Description
棋盘上A点有一个过河卒,需要走到目标B点。卒的行走规则:可以向下或者向右。同时在棋盘上的某一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点成为对方马的控制点,如图中的C的和 P1 ~ P8,卒不能通过对方马的控制点。棋盘用坐标表示,A(0,0)、B(n,m),同样马的位置坐标是需要给出的,C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径条数。
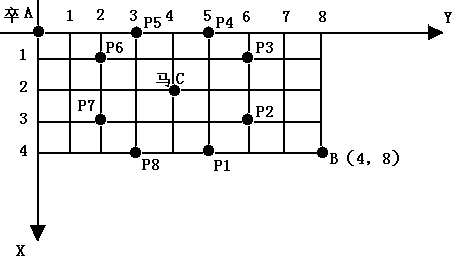
输入描述 Input Description
给出n、m和C点的坐标输出描述 Output Description
从A点能够到达B点的路径的条数样例输入 Sample Input
8 6 0 4
样例输出 Sample Output
1617
数据范围及提示 Data Size & Hint
0<=m,n<=20
/*
起点:A(0,0)
终点:B(n,m)
每一步只能往下 或者 往右控制点:马和马一步可达的位置
马不在起点或者终点,但控制点可能在求:从A点到B点的方案数读入:n m马的坐标不考虑马的过河卒问题1、数组含义(状态)f[i][j]:从(0,0)走到(i,j)的方案数2、递推关系如果(i,j)是控制点 continue当前在(i,j),上一步只有可能在(i-1,j)或者(i,j-1)if(i-1>=0){f[i][j]+=f[i-1][j];//将上面的方案加进来}if(j-1>=0){f[i][j]+=f[i][j-1];//将左边的方案加进来}3、边界如果起点不是控制点 f[0][0]=1 起点到起点的方案数是14、解f[n][m]准备工作:用二维的桶数组,对每个点是不是控制点做标记原理:控制点 - 马的坐标 = 差计算的:行差 列差-2 1-1 21 22 12 -11 -2-1 -2-2 -1反之:控制点 = 马的坐标 + 差
*/
#include<iostream>
using namespace std;
int f[25][25];//f[i][j]:从(0,0)走到(i,j)的方案数
bool t[25][25];//标记是否是控制点
int dir[9][3]={{0,0},{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2},{-2,-1}};
int n,m,x,y;
int main(){cin>>n>>m>>x>>y;//标记控制点for(int i=0;i<=8;i++){int nx=dir[i][0]+x;int ny=dir[i][1]+y;if(nx>=0&&nx<=n&&ny>=0&&ny<=m){t[nx][ny]=true;//标记控制点}}if(t[0][0]!=1){f[0][0]=1;}for(int i=0;i<=n;i++){for(int j=0;j<=m;j++){if(t[i][j]==1){//是控制点continue;}if(i-1>=0){f[i][j]+=f[i-1][j];//将上面的方案加进来}if(j-1>=0){f[i][j]+=f[i][j-1];//将左边的方案加进来}}}cout<<f[n][m];return 0;
}4507 马走棋盘
4507 马走棋盘
经验值:1600
时间限制:1000毫秒
内存限制:128MB
题目描述 Description
现在有一个大小为m * n的棋盘,棋盘的左上角(0,0)有一个象棋棋子——马(马在象棋中,只能走“日”),棋盘上另一个位置(x,y)有一个敌方的车。现在马想从棋盘的左上角走到棋盘的右下角(m,n),但是不能落在车的同一行或者同一列(会被车吃掉),且马只能往右走不能往左走。请你编写一个程序,计算马有多少种不同的路径到达棋盘的右下角。输入描述 Input Description
两行,第一行两个整数m、n、x、y,分别表示棋盘的行、列和车所在的行、列输出描述 Output Description
一个整数,表示共有多少种不同的路径样例输入 Sample Input
7 7 4 4
样例输出 Sample Output
1
数据范围及提示 Data Size & Hint
2<=m, n<=20
2<=x<=m
2<=y<=n
/*
4507 马走棋盘左上角有一个马,走到右下角马每次只能朝着右下方前进有一个控制点车,所在行和所在列都不能走1、状态f[i][j]:从(0,0)到(i,j)的方案数2、递推关系(只能往右)if(i==x||j==y){continue;}ifi+2<=n&&j-1>=0){f[i][j]+=f[i+2][j-1];}if(i+1<=n&&j-2>=0){f[i][j]+=f[i+1][j-2];}if(i-2>=0&&j-1>=0){f[i][j]+=f[i-2][j-1];}if(i-1>=0&&j-2>=0){f[i][j]+=f[i-1][j-2];}3、边界if(x!=0&&y!=0){f[0][0]=1;}4、解 f[n][m]
*/
#include<iostream>
using namespace std;
int f[35][35];
int m,n,x,y;
int main(){cin>>m>>n>>x>>y;//边界if(x==0||y==0){f[0][0]=0;}else{f[0][0]=1;}//必须要先遍历列再遍历行,否则的话左下方的点到达不了for(int j=0;j<=n;j++){for(int i=0;i<=m;i++){//不能走车所在的行和列if(i==x||j==y){continue;}//防止越界if(i+1<=m&&j-2>=0){f[i][j]+=f[i+1][j-2];}if(i+2<=m&&j-1>=0){f[i][j]+=f[i+2][j-1];}if(i-1>=0&&j-2>=0){f[i][j]+=f[i-1][j-2];}if(i-2>=0&&j-1>=0){f[i][j]+=f[i-2][j-1];}}}cout<<f[m][n];return 0;
}
5102 过河车
5102 过河车
经验值:1600
时间限制:1000毫秒
内存限制:128MB
题目描述 Description
小卒在过河的过程中遇到了马的围追堵截,艰难的来到了终点。现在他的老大,车也打算过河。在一个n×m的棋盘上,左上角(0,0)处有一只象棋中的车。在某个位置(x,y)处有一个马。现在车朝着右下角(n,m)位置前进,但是前进的过程中不能走到马所在的点,以及马控制的那些位置。并且车每次只能朝着右方或下方前进。试求出车有多少种方案到达右下角。输入描述 Input Description
一行,四个空格隔开的整数,n m x y输出描述 Output Description
车到达右下角的方案数样例输入 Sample Input
8 6 0 4
样例输出 Sample Output
266962
数据范围及提示 Data Size & Hint
0<=m,n<=10
#include<iostream>
using namespace std;
int n,m,x,y;
int f[15][15];
bool b[15][15];
int dir[9][2]={{0,0},{2,1},{-2,-1},{-2,1},{2,-1},{1,2},{-1,-2},{1,-2},{-1,2}};//方向
int main(){cin>>n>>m>>x>>y;//控制点for(int i=0;i<9;i++){int nx=x+dir[i][0];int ny=y+dir[i][1];b[nx][ny]=true;}//边界if(!b[0][0]){f[0][0]=1;}for(int i=0;i<=n;i++){for(int j=0;j<=m;j++){if(b[i][j]==true){continue;}//车可以向下或者向右走一条线for(int k=0;k<i;k++){f[i][j]+=f[k][j];}for(int k=0;k<j;k++){f[i][j]+=f[i][k];}}}cout<<f[n][m];return 0;
}