当前位置：首页 > news >正文

动态规划的解题套路1-泰波那契模型

news 2025/11/3 8:57:59

文章目录

一、dp问题的通用思路
二.第N个泰波那契数
- 3.1 解题思路：
- 3.2 代码:
三. 三步问题
- 4.1 解题思路：
- 4.2 代码：
四.使用最小花费爬楼梯
- 4.1 解题思路：
- 4.2 代码：
五.解码方法
- 5.1 解题思路
- 5.2 代码：
总结

一、dp问题的通用思路

动态规划问题，按照类别划分其实会分为非常多种，因此一开始的思考方向尤为重要；我个人通常以如下五步作为题目的思考方向：
**1. 确定状态表示:** dp[i]的含义
**2. 确定转移方程**: dp[i]=?
**3. 确定dp表的初始值**
**4. 确定填表顺序**
**5. 确定返回值**

接下来的所有题和文章，均会贯彻这些解题步骤；

二.第N个泰波那契数

在这里插入图片描述

3.1 解题思路：

在这里插入图片描述

3.2 代码:

class Solution {public int tribonacci(int n) {if(n==0) return 0;if(n==1||n==2) return 1;int[] dp=new int[n+1];//初始化dp[0]=0;dp[1]=dp[2]=1;//填表for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}//返回return dp[n];}
}

三. 三步问题

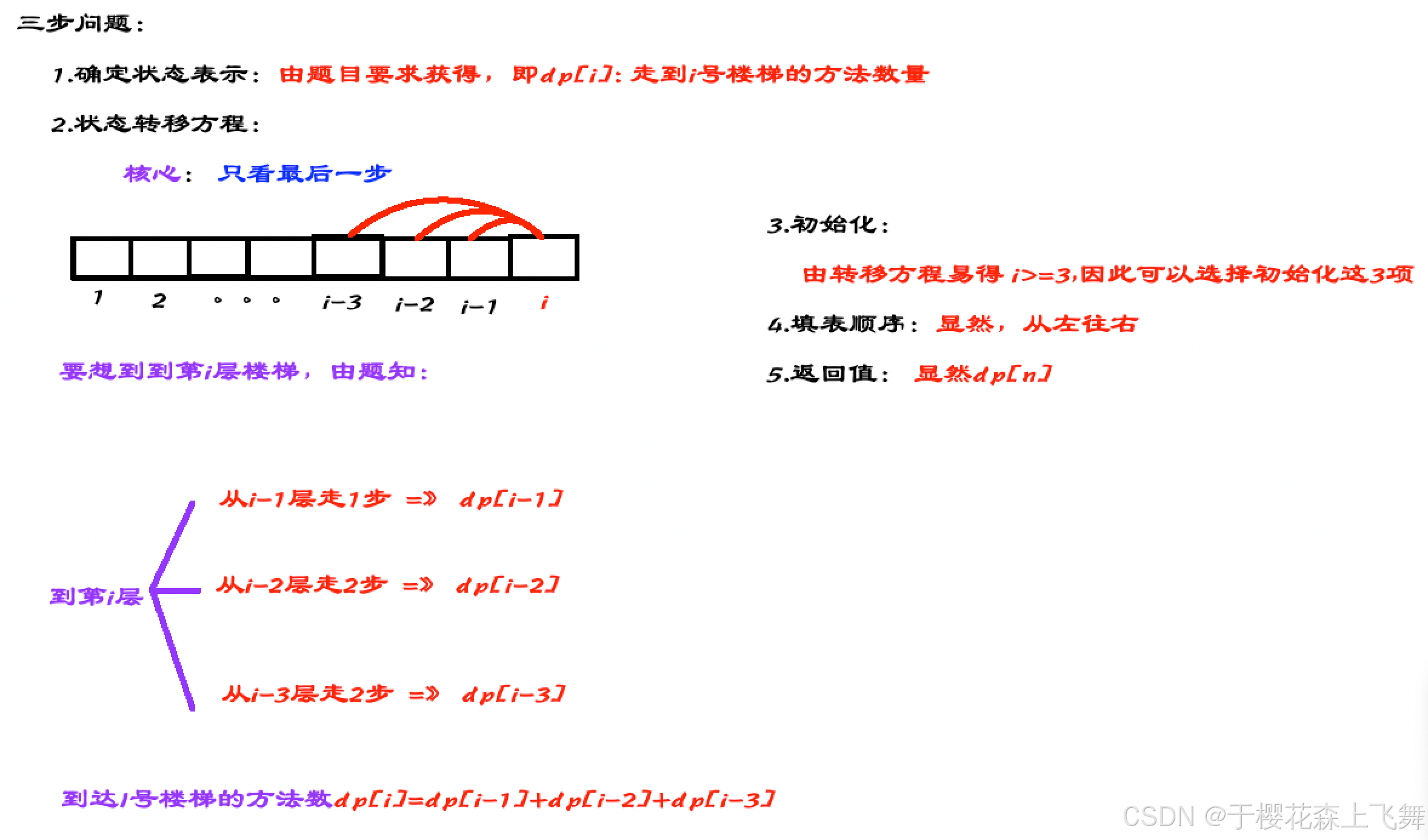
在这里插入图片描述

4.1 解题思路：

在这里插入图片描述

4.2 代码：

class Solution {public int waysToStep(int n) {int ret=1000000007;int[] dp=new int[n+1];if(n==1) return 1;if(n==2) return 2;dp[0]=1;dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++){//同余原理dp[i]=((dp[i-1]+dp[i-2])%ret+dp[i-3])%ret;}return dp[n];}
}

四.使用最小花费爬楼梯

4.1 解题思路：

在这里插入图片描述

4.2 代码：

class Solution {public int minCostClimbingStairs(int[] cost) {int n=cost.length;int[] dp=new int[n+1];//初始化dp[0]=dp[1]=0;//填表for(int i=2;i<=n;i++){//转移方程dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}//返回值return dp[n];}
}

五.解码方法

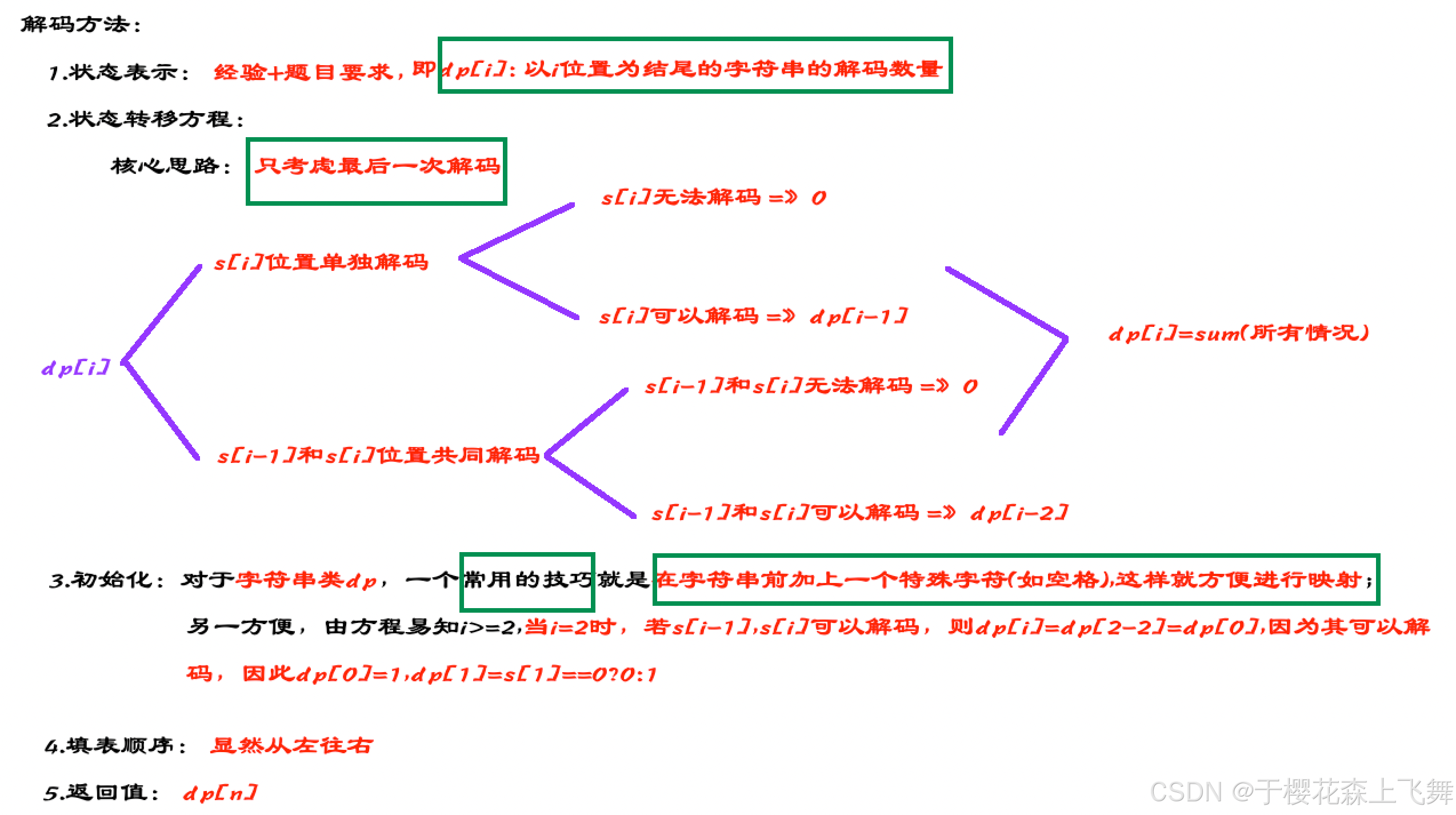
在这里插入图片描述

5.1 解题思路

在这里插入图片描述

5.2 代码：

class Solution {public int numDecodings(String s) {int n=s.length();//特殊处理s=" "+s;int[] dp=new int[n+1];//初始化dp[0]=1;dp[1]=s.charAt(1)=='0'?0:1;for(int i=2;i<=n;i++){//情况1dp[i]+=(s.charAt(i)=='0'?0:dp[i-1]);//情况2if(s.charAt(i-1)!='0'){char a=s.charAt(i-1),b=s.charAt(i);if((a=='1')||(a=='2'&&(b>='0'&&b<='6'))){dp[i]+=dp[i-2];}}}return dp[n];}
}