十字链表和邻接多重表

十字链表和邻接多重表

一、前言

前面讲了有关图的存储结构的概述，今天我将对其中的十字链表和邻接多重表的实现进行一个深入解读~

十字链表和邻接多重表是专门对前面的邻接矩阵和邻接表的优化而设计的存储模式。了解它们的优化机理既是对前面内容的深化，也能锻炼我们思维上的完备性，考虑更加周到。

接下来，就让我们走进这背后的奥妙~

前情回顾

二、十字链表

2.1 本质

正邻接表和逆邻接表的融合。

2.2 剖析

还有什么比图示更清晰呢？

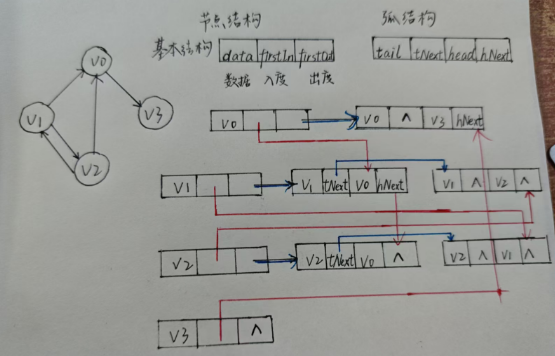
如图，一条边就用一个节点描述（极大地节省了空间，也是其优于邻接矩阵的一个地方）。
顶点结构是存放于数组之中的，是邻接的。（图上不能画得很清楚）

红线都是从顶点的入度（$firstIn$）指针指出去的，你能想到和什么很相似吗？——答案就是逆邻接表
蓝线都是从出度（$firstOut$​）指针指出去的，和正邻接表相似。
这正是淋漓尽致地展现了十字链表是正逆邻接表的融合~

2.3 代码

十字链表的图你是否看明白了呢？它的代码实现起来也是相当复杂，我将尽己所能说的更清楚一些。

2.3.1 定义结构

定义边结构，顶点结构和图结构。

// 十字链表的边结构
typedef struct arcBox
{int tailVertex;				// 弧尾编号，tailVertex作为顶点的出度信息struct arcBox *tailNext;	// 下一个以tailVertex作为弧尾的下一条边int headVertex;				// 弧头编号，以headVertex作为顶点的入度信息struct arcBox *headNext;	// 下一个以headVertex作为弧头的下一条边int weight;					// 弧的权值
} ArcBox;// 十字链表的顶点结构
typedef struct
{int no;const char *show;ArcBox *firstIn;			// 该节点的入度ArcBox *firstOut;			// 该节点的出度
} CrossVertex;// 利用十字链表的结构实现图的结构
typedef struct
{CrossVertex *nodes;int numVertex;int numEdge;				// 定义这些数量，作为释放的评判依据
} CrossGraph;

2.3.2 创建图

easy~

CrossGraph *createCrossGraph(int n)
{CrossGraph *graph = malloc(sizeof(CrossGraph));if(graph == NULL){return NULL;}graph->nodes = malloc(sizeof(CrossVertex) * n);if(graph->nodes == NULL){free(graph);return NULL;}graph->numEdge = 0;graph->numVertex = n;return graph;
}

2.3.3 释放图

void releaseCrossGraph(CrossGraph *graph)
{int numEdges = 0;if (graph){if (graph->nodes)	// 不能直接free nodes{for (int i = 0; i< graph->numVertex; i++){// 从出度开始删，入度也就删掉了。ArcBox *box = graph->nodes[i].firstOut;ArcBox *tmp;while (box){tmp = box;box = box->tailNext;free(tmp);numEdges++;}}printf("release %d edges\n", numEdges);free(graph->nodes);}free(graph);}
}

注意：一条边是由两个指针指向的，只需要利用其中一个指针删掉边即可，不能同时使用，会出现野指针。

2.3.4 初始化

对顶点集的初始化

void initCrossGraph(CrossGraph *graph, const char *names[], int num)
{for(int i = 0; i < num; ++i){graph->nodes[i].no = i;graph->nodes[i].show = names[i];graph->nodes[i].firstIn = graph->nodes[i].firstOut = NULL;}
}

2.3.5 添加边

• 创建边
• 分别从入度和出度两个方面进行头插，建立顶点指向边的联系

// 有向边，从tail指向head
void addCrossARC(CrossGraph *graph, int tail, int head, int w)
{// 创建边ArcBox *box = malloc(sizeof(ArcBox));if(box == NULL){return;}box->weight = w;// 从出度关系上进入插入（头插法）box->tailVertex = tail;box->tailNext = graph->nodes[tail].firstOut;graph->nodes[tail].firstOut = box;// 从入度关系上进入插入（头插法）box->headVertex = head;box->headNext = nodes[head].firstIn;graph->nodes[head].firstIn = box;
}

2.3.6 入度遍历

• 从firstIn开始不断往后遍历

// 计算no编号节点的入度
int inDegreeCrossGraph(CrossGraph *graph, int no)
{int count = 0;ArcBox *box = graph->nodes[no].firstIn;while(box){count++;box = box->headNext;}return count;
}

2.3.7 出度遍历

• 从firstOut开始不断往后遍历

// 计算no编号节点的出度
int outDegreeCrossGraph(CrossGraph *graph, int no)
{int count = 0;ArcBox *box = graph->nodes[no].firstOut;while (box){count++;box = box->tailNext;}return count;
}

2.4 优缺点辨析

2.4.1 优点

• 高效计算入度和出度。
• 快速遍历特定边：方便查找所有指向某顶点或从某顶点指出的边。
• 提高了空间效率：适合稀疏图。

2.4.2 缺点

• 结构复杂：需要维护更多指针。
• 实现复杂：需要维护两个方向的链表。
• 仅适用于有向图，不适合用于无向图。

2.5 应用

• 图论与网络分析：有向图分析，社交网络、任务调度、依赖关系分析。
• 图像处理和计算机图形学：图像压缩、图像分割和稀疏像素操作。

三、邻接多重表

3.1 剖析

如图：

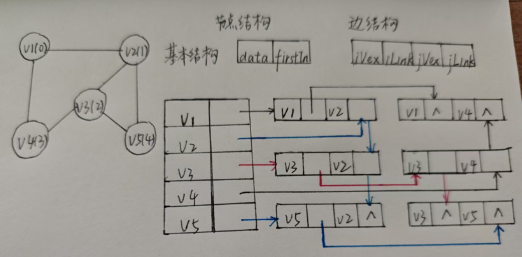
注意：有一条边就存一条边，只需一次malloc（优于邻接矩阵的地方）

重点：$firstIn$在这里无关谁进谁出，表示具有该边的一个端点。同样，这里的$i$和$j$都有可能是边的入口，不再区分入和出，因此遍历时$i$和$j$都要判断。

3.2 代码

3.2.1 定义结构

定义边结构，顶点结构和图结构。

// 定义边结构
typedef struct amlEdge
{int iVex;					// 边的顶点i编号struct amlEdge *iNext;		// 顶点i编号的下一条边int jVex;					// 边的顶点j编号struct amlEdge *jNext;		// 顶点j编号的下一条边int weight;					// 边的权值
} MultiListEdge;// 定义顶点结构
typedef struct
{int no;						// 顶点编号char *show;					// 顶点显示值MultiListEdge *firstEdge;	// 该顶点的边头节点
} MultiListVertex;// 定义表
typedef struct
{MultiListVertex *nodes;		// 顶点空间int vertexNum;				// 约束顶点的数量int edgeNum;				// 图中边的个数
} AdjacencyMultiList;

3.2.2 创建图

easy~

AdjacencyMultiList *createMultiList(int n)
{AdjacencyMultiList *multiList = malloc(sizeof(AdjacencyMultiList));if(multiList == NULL){fprintf(stderr, "malloc failed!\n");return NULL;}multiList->nodes = malloc(sizeof(MultiListVertex) * n);if(multiList->nodes == NULL){fprintf(stderr, "nodes failed!\n");free(multiList);return NULL;}multiList->vertexNum = n;multiList->edgeNum = 0;return multiList;
}

3.2.3 释放图

easy~

void releaseMultiList(AdjacencyMultiList *graph)
{if(graph){if(graph->nodes){free(graph->nodes);}free(graph);}
}

3.2.4 初始化

基本操作，不再赘述~

void initMultiList(AdjacencyMultiList *graph, int n, char *names[])
{for(int i = 0; i < n; ++i){graph->nodes[i].no = i;graph->nodes[i].show = names[i];graph->nodes[i].firstEdge = NULL;}
}

3.2.5 添加边

• 判断端点的合法性
• 创建边
• 建立连接关系：头插法

int insertMultiListEdge(AdjacencyMultiList *graph, int a, int b, int w)
{if(a < 0 || b < 0){return -1;}// 产生这条边MultiListEdge *edge = malloc(sizeof(MultiListEdge));if(edge == NULL){fprintf(stderr, "insert malloc failed!\n");return -1;}edge->weight = w;// 处理a节点的连接关系，使用头插法edge->iVex = 0;edge->iNext = graph->nodes[a].firstEdge;graph->nodes[a].firstEdge = edge;// 处理b节点的连接关系，使用头插法edge->jVex = b;edge->jNext = graph->nodes[b].firstEdge;graph->nodes[b].firstEdge = edge;graph->edgeNum++;return 0;
}

3.2.6 删除边

注意：无向图如果使用邻接表存储，一条边会被处理2次，删除较为复杂。

难点：

• $i$和$j$​等同，不再区分入度和出度
• 两个端点都要找到，才能删除边，防止产生野指针（方法：找到前一个节点来删除）

步骤：

• 从a端点出发找到边的前一个节点
• 从b出发找到边的前一个节点
• 处理关系（a和b都要处理）
• free

int deleteMultiListEdge(AdjacencyMultiList *graph, int a, int b)
{// 找到a编号的前一个边节点MultiListEdge *aPreEdge = NULL;MultiListEdge *aCurEdge = graph->nodes[a].firstEdge;// 循环找a的前一个边节点while(aCurEdge &&!((aCurEdge->iVex == a && aCurEdge->jVex == b) || (aCurEdge->jVex == a && aCurEdge->iVex == b))){aPreEdge = aCurEdge;if(aCurEdge->iVex == a){aCurEdge = aCurEdge->iNext;}else{aCurEdge = aCurEdge->jNext;}}// 不存在a返回空if(aCurEdge == NULL){return -1;}// 找到b编号的前一个边节点——和a是一样的MultiListEdge *bPreEdge = NULL;MultiListEdge *bCurEdge = graph->nodes[b].firstEdge;while(bCurEdge &&!((bCurEdge->iVex == a && bCurEdge->jVex == b) || (bCurEdge->iVex == b && bCurEdge->jVex == a))){bPreEdge = bCurEdge;if(bCurEdge->iVex == b){bCurEdge = bCurEdge->iNext;}else{bCurEdge = bCurEdge->jNext;}}if(bCurEdge == NULL){return -1;}if(aPreEdge == NULL)		// 说明头节点指向的边就是要删除的边，处理a编号的边{if(aCurEdge->iVex == a)	// 当前边从i出发是a{graph->nodes[a].firstEdge = aCurEdge->iNext;// 处理连接关系}else					// 当前边从j出发是a{graph->nodes[a].firstEdge = aCurEdge->jNext;// 处理连接关系}}else{if(aPreEdge->iVex == a && aCurEdge->iVex == a)		// 是通过i出发找到a节点的{aPreEdge->iNext = aCurEdge->iNext;}else if(aPreEdge->iVex == a && aCurEdge->jVex == a)	// 是通过j出发找到a节点的{aPreEdge->iNext = aCurEdge->jNext;}else if(aPreEdge->jVex == a && aCurEdge->iVex == a){aPreEdge->jNext = aCurEdge->iNext;}else{aPreEdge->jNext = aCurEdge->jNext;}}if(bPreEdge == NULL)		// 说明头节点指向的边就是要删除的边，处理b编号的边{if(bCurEdge->iVex == b)	// 当前边从i出发是b{graph->nodes[b].firstEdge = bCurEdge->iNext;}else					// 当前边从j出发是b{graph->nodes[b].firstEdge = bCurEdge->jNext;}}else{if(bPreEdge->iVex == b && aCurEdge->iVex == b)		// 是通过i出发找到b节点的{bPreEdge->iNext = bCurEdge->iNext;}else if(bPreEdge->iVex == b && bCurEdge->jVex == b)	// 是通过j出发找到b节点的{bPreEdge->iNext = bCurEdge->jNext;}else if(bPreEdge->jVex == b && bCurEdge->iVex == b){bPreEdge->jNext = bCurEdge->iNext;}else{bPreEdge->jNext = bCurEdge->jNext;}}free(aCurEdge);// 无论是a还是b释放的都是同一条边graph->edgeNum--;return 0;
}

3.4 优缺点辨析

3.4.1 优点

• 专为无向图设计，处理多重边方便
• 节省空间：一条边仅用一个节点表示

3.4.2 缺点

• 结构复杂：每个边节点要维护多个指针域
• 仅适用于稀疏无向图

3.5 应用

• 社交网络分析：好友关系网络，兴趣群体发现
• 网络分析与建模：电路系统、管道网络和交通规划

四、小结

关于图的存储结构到这里就结束啦~撒花

后期我将深入探讨关于图的相关算法：Kruskal算法，Prim算法等。它们的出现是图走向应用的关键步骤，在生活中的应用甚广~期待$ing$