重邮数字信号处理-实验三z 变换及离散 LTI 系统的 z 域分析
第一题:

代码:
%第一题
B1=[2,16,44,56,32];
A1=[3,3,-15,18,-12];
[B,P,K]=residuez(B1,A1); 实验结果:
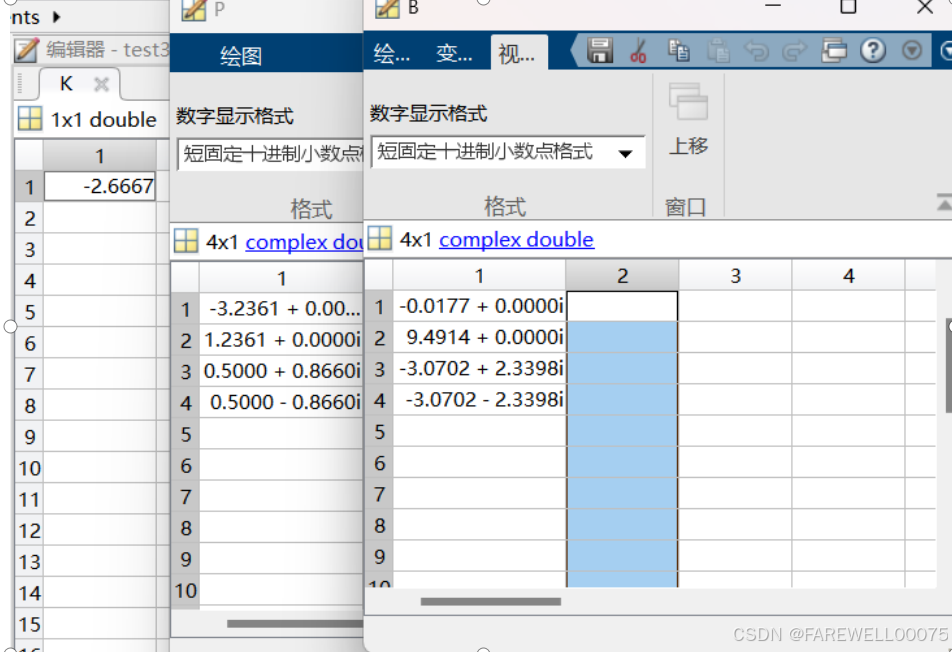
注:这个双击左边的工作区的值就能看见
第二题:

代码:
%第二题第一问
B2=[0,2,-1.6,-0.9];
A2=[1,-2.5,1.96,-0.48];
[B_2_1,P_2_1,K_2_1]=tf2zp(B2,A2);
zplane(B2,A2);
grid on;
legend("零点","极点");
%第二题第二问
B2_2=[0,0,0,1,-1];
A2_2=[1,-0.9,-0.65,0.873,0];
[B_2_2,P_2_2,K_2_2]=tf2zp(B2_2,A2_2);
figure(2);
zplane(B2_2,A2_2);
grid on;
legend("零点","极点"); 实验结果:
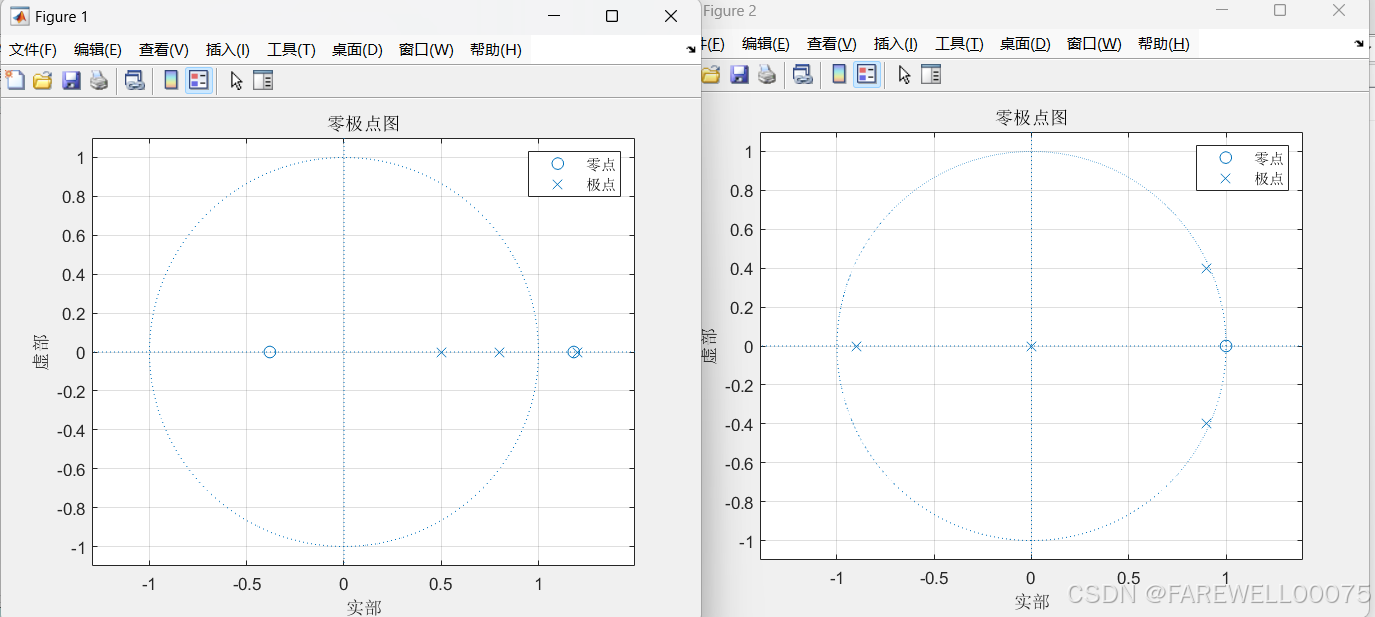
分析:
由稳定性条件条件可知,因果系统要想稳定,必须极点全部位于单位圆内。由实验结果可得,第一小问的零极点图中有一个零点位于单位圆外,故系统不稳定。第二小问的零极点图表示所有极点位于单位圆内,故不稳定。
注:若发现零点和极点错误的重合,也就是出现不应该存在的零点或极点,你只需要补齐到相同的位数,用0补齐即可。
第三题:

代码:
%第三题
B3=[1,0,0];
A3=[1,-3/4,1/8];
[H,w]=freqz(B3,A3,400,"whole");
Hm=abs(H);
Hp=angle(H);
figure(3);
subplot(211);
plot(w,Hm),grid on;
xlabel("\omega(rad/s)"),ylabel("Magnitude");
title("离散系统幅频特性");
subplot(212);
plot(w,Hp),grid on;
xlabel("\omega(rad/s)"),ylabel("Phase");
title("离散系统相频特性"); 实验结果:

第四题:

代码:
%第四题
B4=[1,0,0,0,0,0,0,0,-1];
A4=[1,0,0,0,0,0,0,0,-0.9];
figure(4);
[B4_1,P4,K4]=tf2zp(B4,A4);
subplot(311);
zplane(B4,A4);
grid on;
legend("零点","极点");
[H_2,w_2]=freqz(B4,A4,400,"whole");
Hm_2=abs(H_2);
Hp_2=angle(H_2);
subplot(312);
plot(w_2,Hm_2),grid on;
xlabel("\omega(rad/s)"),ylabel("Magnitude");
title("离散系统幅频特性");
subplot(313);
plot(w_2,Hp_2),grid on;
xlabel("\omega(rad/s)"),ylabel("Phase");
title("离散系统相频特性"); 实验结果:
分析:
(1)由图可得极点位于单位圆内,故该系统稳定。
(3)梳状滤波器
思考题一:
代码:
%思考题一
% 读取音频文件
[audio, fs] = audioread('motherland.wav'); % 加载音频文件
t = (0:length(audio)-1) / fs; % 时间向量,单位为秒
% 提取1到2秒的音频片段
start_sample = fs * 1; % 对应1秒的样本索引
end_sample = fs * 2; % 对应2秒的样本索引
audio_segment = audio(start_sample:end_sample);
% 定义三个滤波器的系数
% H1(z) = z / (z + 0.8)
b1 = [1 0]; % 分子系数
a1 = [1 0.8]; % 分母系数
% H2(z) = z / (z - 1)
b2 = [1 0];
a2 = [1 -1];
% H3(z) = z / (z + 1.2)
b3 = [1 0];
a3 = [1 1.2];
% 对音频片段进行滤波
filtered_audio1 = filter(b1, a1, audio_segment);
filtered_audio2 = filter(b2, a2, audio_segment);
filtered_audio3 = filter(b3, a3, audio_segment);
% 绘制原始和滤波后音频的波形
time_segment = (0:length(audio_segment)-1) / fs; % 1-2秒片段的时间向量
figure(6);
% 原始音频片段的波形
subplot(4,1,1);
plot(time_segment, audio_segment);
title('原始音频片段(1秒到2秒)');
xlabel('时间 (秒)');
ylabel('幅度');
% 滤波后的音频波形
subplot(4,1,2);
plot(time_segment, filtered_audio1);
title('滤波后音频 H_1(z) = z / (z + 0.8)');
xlabel('时间 (秒)');
ylabel('幅度');
subplot(4,1,3);
plot(time_segment, filtered_audio2);
title('滤波后音频 H_2(z) = z / (z - 1)');
xlabel('时间 (秒)');
ylabel('幅度');
subplot(4,1,4);
plot(time_segment, filtered_audio3);
title('滤波后音频 H_3(z) = z / (z + 1.2)');
xlabel('时间 (秒)');
ylabel('幅度'); 实验结果:
分析:
滤波后的信号幅度变化是由于滤波器的频率响应引起的。每个滤波器对应不同的传递函数,其极点和零点的位置不同,对输入信号的频率成分产生不同的放大或衰减效果。因此,经过不同滤波器的信号会呈现出不同的幅度变化。
滤波器一:
在滤波后的波形中,幅度变化不明显,但略微减小了一些。这个滤波器的传递函数形式表明其极点在 -0.8 的位置,靠近单位圆的内部,因此该滤波器表现出轻微的低通特性,对高频分量进行了轻微的衰减,导致音频信号幅度略微降低,但整体变化不显著。
滤波器二:
经过此滤波器后,音频信号的幅度有显著增长,并呈现出一种“漂移”或“增大”的趋势。其传递函数的极点在 1 的位置,位于单位圆上,这导致了系统在边缘稳定或不稳定状态。由于极点在单位圆上,这会导致信号的幅度随时间增加,即滤波器具有“增益放大”的效果。因此,经过此滤波器后,音频信号的幅度会不断增大,这种现象与系统的潜在不稳定性有关。
滤波器三:
此滤波器产生了异常大的输出,几乎达到无限值(或非常大的数字),如图中所示的巨大振幅。这个滤波器的极点在 -1.2,位于单位圆外,这使得系统完全不稳定,导致信号幅度急剧增大,并在某些情况下会发散至无穷大。这种不稳定的行为导致信号的失真,音频信号的幅度也因此被无限放大,失去了原有的波形特性。
思考题二:

代码:
%思考题二
B_think_2=[1,-2,2];
A_think_2=[2,-2,1];
figure(5);
[B_think,P_think,K_think]=tf2zp(B_think_2,A_think_2);
subplot(311);
zplane(B_think_2,A_think_2);
grid on;
legend("零点","极点");
[H_think,w_think]=freqz(B_think_2,A_think_2,400,"whole");
Hm_think=abs(H_think);
Hp_think=angle(H_think);
subplot(312);
plot(w_think,Hm_think),grid on;
xlabel("\omega(rad/s)"),ylabel("Magnitude");
title("离散系统幅频特性");
subplot(313);
plot(w_think,Hp_think),grid on;
xlabel("\omega(rad/s)"),ylabel("Phase");
title("离散系统相频特性"); 实验结果:

分析:
(1)极点全部位于单位圆内,故系统稳定。
(3)从系统的幅频特性图可以看出,幅度在整个频率范围内几乎保持为 1,没有显著的放大或衰减,这表明该系统对不同频率成分没有选择性地增强或衰减,这正是全通滤波器的特征。全通滤波器的核心特点就是保持幅度不变的同时,仅对相位进行调整。相频特性图显示出相位随频率的非线性变化,表明该滤波器对不同频率成分的相位进行不同程度的延迟,而这正是全通滤波器的典型表现。因此,可以判断该系统为全通滤波器。
全通滤波器在实际应用中通常用于相位补偿或延迟调整。例如,在多级滤波器设计中,全通滤波器可以用来补偿其他滤波器引入的相位失真,从而使得系统在特定频率范围内具有较好的相位特性。此外,在音频处理和通信系统中,全通滤波器可用于精确控制信号的相位而不影响其幅度,这对于保持信号波形的完整性非常重要。总体而言,全通滤波器的功能主要集中在相位控制上,而不会改变信号的幅度。



