（七）TRPO 算法 PPO 算法

温故知新

强化学习分类

• Model-based
  • value-based
    动态规划(DP)
• Model-free
  • value-based
    蒙特卡洛(MC)、时序差分(TD)
  • policy-based
    策略梯度算法(如REINFORCE）
  • 集大成者：Actor-Critic 算法/框架 【= Value-based(Critic) + Policy-based(Actor)】

适用于求解问题的类型

• 状态、动作空间均离散且有限
  动态规划、时序差分
• 连续状态，离散动作
  DQN

在线策略 & 离线策略

在线策略（on-policy）算法：学习和采样的策略一样；

如：TD里的 Sarsa、策略梯度的算法 REINFORCE、Actor-Critic 以及两个改进算法——TRPO 和 PPO

离线策略（off-policy）算法：学习和采样的策略不同。

如：TD 里的 Q-learning

老样子，对之前的知识做个简单的分类不要混，其中的 TRPO 和 PPO 是本文的内容，其中 PPO 更是强化学习常用的基准算法。

TRPO 算法

像之前的策略梯度算法和 Actor-Critic 算法存在一个缺陷：当策略网络是深度模型时，沿着策略梯度更新参数，很有可能由于步长太长，策略突然显著变差，进而影响训练效果。TRPO（trust region policy optimization）就是在解决这种问题，使得训练更稳定。
先给个 TRPO 算法的宏观过程：

• 将策略参数化，然后设计相应的目标函数如 $J\left(\theta \right)=E_{s_0}\left[V^{{\pi }_{\theta }}\left(s_0\right)\right]=E_{{\pi }_{\theta }}\left[{\sum }_{t=0}^{\infty }{\gamma }^{t}r\left(s_t,a_t\right)\right]$，同时引入 KL 散度来衡量策略之间的距离，并规定其距离不能太大，也即定了约束条件（孙悟空给他师傅画圈），经过一系列近似、恒等变换操作，我们可将整体问题用下面公式进行刻画：

$$\begin{array}{rl}\underset{\theta }{\max }& {\mathbb{E}}_{\mathbf{s}\sim {\nu }^{{\pi }_{{\theta }_{\text{k}}}}}{\mathbb{E}}_{\mathbf{a}\sim {\pi }_{{\theta }_{\text{k}}}(\cdot |\mathbf{s})}\left[\frac{{\pi }_{\theta }(\mathbf{a}|\mathbf{s})}{{\pi }_{{\theta }_{\text{k}}}(\mathbf{a}|\mathbf{s})}{\mathbf{A}}^{{\pi }_{{\theta }_{\text{k}}}}(\mathbf{s},\mathbf{a})\right]\\ s.t.& {\mathbb{E}}_{\mathbf{s}\sim {\nu }^{{\pi }_{{\theta }_{\text{k}}}}}[D_{\text{KL}}({\pi }_{{\theta }_{\text{k}}}(\cdot |\mathbf{s}),{\pi }_{\theta }(\cdot |\mathbf{s}))]\le \delta \end{array}$$

• 问题描述完就能求解了，TRPO 对上面两个公式用泰勒展开式进行近似，又经过一系列操作，推出更进一步的优化目标，结合 KKT 条件导出其解：${\theta }_{k+1}={\theta }_k+\sqrt{\frac{2\delta }{g^T{H}^{-1}g}}{H}^{-1}g$，为了提高计算效率，令 $\mathbf{x}={\mathbf{H}}^{-1}\mathbf{g}$，这个小问题是二次型优化问题，TRPO 采用共轭梯度法求解
• 为了抵消或者是平滑一下前面近似求解导致的误差，TRPO 采用了线性搜索，你可以理解为试探出合适的步长
• 至于广义优势估计，只是用来估计目标函数中的优势函数 $A$ 的

上面只是草草说明下 TRPO 的做法流程，知道它大概做什么，详细的下面展开：

策略目标

当前策略是 ${\pi }_{\theta }$($\theta$为参数)，对优化目标 $J(\theta )$ 做如下推导：
$$\begin{array}{rl}J(\theta )& ={\mathbb{E}}_{s_0}[V^{{\pi }_{\theta }}(s_0)]\\ & ={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t{V}^{{\pi }_{\theta }}(s_t)-\sum _{t=1}^{\infty }{\gamma }^t{V}^{{\pi }_{\theta }}(s_t)\right]\\ & =-{\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t\left(\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t)\right)\right]\end{array}$$

（一）期望下标从$s_0$ ——> ${\pi }_{{\theta }^{\prime }}$
简单讲，其实换不换下标都是得对$s_0$求期望的，因为$V^{{\pi }_{\theta }}(s_0)$定了${\pi }_{\theta }$后，就只依赖于随机变量$s_0$了，而$s_0$又只服从初始状态分布，这个分布肯定不受策略影响的，所以换下标前后是等价的。展开讲：
${\mathbb{E}}_{s_0}[V^{{\pi }_{\theta }}(s_0)]$：可理解为对于策略${\pi }_{\theta }$，在所有可能的起始状态上的平均性能；
${\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}[V^{{\pi }_{\theta }}(s_0)]$：是策略${\pi }_{{\theta }^{\prime }}$下的整个轨迹分布上求期望。
其中$s_0$是从初始状态分布中采样而来，而不管是什么策略，肯定不影响初始状态分布的，并且我们是对$V^{{\pi }_{\theta }}(s_0)$求期望，这里${\pi }_{\theta }$在迭代结束前是给定死了，那么随机变量就是$s_0$，所以对$V(...)$求期望其实本质就是基于随机变量$s_0$求的，那也就是说，我换了下标后其实计算的本质一样，并不影响，所以二者等价。至于为什么要换？①可以把${\pi }_{\theta }$和${\pi }_{{\theta }^{\prime }}$联系起来；②便于展开成TD误差形式；③可能可以用上重要性采样
（二）等式第三行推导
$$\begin{gathered} \sum _{t=0}^{\infty }{\gamma }^{t}V({\mathbf{s}}_t)-\sum _{t=1}^{\infty }{\gamma }^{t}V({\mathbf{s}}_t)=\sum _{t=0}^{\infty }{\gamma }^{t}V({\mathbf{s}}_t)-\gamma \sum _{t=0}^{\infty }{\gamma }^{t}V({\mathbf{s}}_{t+1}) \\ =\sum _{t=0}^{\infty }{\gamma }^t\left[V({\mathbf{s}}_t)-\gamma V({\mathbf{s}}_{t+1})\right] \\ =-\sum _{t=0}^{\infty }{\gamma }^t\left[\gamma V({\mathbf{s}}_{t+1})-V({\mathbf{s}}_t)\right] \end{gathered}$$

作差，得出新旧策略的目标函数间差距：
$$\begin{array}{rl}J({\theta }^{\prime })-J(\theta )& ={\mathbb{E}}_{s_0}\left[V^{{\pi }_{{\theta }^{\prime }}}(s_0)\right]-{\mathbb{E}}_{s_0}\left[V^{{\pi }_{\theta }}(s_0)\right]\\ & ={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)\right]+{\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t\left(\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t)\right)\right]\\ & ={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t\left[r(s_t,a_t)+\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t)\right]\right]\end{array}$$

将时序差分残差定义为优势函数 $A$：
$$\begin{array}{rl}& ={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t{A}^{{\pi }_{\theta }}({\mathbf{s}}_t,{\mathbf{a}}_t)\right]\\ & =\sum _{t=0}^{\infty }{\gamma }^t{\mathbb{E}}_{s_t\sim P_t^{{\pi }_{{\theta }^{\prime }}}}{\mathbb{E}}_{a_t\sim {\pi }_{{\theta }^{\prime }}(\cdot |{\mathbf{s}}_t)}\left[A^{{\pi }_{\theta }}({\mathbf{s}}_t,{\mathbf{a}}_t)\right]\\ & =\frac{1}{1-\gamma }{\mathbb{E}}_{\mathbf{s}\sim {\nu }^{{\pi }_{{\theta }^{\prime }}}}{\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |\mathbf{s})}\left[A^{{\pi }_{\theta }}(\mathbf{s},\mathbf{a})\right]\end{array}$$

关于第三行的推导：

• 先定义下折扣状态访问分布：${\nu }^{{\pi }_{{\theta }^{\prime }}}\left(s\right)=\left(1-\gamma \right){\sum }_{t=0}^{\infty }{\gamma }^t{P}_t^{{\pi }_{{\theta }^{\prime }}}\left(s\right)$，关于为什么前面加了折扣因子，其实主要是为了归一化，如下：
  $$\sum _s\sum _{t=0}^{\infty }{\gamma }^t{P}_t^{{\pi }_{/\mathcal{E}}}(s)=\sum _{t=0}^{\infty }\sum _s{\gamma }^t{P}_t^{{\pi }_{/\mathcal{E}}}(s)=\sum _{t=0}^{\infty }{\gamma }^t\cdot \left(\sum _s{P}_t^{{\pi }_{/\mathcal{E}}}(s)\right)=\sum _{t=0}^{\infty }{\gamma }^t\cdot 1=\frac{1}{1-\gamma }$$
  乘$(1-\gamma )$后就有${\sum }_{\mathbf{s}}{\mathbf{\nu }}^{{\mathbf{\pi }}_{{\mathbf{\theta }}^{\prime }}}(\mathbf{s})=1$；
• 其次对第三行推导补充如下：
  $$\begin{array}{rl}\sum _{t=0}^{\infty }{\gamma }^t{\mathbb{E}}_{s_l\sim P_t^{{\pi }_{{\theta }^{\prime }}}}{\mathbb{E}}_{a_l\sim {\pi }_{{\theta }^{\prime }}(\cdot |s_l)}\left[A^{{\pi }_{\theta }}(s_t,a_t)\right]& =\sum _{t=0}^{\infty }{\gamma }^t\sum _s{P}_t^{{\pi }_{{\theta }^{\prime }}}(s){\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |s)}\left[A^{{\pi }_{\theta }}(s,a)\right]\\ & =\sum _s\left[\sum _{t=0}^{\infty }{\gamma }^t{P}_t^{{\pi }_{{\theta }^{\prime }}}(s)\right]{\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |s)}\left[A^{{\pi }_{\theta }}(s,a)\right]\\ & =\sum _s\frac{{\nu }^{{\pi }_{{\theta }^{\prime }}}(s)}{1-\gamma }{\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |s)}\left[A^{{\pi }_{\theta }}(s,a)\right]\\ & =\frac{1}{1-\gamma }\sum _s{\nu }^{{\pi }_{{\theta }^{\prime }}}(s){\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |s)}\left[A^{{\pi }_{\theta }}(s,a)\right]\\ & =\frac{1}{1-\gamma }{\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }^{\prime }}}}{\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |s)}\left[A^{{\pi }_{\theta }}(s,a)\right]\end{array}$$

好了，我们把目标函数简化成上式，在该式中，如果我们能保证等式右边非负，就能保证策略性能提升。但问题是直接求它很困难，因为 ${\pi }_{{\theta }^{\prime }}$ 是我们要求解的策略，但我们又要用它来收集样本，如果采取把所有可能的新策略都拿来收集数据，然后判断哪个策略满足上述条件的做法显然是不现实的。
所以 TRPO 采用如下替代优化目标：
$$L_{\theta }({\pi }_{{\theta }^{\prime }})=J(\theta )+\frac{1}{1-\gamma }{\mathbb{E}}_{s\sim {\nu }^{{\pi }_{\theta }}}{\mathbb{E}}_{a\sim {\pi }_{\theta }(\cdot |s)}\left[\frac{{\pi }_{{\theta }^{\prime }}(a|s)}{{\pi }_{\theta }(a|s)}{A}^{{\pi }_{\theta }}(s,a)\right]$$

解释：

1. 状态分布近似（${\pi }_{{\theta }^{\prime }}\approx {\pi }_{\theta }$）
   前提是当新旧策略非常接近时，状态访问分布变化很小，故能做如下近似：$J({\theta }^{\prime })-J(\theta )\approx \frac{1}{1-\gamma }{\mathbb{E}}_{s\sim {\nu }^{{\pi }_{\theta }}}{\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |s)}[A^{{\pi }_{\theta }}(s,a)]$

2. 重要性采样
   重要性采样允许我们用一个容易采样的分布 $q$ 来估计关于另一个分布 $p$ 的期望，通过给每个样本加权重 $\frac{p}{q}$ 来修正分布差异。值得说明的是，重要性采样是无偏估计，但若 $q$、$p$ 分布相差太大，则权重 $\frac{p}{q}$ 不稳定，会导致方差大，所以上一步我们假设了新旧策略接近。故有如下式子：${\mathbb{E}}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot |s)}[A^{{\pi }_{\theta }}(s,a)]={\mathbb{E}}_{a\sim {\pi }_{\theta }(\cdot |s)}\left[\frac{{\pi }_{{\theta }^{\prime }}(a|s)}{{\pi }_{\theta }(a|s)}{A}^{{\pi }_{\theta }}(s,a)\right]$

结合上述两步，最终就是上面替代后的优化目标了。

好了，聪明的你经过操作，问题变得可求解，但还有一个问题：前面我们说近似的前提是新旧策略非常接近，那怎么去衡量呢？
TRPO 使用了 KL散度来衡量策略之间的距离（这里，对于KL散度你只需要知道能量化两个策略的差异就行），则整个问题可以变成一个带约束的优化函数了，我们描述如下：
$$\begin{array}{rl}& \underset{{\theta }^{\prime }}{\max }{L}_{\theta }({\theta }^{\prime })\\ & s.t.{\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }_k}}}[D_{KL}({\pi }_{{\theta }_k}(\cdot |s),{\pi }_{{\theta }^{\prime }}(\cdot |s))]\le \delta \end{array}$$

补充：
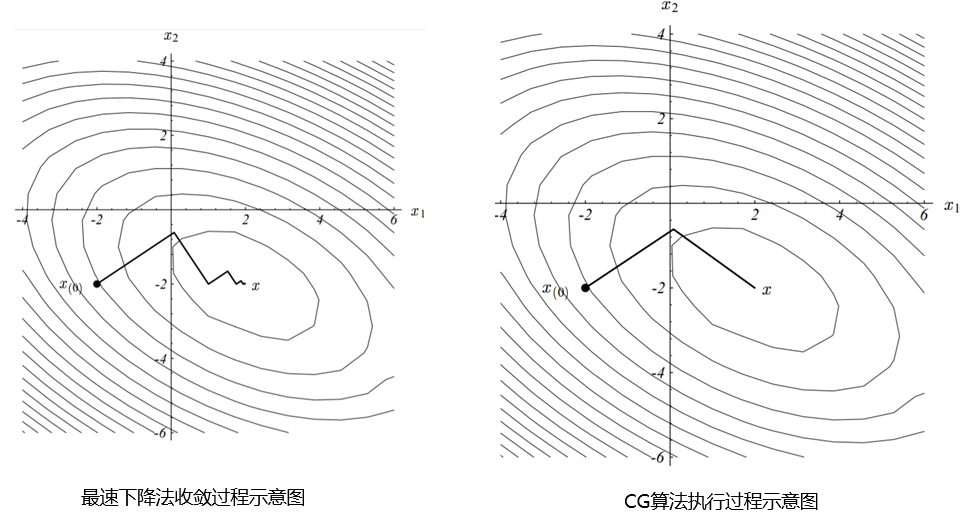
从上式易知，约束条件定义了策略空间中的一个 KL 球，被称为信任区域。（打个不太恰当的比喻：孙悟空给他师傅画的圈圈）在这个区域中，我们认为新旧策略的分布足够接近，可以认为当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致，进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。

如上诠释了 TRPO 的原理，左图是当完全不设置信任区域，策略的梯度更新可能导致策略的性能骤降；右图设置了信任区域，可以保证每次策略的梯度更新时性能都有所提升。

近似求解

这里的近似求解也是类似的出发点，直接求解上式带约束的优化问题困难，所以 TRPO 分别对目标函数和约束条件在 ${\theta }_k$ （也即之前的 $\theta$，代表旧策略的参数）处采取泰勒展开进行近似，如下：
$${\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }_k}}}{\mathbb{E}}_{a\sim {\pi }_{{\theta }_k}(\cdot |s)}\left[\frac{{\pi }_{{\theta }^{\prime }}(a|s)}{{\pi }_{{\theta }_k}(a|s)}{A}^{{\pi }_{{\theta }_k}}(s,a)\right]\approx g^T({\theta }^{\prime }-{\theta }_k)$$
$${\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }_k}}}[D_{KL}({\pi }_{{\theta }_k}(\cdot |s),{\pi }_{{\theta }^{\prime }}(\cdot |s))]\approx \frac{1}{2}({\theta }^{\prime }-{\theta }_k{)}^{T}H({\theta }^{\prime }-{\theta }_k)$$

目标函数的泰勒展开：

• 我令 $F={\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }_k}}}{\mathbb{E}}_{a\sim {\pi }_{{\theta }_k}(\cdot |s)}[...]$，则其泰勒展开大致如下：$F({\theta }^{\prime })\approx F({\theta }_k)+{\nabla }_{{\theta }^{\prime }}F({\theta }_k{)}^{\top }({\theta }^{\prime }-{\theta }_k)$
• 其中，当${\theta }^{\prime }={\theta }_k$，重要性采样比值为1，此时有 $F({\theta }_k)={\mathbb{E}}_{s,a\sim {\pi }_k}\left[A^{{\pi }_k}(s,a)\right]$，而对于任意策略，其优势函数关于动作的期望为0，即 ${\mathbb{E}}_{a\sim {\pi }_k}\left[A^{{\pi }_k}(s,a)\right]=0$，综上可得：$F({\theta }_k)={\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }_k}}}[0]=0$
• 令 $g={\nabla }_{{\theta }^{\prime }}F({\theta }_k)={\nabla }_{{\theta }^{\prime }}{\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }_k}}}{\mathbb{E}}_{a\sim {\pi }_{{\theta }_k}(\cdot |s)}\left[\frac{{\pi }_{{\theta }^{\prime }}(a|s)}{{\pi }_{{\theta }_k}(a|s)}{A}^{{\pi }_{{\theta }_k}}(s,a)\right]$

约束条件的泰勒展开：

• KL 散度的定义如下：$D_{KL}({\pi }_{{\theta }_k}(\cdot |s),{\pi }_{{\theta }^{\prime }}(\cdot |s))={\mathbb{E}}_{a\sim {\pi }_{{\theta }_k}(\cdot |s)}\left[\log \frac{{\pi }_{{\theta }_k}(a|s)}{{\pi }_{{\theta }^{\prime }}(a|s)}\right]$，
  通常考虑平均 KL 散度：${\mathbb{E}}_{s\sim {\nu }^{{\pi }_{{\theta }_k}}}[D_{KL}({\pi }_{{\theta }_k},{\pi }_{{\theta }^{\prime }})]$。
• 为方便说明，我们令 $d({\theta }^{\prime })=D_{KL}({\pi }_{{\theta }_k},{\pi }_{{\theta }^{\prime }})$。
  则有：$d({\theta }^{\prime })\approx d({\theta }_k)+{\nabla }_{{\theta }^{\prime }}d({\theta }_k{)}^{\top }({\theta }^{\prime }-{\theta }_k)+\frac{1}{2}({\theta }^{\prime }-{\theta }_k{)}^{\top }{\nabla }_{{\theta }^{\prime }}^{2}d({\theta }_k)({\theta }^{\prime }-{\theta }_k)$。
  可能你会有疑惑，约束条件不是期望的形式吗，不应该是对整个期望展开吗，为什么这里直接先对期望内部的 $D_{KL}$ 展开了？因为期望是线性算子，使得我们可以先对内部进行近似展开，再求期望。
• 其中，当${\theta }^{\prime }={\theta }_k$，新旧策略相同，则两个分布相同，故有 $d({\theta }_k)=0$；
• 计算一阶导：
  变换一下 $d({\theta }^{\prime })={\sum }_a{\pi }_{{\theta }_k}(a|s)\left[\log {\pi }_{{\theta }_k}(a|s)-\log {\pi }_{{\theta }^{\prime }}(a|s;{\theta }^{\prime })\right]$，
  上式对 ${\theta }^{\prime }$ 求导并代入 ${\theta }_k$： ${\nabla }_{\theta }^{\prime }d({\theta }_k)=-{\sum }_a{\pi }_{{\theta }_k}(a|s){\nabla }_{{\theta }^{\prime }}\log \pi (a|s;{\theta }_k)$，则有 :
  $$\begin{array}{rl}\sum _a{\pi }_{{\theta }_k}(a|s){\nabla }_{{\theta }^{\prime }}\log \pi (a|s;{\theta }_k)& =\sum _a{\pi }_{{\theta }_k}(a|s)\frac{{\nabla }_{{\theta }^{\prime }}\pi (a|s;{\theta }_k)}{\pi (a|s;{\theta }_k)}\\ & =\sum _a{\pi }_{{\theta }_k}(a|s)\frac{{\nabla }_{{\theta }^{\prime }}\pi (a|s;{\theta }_k)}{{\pi }_{{\theta }_k}(a|s)}\\ & =\sum _a{\nabla }_{{\theta }^{\prime }}\pi (a|s;{\theta }_k)\end{array}$$
  而 ${\sum }_a\pi (a|s;\theta )=1$，对 $\theta$ 求导就得 ${\sum }_a{\nabla }_{\theta }\pi (a|s;\theta )=0$，故上式的一阶导 ${\nabla }_{\theta }^{\prime }d({\theta }_k)=0$。
• 计算二阶导：
  这里用黑塞矩阵（Hessian matrix）H 代表二阶梯度，也即 $H={\nabla }_{\theta }^2{\bar{D}}_{\mathrm{KL}}({\theta }_{\mathrm{old}},\theta ){|}_{\theta ={\theta }_{\mathrm{old}}}$
  综上就是所示的约束条件的泰勒展开形式。

自此，我们讲问题的优化目标又转化为：
$$\begin{array}{rl}& {\theta }_{k+1}=\arg \underset{{\theta }^{\prime }}{\max }{g}^T({\theta }^{\prime }-{\theta }_k)\\ & s.t.\frac{1}{2}({\theta }^{\prime }-{\theta }_k{)}^{T}H({\theta }^{\prime }-{\theta }_k)\le \delta \end{array}$$
根据KKT条件直接导出上述问题的解：
$${\theta }_{k+1}={\theta }_k+\sqrt{\frac{2\delta }{g^T{H}^{-1}g}}{H}^{-1}g$$

共轭梯度

共轭梯度法（Conjugate Gradients）是稀疏线性方程组迭代求解法里面最优秀的方法，是解决大型线性方程组问题最流行的迭代算法，如：$\mathbf{A}\vec{x}=\vec{b}$。
回到我们的问题，前面我们推导出问题的解，但存在不足：计算和存储黑塞矩阵的逆非常耗时耗内存，所以 TRPO 采取直接计算 $x=H^{-1}g$（$x$ 为参数更新方向）。
假设满足 KL 距离约束的参数更新时的最大步长为 $\beta$，则根据 KL 距离约束条件，有$\frac{1}{2}(\beta x{)}^{T}H(\beta x)=\delta$，解得 $\beta =\sqrt{\frac{2\delta }{x^{T}Hx}}$，此时参数更新方式为：
$${\theta }_{k+1}={\theta }_k+\sqrt{\frac{2\delta }{x^{T}Hx}}x$$
那么，现在问题就是求这个 $x$，根据上文 TRPO 的设想，问题转化为解线性方程组：$Hx=g$，实际 H 是对称正定矩阵，这么一转化就很适合用共轭梯度法求：

对于二次型优化问题，我们熟悉的梯度下降法是通过沿着当前点 $x_0$ 的梯度方向寻找一个新点 $x_1$，在点 $x_1$ 处的梯度跟点 $x_0$ 处的梯度刚好正交，从而确定当前点 $x_0$ 的前进步长的；而共轭梯度法是构建一组线性无关向量（空间维度决定这组向量有多少个，如2维就2个无关向量）作为搜索方向（前进方向），显见，这组无关向量肯定能表示出当前点 $x_0$ 与目标值点 $x$ 间的误差向量（也即误差向量是这些无关向量的线性组合，每个搜索向量都是误差向量的分量），而 CG 就是通过每次迭代时消除搜索向量（也即消除误差向量的分量）达到目标，从而最优化问题。
上述伪代码流程中，for 循环里前三个迭代式就是类似梯度下降法的思想，而不同于梯度下降的是其利用的是搜索向量 $p_k$ 而不完全是梯度，后两个迭代式就是在对搜索向量 $p_k$ 进行迭代更新的。

其实，粗糙得说，CG 跟梯度下降都是在求梯度，只是二者对步长的确定不同，因为二者的迭代路径其实通过平移后一致：

线性搜索

其实就是对抗之前近似操作的误差，让更新的步长更可靠

问题不足：前面对求解问题用到泰勒展开近似，而非精确解，因此，按理论的 $\sqrt{\frac{2\delta }{x^{T}Hx}}$ 步长去更新参数，可能导致 ${\theta }^{\prime }$ 未必优于 $\theta$，或未必满足 KL散度约束。
改进：TRPO 在每次迭代的最后进行一次线性搜索（Line Search），以确保找到满足条件。
具体讲，更新方式修改为 ${\theta }_{k+1}={\theta }_k+{\alpha }^i\sqrt{\frac{2\delta }{x^{T}Hx}}x$，我们目标是找到一个最小的非负正数 $i$，使得 ${\theta }_{k+1}$ 既能满足 KL散度约束，又能提升目标函数，即 $L_{\theta }({\theta }^{\prime })\ge L_{\theta }({\theta }_k)$。

体现在代码就是计算出来然后作比较：

if new_obj > old_obj and kl_div < self.kl_constraint:return new_para

广义优势估计

填一下优势函数 $A$ 的坑的…
之前推导那么多，还有一个漏了，就是优势函数，求梯度 $g$ 需要到的。那就是如何去估计 $A$ 的问题，目前常用的一种方法为广义优势估计（Generalized Advantage Estimation，GAE）。

用 ${\delta }_t=r_t+\gamma V(s_{t+1})-V(s_t)$ 表示时序差分误差，根据多步时序差分的思想，有：
$$\begin{array}{rlrl}& A_t^{(1)}={\delta }_t& & =-V(s_t)+r_t+\gamma V(s_{t+1})\\ & A_t^{(2)}={\delta }_t+\gamma {\delta }_{t+1}& & =-V(s_t)+r_t+\gamma r_{t+1}+{\gamma }^{2}V(s_{t+2})\\ & A_t^{(3)}={\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2}& & =-V(s_t)+r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+{\gamma }^{3}V(s_{t+3})\\ & :& & \\ & A_t^{(k)}=\sum _{l=0}^{k-1}{\gamma }^l{\delta }_{t+l}& & =-V(s_t)+r_t+\gamma r_{t+1}+\dots +{\gamma }^{k-1}{r}_{t+k-1}+{\gamma }^{k}V(s_{t+k})\end{array}$$

$k$：理解为步数

GAE 将这些不同步数的优势估计进行指数加权平均：
$$\begin{array}{rl}{A}_t^{GAE}& =(1-\lambda )(A_t^{(1)}+\lambda A_t^{(2)}+{\lambda }^2{A}_t^{(3)}+\cdots )\\ & =(1-\lambda )({\delta }_t+\lambda ({\delta }_t+\gamma {\delta }_{t+1})+{\lambda }^2({\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2})+\cdots )\\ & =(1-\lambda )(\delta (1+\lambda +{\lambda }^2+\cdots )+\gamma {\delta }_{t+1}(\lambda +{\lambda }^2+{\lambda }^3+\cdots )+{\gamma }^2\\ & =(1-\lambda )\left({\delta }_t\frac{1}{1-\lambda }+\gamma {\delta }_{t+1}\frac{\lambda }{1-\lambda }+{\gamma }^2{\delta }_{t+2}\frac{{\lambda }^2}{1-\lambda }+\cdots \right)\\ & =\sum _{l=0}^{\infty }(\gamma \lambda {)}^l{\delta }_{t+l}\end{array}$$

其中，$\lambda \in [0,1]$ 即权重，因为 $1+\lambda +{\lambda }^2+{\lambda }^3+\cdots =\frac{1}{1-\lambda }$，所以整体需要除以总权重之和，也即乘 $(1-\lambda )$。

• 代入 0 时：
  $A_t^{(GAE)}={\sum }_{i=0}^{\infty }(0{)}^i{\delta }_{t+i}=(1)\ast {\delta }_{t+0}+0+0+...={\delta }_t=r_t+\gamma V(s_{t+1})-V(s_t)$
  此时，优势函数的估计完全依赖于当前的单步奖励 $r_t$ 和下一个状态的价值估计 $V(s_{t+1})$。其估计严重依赖 $V$ 的准确性，但只涉及一次奖励采样和一个价值函数估计，引入的随机性较少，总结就是高偏差，低方差。
• 代入 1 时：
  $A_t^{(GAE)}={\sum }_{i=0}^{\infty }{\gamma }^i{\delta }_{t+i}=-V(s_t)+{\sum }_{i=0}^{\infty }{\gamma }^i{r}_{t+i}$（中间推导利用上文 $A_t^{(k)}={\sum }_{l=0}^{k-1}{\gamma }^l{\delta }_{t+l}$）
  此时，优势函数的估计依赖于从当前时刻到回合结束的所有实际奖励。其估计基于大量真实的奖励信号，而不是仅仅依赖价值函数的预测，因此它更接近真实的优势值，但由于累计了未来很多步的随机奖励，而这些奖励本身是采样的、有随机性的，所以最终估计值的方差会很高，总结就是低偏差，高方差。

GAE 的巧妙之处就在于，通过设置 $\lambda \in [0,1]$（例如 0.95），我们可以在两种极端之间找到一个理想的折中点，既获得了蒙特卡洛方法低偏差、更准确的优势，又利用了时序差分方法低方差、更稳定的优点。

TRPO 算法流程(伪代码)

最后，给出 TRPO 的全部过程：

可见，TRPO 算法属于在线策略学习方法，每次策略训练仅使用上一轮策略采样的数据，是基于策略的深度强化学习算法中十分有代表性的工作之一。

PPO 算法

TRPO 很强，但计算好复杂，简单点才是美，PPO（Proximal Policy Optimization，近端策略优化) 就是简化了 TRPO 的计算，同样的，TRPO 的优化目标：
$$\begin{array}{rl}\underset{\theta }{\max }& {\mathbb{E}}_{\mathbf{s}\sim {\nu }^{{\pi }_{{\theta }_{\text{k}}}}}{\mathbb{E}}_{\mathbf{a}\sim {\pi }_{{\theta }_{\text{k}}}(\cdot |\mathbf{s})}\left[\frac{{\pi }_{\theta }(\mathbf{a}|\mathbf{s})}{{\pi }_{{\theta }_{\text{k}}}(\mathbf{a}|\mathbf{s})}{\mathbf{A}}^{{\pi }_{{\theta }_{\text{k}}}}(\mathbf{s},\mathbf{a})\right]\\ s.t.& {\mathbb{E}}_{\mathbf{s}\sim {\nu }^{{\pi }_{{\theta }_{\text{k}}}}}[D_{\text{KL}}({\pi }_{{\theta }_{\text{k}}}(\cdot |\mathbf{s}),{\pi }_{\theta }(\cdot |\mathbf{s}))]\le \delta \end{array}$$
PPO 使用更为简单的解法，具体而言，PPO 有两种形式：① PPO-惩罚，② PPO-截断

PPO-惩罚（PPO-Penalty）

PPO-Penalty 使用拉格朗日乘数法直接将 KL 散度的限制放到目标函数中，使得成为一个无约束的优化问题，然后迭代更新 $\beta$，所以惩罚其实就是指减去了 $\beta D_{KL}$，优化目标转化为：
$$\arg \underset{\theta }{\max }{\mathbb{E}}_{s\sim \nu }{\ast }_{{\theta }_k}{\mathbb{E}}_{a\sim {\pi }_{{\theta }_k}(\cdot |s)}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_k}(a|s)}{A}^{{\pi }_{{\theta }_k}}(s,a)-\beta D_{KL}[{\pi }_{{\theta }_k}(\cdot |s),{\pi }_{\theta }(\cdot |s)]\right]$$
令 $d_k=D_{KL}^{{\nu }^{{\pi }_{{\theta }_k}}}({\pi }_{{\theta }_k},{\pi }_{\theta })$（旧策略访问状态分布下，新旧策略的 KL 散度），预设超参数 $\delta$（用于限制学习策略和之前一轮策略的差距），规定参数 $\beta$ 更新规则：

1. 如果 $d_k<\delta /1.5$，那么 ${\beta }_{k+1}={\beta }_k/2$
2. 如果 $d_k>\delta \times 1.5$，那么 ${\beta }_{k+1}={\beta }_k\times 2$
3. 否则 ${\beta }_{k+1}={\beta }_k$

可知，PPO-Penalty 采用自适应调整 $\beta$ 的方法，使得 KL 散度 $d_k$ 维持在某个目标值 $\delta$ 附近。

设想如果固定 $\beta$ 为某个值会有什么问题？

• 若 $\beta$ 过大，惩罚就过强，策略更新会十分保守，学习训练缓慢
• 若 $\beta$ 过小，惩罚就太弱，策略更新幅度可能过大，训练不稳定

分析一下更新条件：

• 如果 $d_k<\delta /1.5$，说明 KL 散度偏小，策略差距小，可以允许更大的更新幅度，所以可以减弱惩罚，即 ${\beta }_{k+1}={\beta }_k/2$；
• 如果 $d_k>\delta \times 1.5$，说明 KL 散度偏大，策略差距大，需要限制较小的更新幅度以防止不稳定，所以应该加强惩罚，即 ${\beta }_{k+1}={\beta }_k\times 2$；
• 否则 $\delta /1.5\le d_k\le \delta \times 1.5$，KL 散度在可接受范围内，$\beta$ 不变。

可见，PPO-Penalty 的设计原理是同样是限制新旧策略的差距在合理的范围内，体现在让 $d_k$ 靠近 $\delta$，利用比例控制思想，本质还是反馈控制：

• KL 太小 → 惩罚减弱 → $L_{\theta }({\theta }^{\prime })$ 下次的更新步长可能变大 → KL 增加；
• KL 太大 → 惩罚增强 → $L_{\theta }({\theta }^{\prime })$ 下次的更新步长可能变小 → KL 减小。

PPO-截断（PPO-Clip）

PPO-Clip 是 PPO 更常用的形式，它直接用裁剪比率来限制更新幅度：
$$\arg \max {\mathbb{E}}_{s\sim \nu }{\mathbb{E}}_{a\sim {\pi }_{s_k}(\cdot |s)}\left[\min \left(\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_k}(a|s)}{A}^{{\pi }_{{\theta }_k}}(s,a),\mathrm{clip}\left(\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_k}(a|s)},1-ϵ,1+ϵ\right)A^{{\pi }_{{\theta }_k}}(s,a)\right)\right]$$
其中，$\mathrm{clip}(x,l,r):=\max (\min (x,r),l)$，即把 $x$ 限制在 $[l,r]$ 内，而 $ϵ$ 是一个超参数，由式子可知：

• 当 $A^{{\pi }_{{\theta }_k}}(s,a)>0$，代表好动作，鼓励更新，但别太过头，最多更新 $1+ϵ$ 即可；
• 当 $A^{{\pi }_{{\theta }_k}}(s,a)<0$，代表坏动作，抑制更新，但也别一棍子打死，最低抑制到 $1-ϵ$ 即可。
  
  上图是 PPO-Clip 的示意图，很形象的说明了截断操作。
  可见，PPO-Clip 的设计原理是同样也是限制新旧策略的差距在合理的范围内，而它体现在使用超参数 $ϵ$ 配合截断比率，实现更简单，效果更稳定，相比之前的复杂计算、麻烦的迭代，PPO-Clip 更加巧妙和简洁高效！

小结

小结一下：

	PPO-Penalty	PPO-Clip
约束方式	在目标函数中添加自适应KL惩罚项	在目标函数中直接采用截断比率
超参数	初始惩罚系数 $\beta$，KL限制 $\delta$	截断范围 $ϵ$
调节机制	根据KL散度动态调整 $\beta$	固定的 $ϵ$，通过目标函数设计内在约束
优点	理论上能更精确地控制KL散度	实现更简单，效果更稳定，是更常用的版本

最后，值得说明的是，TRPO 和 PPO 都属于在线策略学习算法，即使优化目标中包含重要性采样的过程，但其实只用到了上一轮策略的数据，而非过去所有策略的数据。

---

参考资料

1. https://hrl.boyuai.com/
2. https://github.com/wangshusen/DRL/blob/master/Slides/1_Basics_3.pdf
3. https://blog.csdn.net/qaqwqaqwq/article/details/123421989