回溯专题：子集/全排列问题

目录

题目链接

子集问题思路分析

代码

全排列问题思路分析

总结

---

题目链接

78. 子集 - 力扣（LeetCode）

46. 全排列 - 力扣（LeetCode）

这两道题都是来源于力扣hot 解题思路其实大同小异

子集问题思路分析

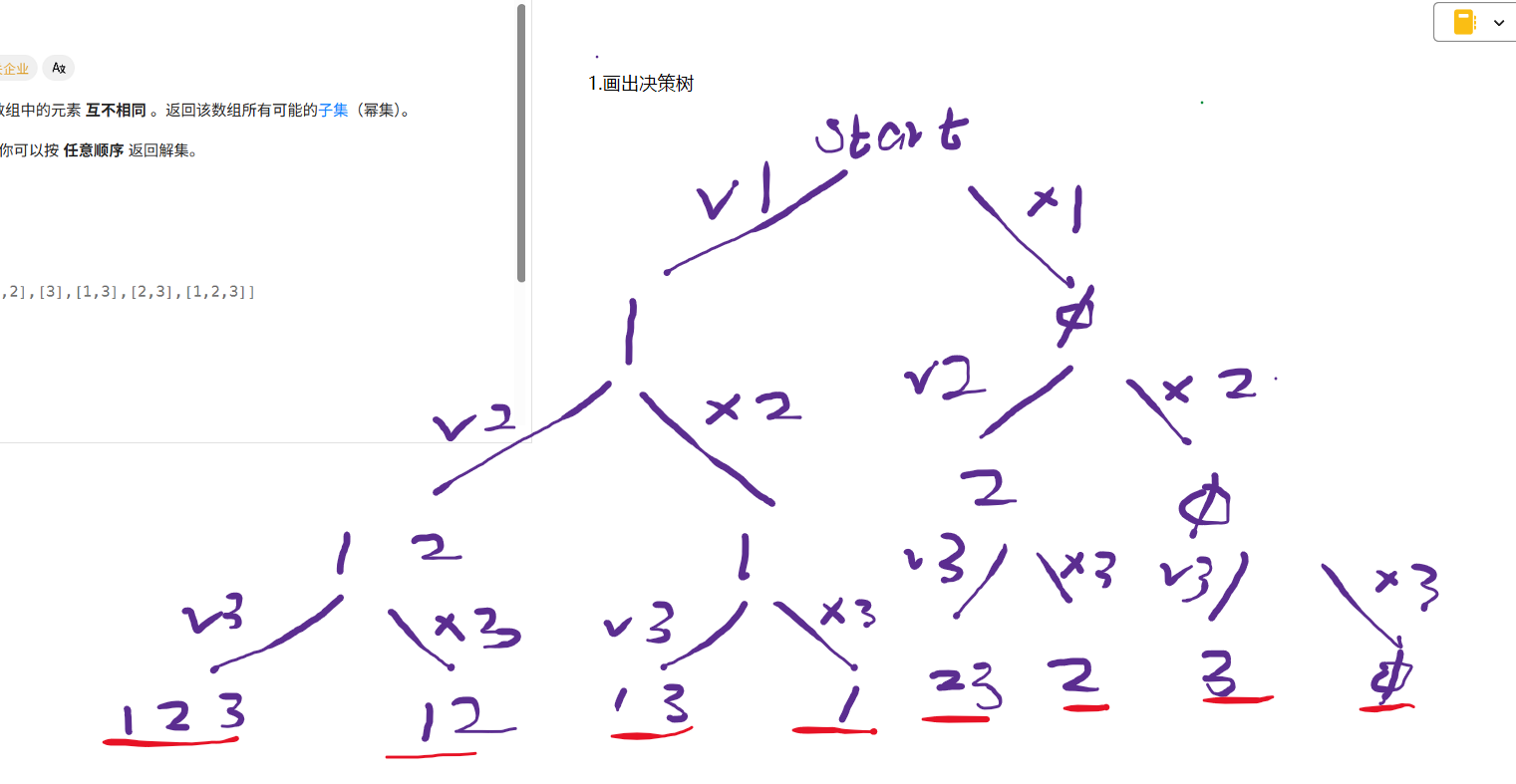
重点关注：1.引入全局变量path，ret的好处（大大简化函数头的设计）

                  2.如何恢复现场

                  3.函数递归的出口

代码

class Solution {List<List<Integer>> ret=new ArrayList<>();List<Integer> path=new ArrayList<>();public List<List<Integer>> subsets(int[] nums) {dfs(nums,0);return ret;  }public void dfs(int[] nums,int i){if(i==nums.length){ret.add(new ArrayList(path));//这里不用恢复现场return;}//如果选了path.add(nums[i]);dfs(nums,i+1);//回溯 恢复现场path.remove(path.size()-1);//如果不选dfs(nums,i+1);}
}

全排列问题思路分析

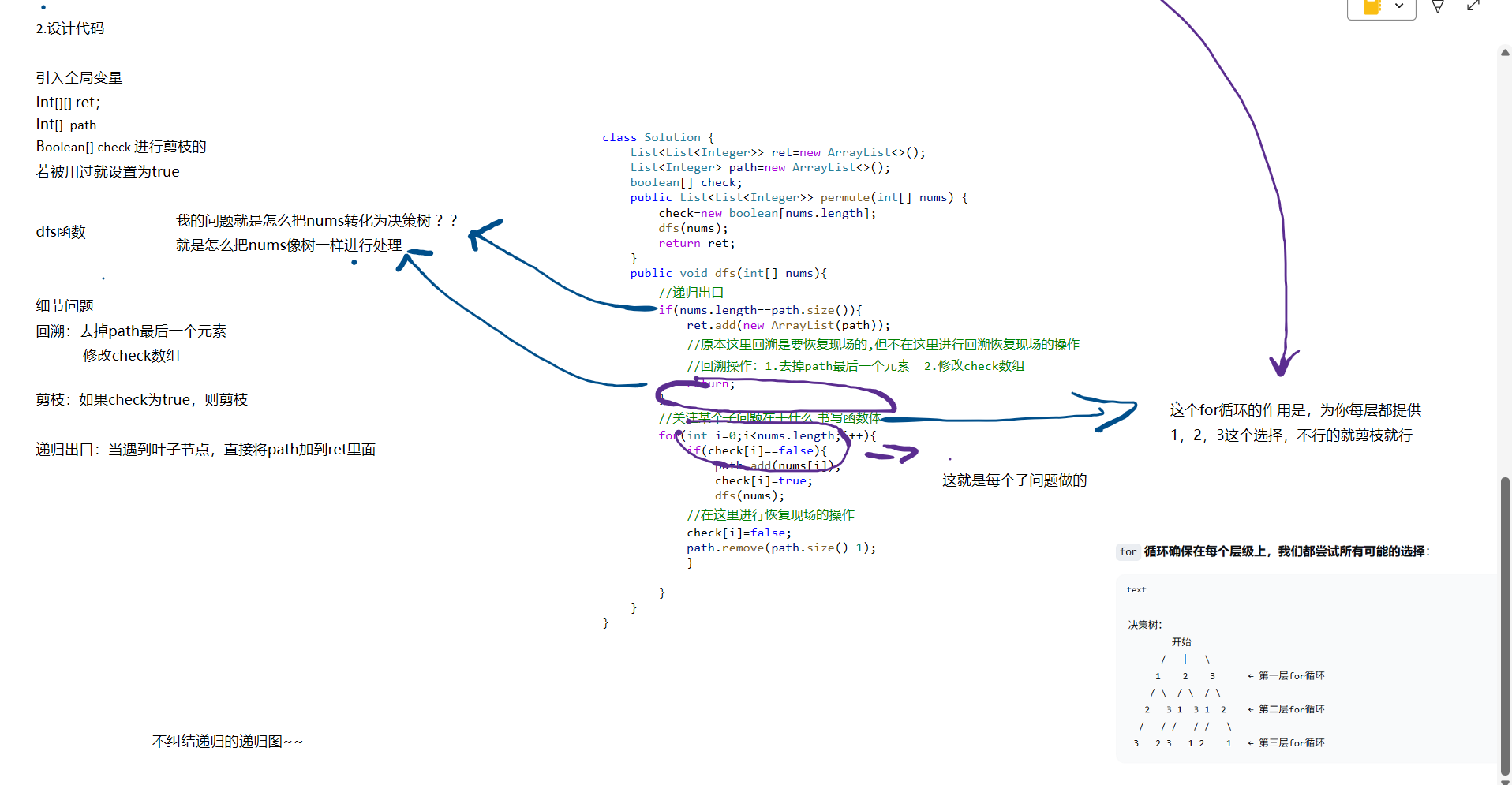
重点关注：1.引入全局变量path，ret的好处（大大简化函数头的设计）

                  2.如何恢复现场

                  3.函数递归的出口

                  4.以及如何进行剪枝操作的（主要是check数组在起作用）

代码

class Solution {List<List<Integer>> ret=new ArrayList<>();List<Integer> path=new ArrayList<>();boolean[] check;public List<List<Integer>> permute(int[] nums) {check=new boolean[nums.length];dfs(nums);return ret;}public void dfs(int[] nums){//递归出口if(nums.length==path.size()){ret.add(new ArrayList(path));//原本这里回溯是要恢复现场的,但不在这里进行回溯恢复现场的操作//回溯操作：1.去掉path最后一个元素  2.修改check数组return;}//关注某个子问题在干什么 书写函数体for(int i=0;i<nums.length;i++){if(check[i]==false){path.add(nums[i]);check[i]=true;dfs(nums);//在这里进行恢复现场的操作check[i]=false;path.remove(path.size()-1);}}}
}

总结

这两道题在我看来其实没什么差别，如果可以列举出所有情况（即画出决策树），就可以大胆地使用深度优先遍历