MIT-最大连续子序列和(MCS)
文章目录
- 问题描述
- 例子
- 算法实现
- 暴力算法
- 重用数组
- 分治算法(DC)
- 动态规划解法
问题描述
设有一家公司的历年利润记录如下:
在连续的若干年中,每一年的利润(单位:百万美元)可表示为一个序列:
P=[−3,2,1,−4,5,2,−1,3,−1]P=[-3,2,1,-4,5,2,-1,3,-1]P=[−3,2,1,−4,5,2,−1,3,−1]
问题的目标是:在该利润序列中,寻找一个连续子序列(contiguous subsequence),使得该子序列中所有元素的和达到最大值。
我们定义输入是一组数组 A[1...N]A[1...N]A[1...N]。V(i,j)V(i,j)V(i,j) 是区间 [i,j][i,j][i,j] 中所有元素的额和,其中 1≤i≤j≤n1\leq i\leq j\leq n1≤i≤j≤n ,有:
V(i,j)=∑x=ijA(x)V(i,j)=\sum_{x=i}^j A(x)V(i,j)=x=i∑jA(x)
我们的目的是找到一组索引 i≤ji\leq ji≤j,使得:
∀(i′,j′),V(i′,j′)≤V(i,j)\forall(i^{\prime},j^{\prime}),V(i^{\prime},j^{\prime})\leq V(i,j)∀(i′,j′),V(i′,j′)≤V(i,j)
例子
在上述利润序列中,若选择第 5 年至第 8 年的利润(即 [5,8][5,8][5,8] 区间),对应的子序列为 [5,2,−1,3][5,2,−1,3][5,2,−1,3]。其总利润为:
5+2−1+3=95+2-1+3=95+2−1+3=9
这是所有可能的连续年份区间中利润总和的最大值。因此,该公司在第 5 年至第 8 年期间取得了最高的累计利润 9 百万美元。
算法实现
暴力算法
首先我们想到的就是遍历所有可能的区间 (i,j)(i,j)(i,j),然后来计算每个区间的 V(i,j)V(i,j)V(i,j),从而找到最大的 V(i,j)V(i,j)V(i,j)。
int V;
int VMAX = A[1]
for (int i = 1; i <= n; i ++ )
{for (int j = i; j <= n; j ++ ){V = 0;for (int k = i; k <= j; k ++ )V += A[k];if (V > VMAX) VMAX = V;}
}
return VMAX;
时间复杂度:O(n3)O(n^3)O(n3)
重用数组
假设数组 A=[1,2,3,4,5]A=[1,2,3,4,5]A=[1,2,3,4,5]
第一个暴力算法:
- 对于 V(1,3)=A[1]+A[2]+A[3]=6V(1,3)=A[1]+A[2]+A[3]=6V(1,3)=A[1]+A[2]+A[3]=6
- 对于 V(1,4)=A[1]+A[2]+A[3]+A[4]=10V(1,4)=A[1]+A[2]+A[3]+A[4]=10V(1,4)=A[1]+A[2]+A[3]+A[4]=10
暴力算法重复计算了A[1],A[2],A[3]A[1],A[2],A[3]A[1],A[2],A[3]。而 V(1,3)=A[1]+A[2]+A[3]V(1,3)=A[1]+A[2]+A[3]V(1,3)=A[1]+A[2]+A[3],我们可以发现V(1,4)=V(1,3)+A[4]V(1,4)=V(1,3)+A[4]V(1,4)=V(1,3)+A[4]。这样不就可以大幅度的减少了计算量。
故此我们定义:
V(i,j)=∑x=ijA[x]=V(i,j−1)+A[j]V(i,j)=\sum_{x=i}^jA[x]=V(i,j-1)+A[j]V(i,j)=x=i∑jA[x]=V(i,j−1)+A[j]
int VMAX = A[1];
int V;for (int i = 1; i <= n; i ++ )
{V = 0;for (int j = i; j <= n; j ++ ){V += A[j];if (V > VMAX) VMAX = V;}
}
return VMAX;
时间复杂度:O(n2)O(n^2)O(n2)
分治算法(DC)
对于任意一个数组 A(i,j)A(i,j)A(i,j),如果我们将它从中间分成两半(中点是 M=⌊i+j2⌋M=\lfloor\frac{i+j}{2}\rfloorM=⌊2i+j⌋):
- 左半部分:A(i,M)A(i,M)A(i,M)
- 右半部分:A(M+1,j)A(M+1,j)A(M+1,j)
那么这个数组的最大连续子序列(MCS) 只可能存在于以下三种情况中:
- S1S_1S1:MCS 完全位于左半部分。
- S2S_2S2:MCS 完全位于右半部分。
- AAA:MCS 跨越了中点。这个子序列一定是由 A(i,M)A(i,M)A(i,M) 的某个后缀(包含A[M]A[M]A[M])和 A[M+1,j]A[M+1,j]A[M+1,j]的某个前缀(包含 A[M+1]A[M+1]A[M+1])拼接而成。
即最后的 最大连续子序列(MCS) 是 max(S1,S2,A)。\max(S_1,S_2,A)。max(S1,S2,A)。
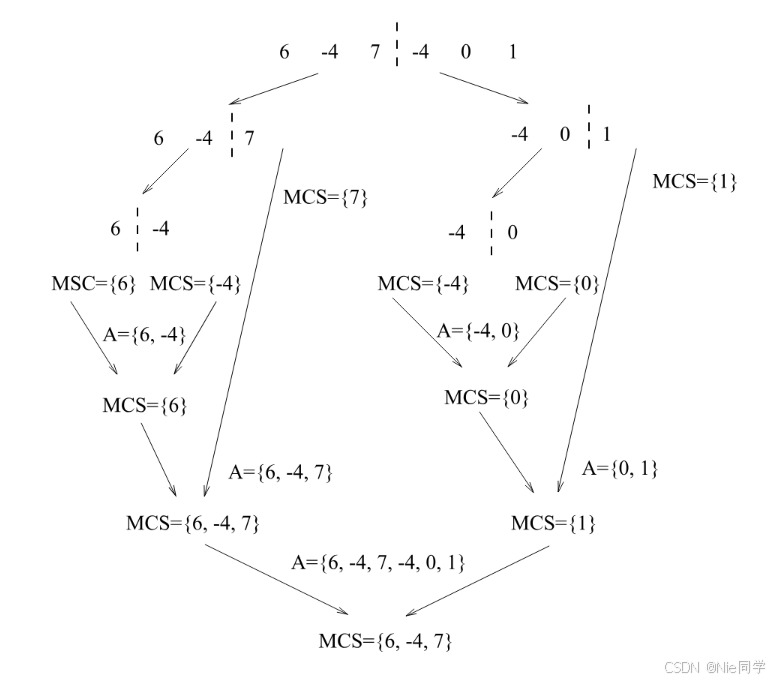
计算A的最大连续子序列(MCS):

int Find_A(int A[], int i, int j, int M)
{int A_1, A_2;int MAX = A[M];int SUM = 0;// 计算A(i,M)的最大连续子序列的某个后缀(包含A[M])for (int k = M; k >= i; k -- ){SUM += A[k];if (SUM > MAX) MAX = SUM;}A_1 = MAX;MAX = A[M + 1];SUM = 0;// 计算A(M + 1,j)的最大连续子序列的某个前缀(包含A[M + 1])for (int k = M + 1; k <= j; k ++ ){SUM += A[k];if (SUM > MAX) MAX = SUM;}A_2 = MAX;return A_1 + A_2;
}
划分与合并
int MCS(int A[], int i, int j)
{if (i == j) return A[i];int M = (i + j) / 2;int S_1 = MCS(A, i, M);int S_2 = MCS(A, M + 1, j);int A = Find_A(A, i, j, M);return MAX(S_1, S_2, A);
}
时间复杂度:O(nlog(n))O(n\log(n))O(nlog(n))
设m=j−i+1m=j-i+1m=j−i+1,T(m)T(m)T(m) 是执行 MSC(A,i,j)MSC(A,i,j)MSC(A,i,j) 所需的时间。
if (i == j) return A[i]:O(1)O(1)O(1)int M = (i + j) / 2:O(1)O(1)O(1)int S_1 = MCS(A, i, M):O(m/2)O(m/2)O(m/2)int S_2 = MCS(A, M + 1, j):O(m/2)O(m/2)O(m/2)int A = Find_A(A, i, j, M):O(m)O(m)O(m)return MAX(S_1, S_2, A):O(1)O(1)O(1)
前提条件:O(1)=T(1)O(1)=T(1)O(1)=T(1),nnn 是 2 的指数,且当 n>1n>1n>1 时有,Tn=2T(n2)+O(n)T_n=2T(\frac{n}{2})+O(n)Tn=2T(2n)+O(n)
我们一定可以找到一个常数 ccc ,使得 T(n)≤2T(n2)+cnT(n)\leq 2T(\frac{n}{2})+cnT(n)≤2T(2n)+cn
Tn≤2T(n2)+cn≤2[2T(n22)+cn2]+cn=22T(n22)+2cn≤22[2T(n23)+cn22]+2cn=23T(n23)+3cn≤...=2hT(n2h)+hcn\begin{aligned} T_n&\leq2T(\frac{n}{2})+cn \\&\leq 2\left[2T\left(\frac{n}{2^{2}}\right)+c\frac{n}{2}\right]+cn \\ & = 2^2T\left(\frac{n}{2^2}\right)+2cn \\ & \leq2^2\left[2T\left(\frac{n}{2^3}\right)+c\frac{n}{2^2}\right]+2cn \\ & = 2^3T\left(\frac{n}{2^3}\right)+3cn \\ & \leq ... \\& = 2^hT\left(\frac{n}{2^h}\right)+hcn \end{aligned}Tn≤2T(2n)+cn≤2[2T(22n)+c2n]+cn=22T(22n)+2cn≤22[2T(23n)+c22n]+2cn=23T(23n)+3cn≤...=2hT(2hn)+hcn
我们令 h=log2nh=\log_2nh=log2n,所以 n=2hn=2^hn=2h,有:
T(n)≤nT(1)+cn(log2n)=O(n)+cnlog2n=O(nlog2n)T(n)\leq nT(1) + cn(\log_2n)=O(n) + cn\log_2n=O(n\log_2n)T(n)≤nT(1)+cn(log2n)=O(n)+cnlog2n=O(nlog2n)
动态规划解法
-
定义状态:
- 设
dp[i]表示以第i个元素结尾的最大子序列和。 - 目标是找到所有
dp[i]的最大值,这个最大值即为整个数列中的最大连续子序列和。
- 设
-
状态转移:
- 对于每个元素
A[i],我们可以选择将它加入前面的子序列,或者从A[i]开始新的子序列。 - 公式为:
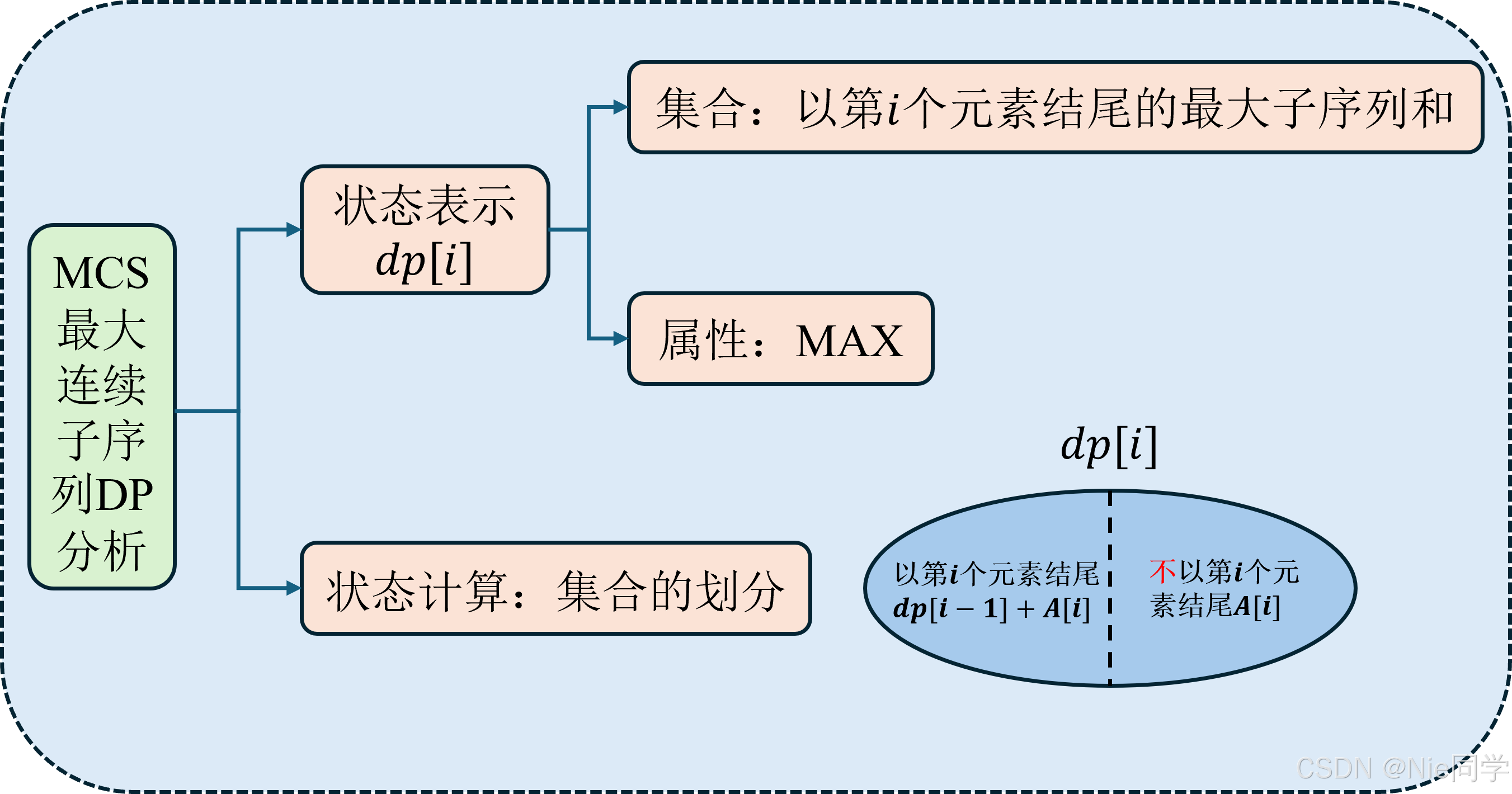
dp[i]=max(dp[i−1]+A[i],A[i])dp[i]=\max(dp[i-1]+A[i],A[i])dp[i]=max(dp[i−1]+A[i],A[i])
这表示我们要么把A[i]加到之前的最大和(即继续前面的子序列),要么从A[i]开始一个新的子序列。
- 对于每个元素
max_sum = A[1];
dp[1] = A[1];
for (int i = 2; i <= n; i ++ )
{dp[i] = max(dp[i - 1] + A[i], A[i]);max_sum = max(max_sum, dp[i])
}return max_sum;
时间复杂度:O(n)O(n)O(n)
