砂轮姿态调整的几何艺术：摆角与抬角变换的数学原理

在钻尖后刀面磨削工艺中，砂轮位姿的精确控制是保证加工质量的核心。当砂轮的初始姿态确定后，实际磨削过程中还需要进行精细的姿态调整，这就是摆角变换与抬角变换的几何意义所在。这两种变换不仅是避免干涉的技术手段，更是控制后刀面几何形状的精妙艺术。

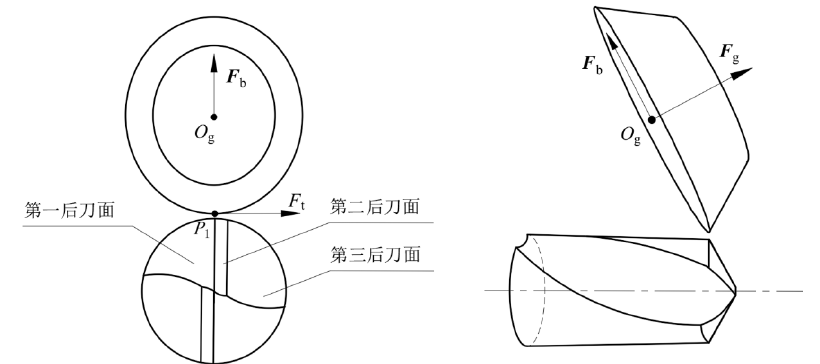
从理想到现实：姿态调整的必要性

砂轮的初始磨削姿态建立在理想化的几何假设之上——砂轮大端平面与钻尖圆锥面母线完美相切。然而，真实的加工环境要复杂得多。钻尖结构紧凑，后刀面、端刃、圆锥面等特征相互交错，砂轮在运动过程中极易与这些非加工区域发生碰撞。此外，钻尖后刀面并非简单的平面，而是需要特定曲率的复杂曲面，仅靠初始姿态无法满足这些精度要求。

摆角($\mu$)和抬角($\delta$)的引入，正是为了解决这些实际问题。它们为砂轮提供了额外的运动自由度，使其能够在避免干涉的同时，精确地磨削出所需的曲面形状。这种思路体现了工程实践中从理想模型到现实应用的智慧过渡。

摆角变换：砂轮的"水平微调"

摆角变换的本质是让砂轮绕自身轴线旋转一个角度，这类似于人站立时左右摇头的动作。从几何角度看，这是一种刚体绕定轴旋转的运动。

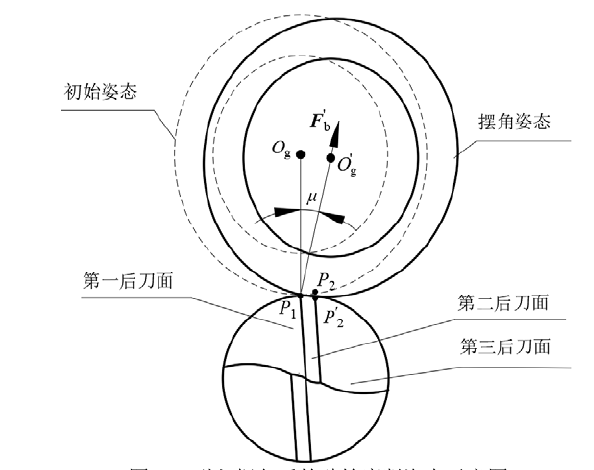
数学上，我们使用旋转矩阵来描述这种变换。 对于绕任意单位矢量$N$旋转角度$\eta$的变换，其齐次坐标下的变换矩阵为：

$$Rot(N,\eta )=\left[\begin{array}{cccc}{N}_x{N}_x\text{vers}\eta +\cos \eta & N_x{N}_y\text{vers}\eta -N_z\sin \eta & N_x{N}_z\text{vers}\eta +N_y\sin \eta & 0\\ N_y{N}_x\text{vers}\eta +N_z\sin \eta & N_y{N}_y\text{vers}\eta +\cos \eta & N_y{N}_z\text{vers}\eta -N_x\sin \eta & 0\\ N_z{N}_x\text{vers}\eta -N_y\sin \eta & N_z{N}_y\text{vers}\eta +N_x\sin \eta & N_z{N}_z\text{vers}\eta +\cos \eta & 0\\ 0& 0& 0& 1\end{array}\right]$$

其中$\text{vers}\eta =1-\cos \eta$。这个看似复杂的矩阵实际上有着清晰的几何意义：它将旋转分解为矢量投影和垂直分量的组合，确保旋转后的矢量长度保持不变。

在摆角变换中，旋转轴就是砂轮自身的轴矢量$F_g$。 这意味着砂轮绕着自己中心轴旋转角度$\mu$。这种旋转有一个重要特性：砂轮轴矢量$F_g$在变换前后保持不变，因为绕自身轴旋转不会改变轴的方向。

然而，其他相关的几何要素会发生显著变化。磨削点$P_1$的新位置通过旋转矩阵计算：

$$P_1^{\prime }=Rot(F_g,\mu )\cdot P_1$$

更重要的是，从磨削点指向砂轮圆心的矢量$F_b$也会随之旋转：

$$F_b^{\prime }=Rot(F_g,\mu )\cdot F_b$$

这种变换的物理效果十分精妙。 由于$F_b$的方向改变，砂轮圆心的实际位置也随之移动。新的圆心位置为：

$$O_g^{\prime }=P_1^{\prime }+R_g\cdot F_b^{\prime }$$

其中$R_g$是砂轮半径。这就意味着，虽然砂轮的"朝向"没有变，但它的整体位置发生了水平方向的偏移，恰好能够避开可能发生碰撞的区域。这种调整就像是在拥挤的空间中侧身通过，既保持了身体方向，又避免了触碰。

抬角变换：砂轮的"垂直精修"

如果说摆角变换解决了水平方向的干涉问题，那么抬角变换则专注于垂直方向的形状控制。抬角变换让砂轮绕着切矢$F_l$旋转角度$\delta$，这类似于人站立时的点头动作。

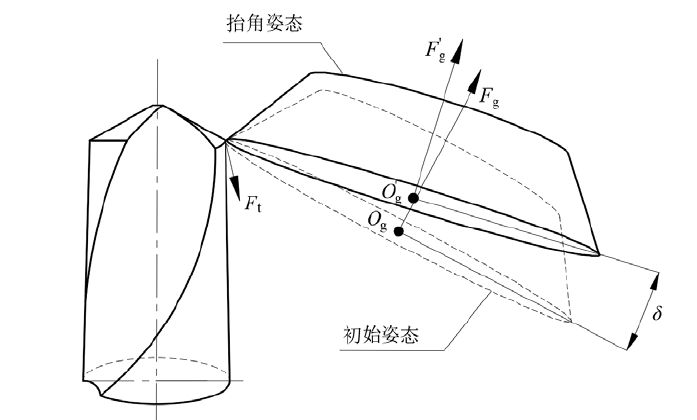
从几何学角度看，抬角变换改变了砂轮与工件的相对角度。 切矢$F_l$是砂轮在磨削点处的切线方向，由法矢$F_p$与砂轮轴矢量$F_g$的叉积决定：

$$F_l=F_p\times F_g$$

选择切矢作为旋转轴具有深刻的几何意义。这样一来，砂轮的旋转轴恰好沿着磨削点的切线方向，使得砂轮能够以最自然的方式调整其与工件表面的接触角度。

抬角变换的数学表达同样基于旋转矩阵：

砂轮轴矢量的新方向为：
$$F_g^{\prime \prime }=Rot(F_l,\delta )\cdot F_g$$

矢量$F_b^{\prime }$的新方向为：
$$F_b^{\prime \prime }=Rot(F_l,\delta )\cdot F_b^{\prime }$$

最终的砂轮圆心位置为：
$$O_g^{\prime \prime }=P_1^{\prime }+R_s\cdot F_b^{\prime \prime }$$

抬角变换的工艺效果极为重要。 当$\delta =0$时，砂轮以大端平面进行磨削，产生的是近似平面的后刀面。随着$\delta$角的增大，砂轮逐渐从端面磨削过渡到圆周面磨削，能够加工出复杂的曲面后刀面。这种转变不仅影响了后刀面的形状，还改变了切屑流出的空间和刀具的散热性能，直接影响钻头的切削性能。

变换的协同效应：一加一大于二

摆角与抬角变换虽然可以单独分析，但在实际应用中它们共同作用，产生协同效应。变换的顺序也很有讲究：先进行摆角变换，再进行抬角变换。这种顺序保证了变换的层次性和可控性。

从数学上看，这是一个复合变换过程。 砂轮的最终位姿是初始位姿经过两次连续旋转的结果。在矩阵运算中，这种复合变换表现为矩阵的连乘：

$$F_g^{\prime \prime }=Rot(F_l,\delta )\cdot [Rot(F_g,\mu )\cdot F_g]$$

由于矩阵乘法不满足交换律，变换顺序的不同会导致完全不同的结果。先摆角后抬角的顺序在实践中被证明是最有效的，因为它先解决干涉问题，再处理形状精度，符合工艺优化的逻辑。

这种复合变换的几何意义可以理解为在球面上的运动。 砂轮的取向变化可以看作是在单位球面上点的移动：摆角变换相当于沿着纬线移动，抬角变换相当于沿着经线移动。两个自由度的组合使得砂轮能够到达球面上的任意点，即能够实现任何需要的取向。

工程实践中的参数优化

摆角$\mu$和抬角$\delta$的具体数值需要通过优化确定。过小的角度可能无法有效避免干涉或达不到形状要求，过大的角度又可能导致磨削力分布不均或砂轮强度问题。

在实践中，这些参数的确定往往基于以下考虑：

• 通过几何分析确定避免干涉的最小必要角度
• 根据后刀面的设计曲率计算所需的抬角范围
• 考虑砂轮的刚性磨损特性确定安全的工作范围
• 通过实验验证优化最终的参数选择

这种参数优化过程体现了理论计算与工程经验的完美结合。数学公式提供了基础框架，而实践经验则赋予这个框架以生命力。

结语：几何之美与工艺之精

砂轮的摆角与抬角变换，表面上看是简单的旋转运动，深层次却蕴含着丰富的几何原理和工艺智慧。通过这些变换，我们能够将简单的砂轮运动转化为复杂的曲面创成过程，将抽象的数学计算转化为实在的加工精度。

这种从几何定义到工艺实现的转换，体现了制造技术的精髓：用严谨的数学语言描述复杂的物理过程，用简洁的几何变换解决棘手的工程问题。在这个过程中，摆角和抬角不仅是两个角度参数，更是连接设计与制造、理想与现实的桥梁。

正是这种对几何关系的深刻理解和对工艺需求的敏锐把握，使得钻尖磨削从一门技艺上升为一门科学，展现了人类智慧在解决复杂工程问题时的创造力和精确性。