算法20.0
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
目录
一、查找区间左端点
1.0 自己的理解
2.0 细节
3.0 别人的理解
(1)解法:
(2)细节处理: 循环条件和求中点操作 编辑
二、查找区间右端点
1.0 自己的理解
2.0 细节
3.0 别人的理解
一、查找区间左端点
1.0 自己的理解
为什么朴素二分法在这道题目时间复杂度很高?
朴素二分法能找到那个数字 但是不知道是第几个 需要向两边扩散
此时最好的情况是目标值唯一 最坏的情况是目标值占满整个数组(3,3,3,3,3,3,3,3,3),此时需要遍历全部数 这样的话时间复杂度很高 极端情况下会超时 不推荐
查找区间左端点的时候 为什么分情况是小于一种 大于和等于一种 以及此时的结果情况是?
因为这个和朴素二分法不一样 此时的大于和等于不能分情况讨论了
找到的这个元素小于t可以确保左面那个区间扔了 然后left移动到mid+1
但是找到的这个元素等于 不一定这个元素就是要找的左端点 但是可以确保这个元素的右面一定有要找的右端点 更新的话不能让right直接到mid-1了(这时的mid有可能是最终结果) 要让right = mid
为什么循环条件是left<right 而不是left<=right ?
left的更新是mid+1 它一直想要跳出来 到mid右边
right的更新是mid 没有想要出来也出不来 一直是靠近mid最后成为mid
它们两个相遇的场景就是 就是最终找到的那个结果 无需判断
为什么left=right的时候判断 就会死循环?
因为right不动(right=mid) left也不动 它们卡在那里一直循环(看星星标记下的2号情况)
为什么求中点操作只能用 left+(right-left)/2呢?
如果数组是奇数个的话 求得的中点只能是中间那个点
但是如果数组是偶数个的话 求中点的两个表达式 是不一样的结果 一个靠左的中点一个靠右的中点 在朴素二分法的时候都是可以的 但是这里不行
当最后一次操作的时候 数组里面只剩下两个元素
用第二种方法求中点 mid落在右面那个 如果最后的判断中了星号的第一个条件
left到mid后面+1 超出去了 程序是会结束的
如果中了星号的第二个条件 x>=t right=mid 下一步进入循环求中点的时候还是right到mid 死循环了
2.0 细节
审题:
//非递减:要么增要么不动 用图形化来表示是下面的样子

//题目最后给了特殊情况 如果是空的数组 我们返回-1就可以了 这个部分也是做题的一种情况
3.0 别人的理解
(1)解法:
暴力解法 从前面往后遍历 然后返回
尝试使用朴素的二分算法解决问题 发现有问题
尝试优化朴素二分法:二分的本质是二段性 要找到题目里的二段性

查找区间左端点的时候 发现了二段性
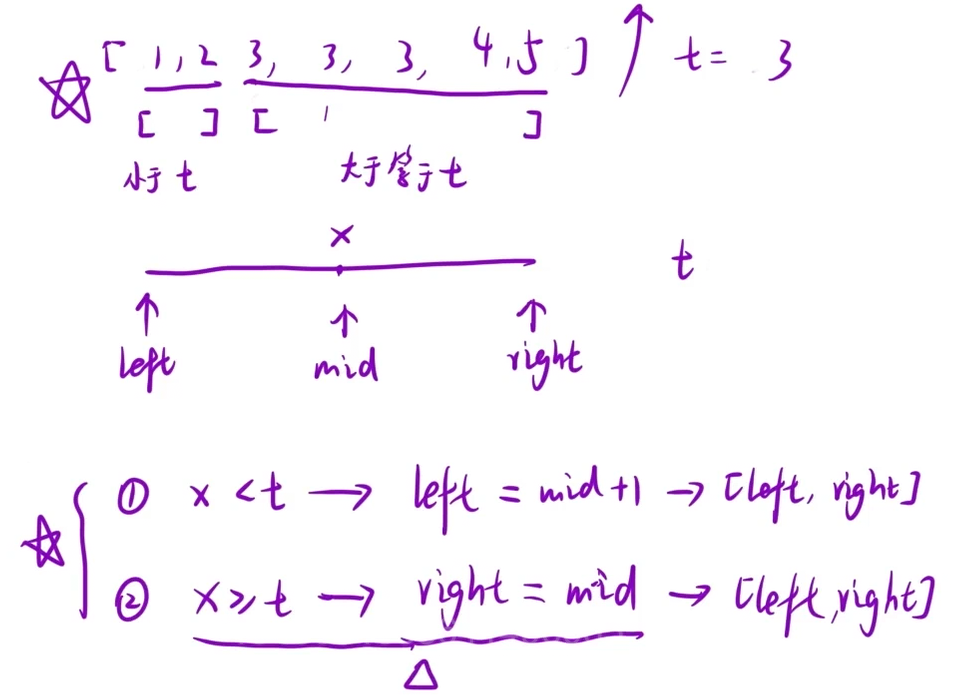
(x表示mid位置的值)
(2)细节处理: 循环条件和求中点操作

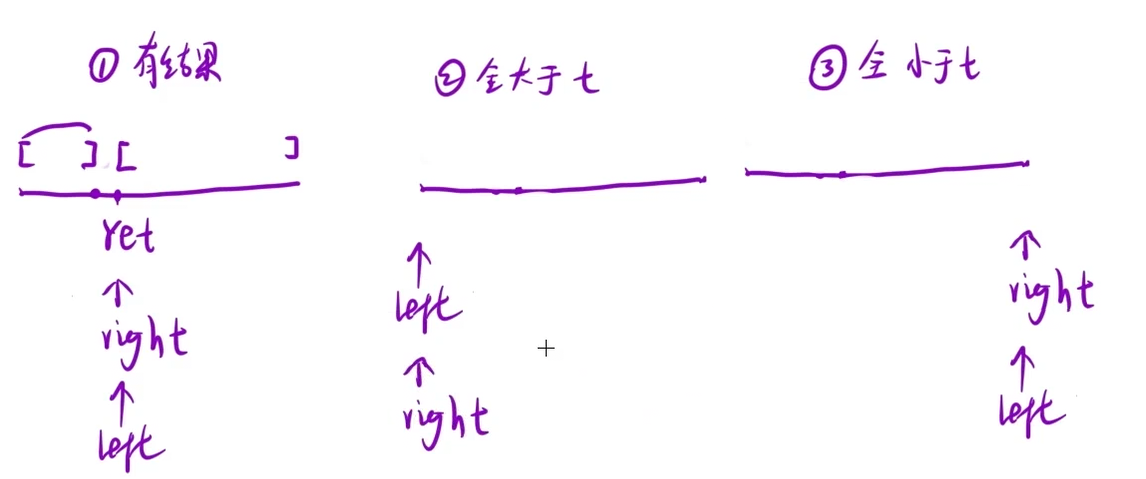
求中点操作
防溢出 left+(right-left)/2 可以
left +(right-left+1)/2不行

二、查找区间右端点
和查找区间左端点的思路相同 但是有的地方细节不同
1.0 自己的理解
查找右区间端点 x<=t的时候 为什么是left=mid?
left不能越过去 因为越过的这个元素可能正是我们要找到元素
right的更新策略为什么是right=mid-1?
mid落在的区间一定是不符合要求的(就像是查找左区间 left一定想要跳出来 那个区间就没有 这里也一样 right也一直想要跳出这个区间 因为这个区间没有要找的点)
2.0 细节
3.0 别人的理解


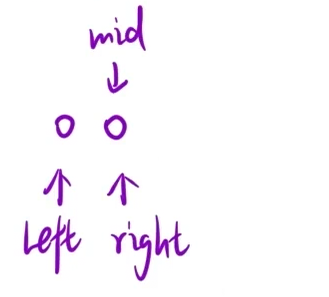
插播一个二分模板

下面是题目、效果图和代码:
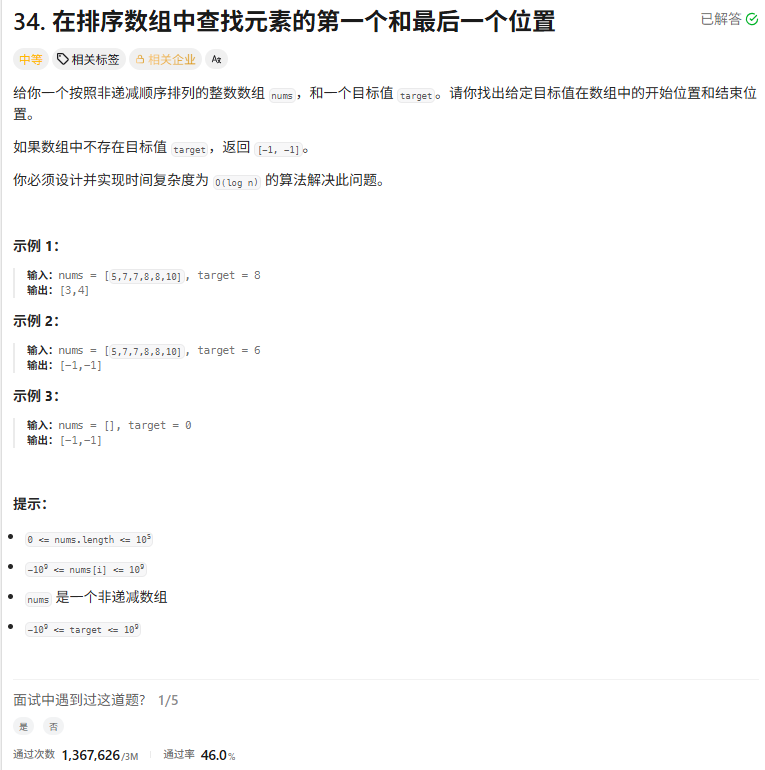
class Solution {public int[] searchRange(int[] nums, int target) {//处理边界情况int[] ret = new int[2];ret[0] = ret[1] = -1;if(nums.length == 0 ) return ret;//1.二分左端点int left = 0 , right = nums.length-1;while(left<right){int mid = left+(right-left)/2;if(nums[mid]<target) left = mid +1;else right = mid;}//因为这个数组有可能有没有target 所以需要判断一下//判断是否有结果if(nums[left] != target) return ret;else ret[0]=right;//2.二分右面端点left = 0 ;right = nums.length-1;//因为已经找到区间的左端点 不需要从0开始 我们此时可以从左端点开始while(left<right){int mid = left+(right-left+1)/2;if(nums[mid]<=target) left = mid;else right = mid-1;}ret[1]=left;return ret;}
}
//xiyu251030&1#3*2
