【自适应PF例程】基于Sage Husa的自适应粒子滤波与经典PF对比，MATLAB编写，可直接运行。三维状态量，非线性的状态与观测。附代码下载链接

标准粒子滤波（Particle Filter, PF）与基于 Sage–Husa 自适应估计的自适应粒子滤波（Adaptive Particle Filter, APF）在三维非线性系统下的性能对比。

代码简介

程序展示了**标准粒子滤波（Particle Filter, PF）与基于 Sage–Husa 自适应估计的自适应粒子滤波（Adaptive Particle Filter, APF）**在三维非线性系统中的对比效果。
算法以非线性状态和观测模型为背景，通过随机粒子采样、似然权重更新和重采样机制，实现对目标状态的动态估计。APF 在此基础上进一步引入自适应噪声估计机制，能够在未知或变化的环境下自动调整滤波参数，从而获得更加稳定、精确的估计结果。

算法亮点

• 对比：在同一非线性系统下，PF 使用固定噪声参数，而 APF 能自动调整噪声强度，实时响应环境变化。
• 自适应噪声学习：APF 借鉴 Sage–Husa 思想，根据滤波过程中观测到的新息信息动态更新噪声统计，实现自学习与自校正。
• 非线性系统适用性强：无需线性化，适用于复杂状态变化和非高斯噪声环境。

结果展示

程序绘制了以下多组结果图与统计指标：

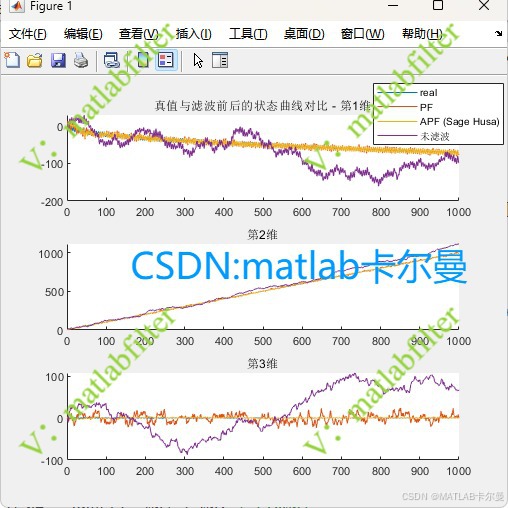
• 三维状态的真值、PF 与 APF 滤波轨迹对比；
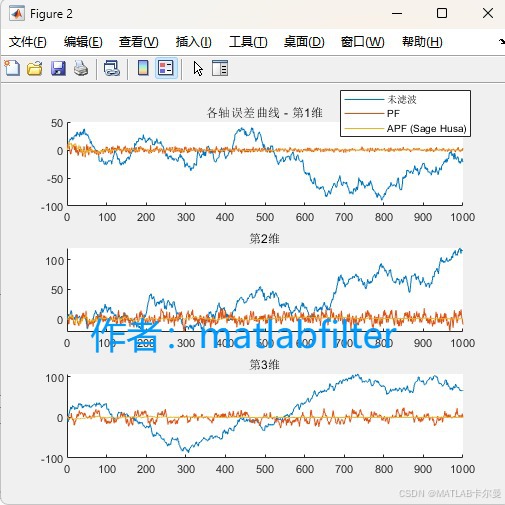
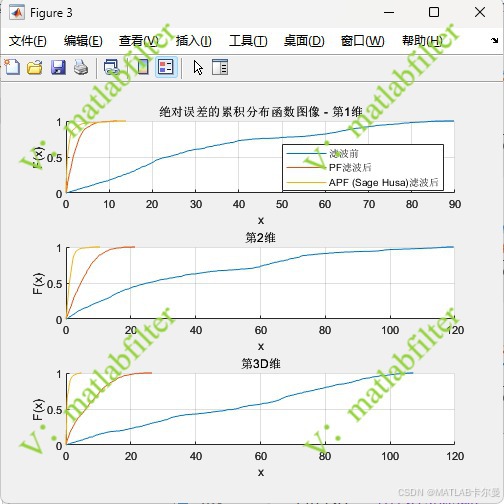
• 各维度的误差变化曲线与累积分布曲线；
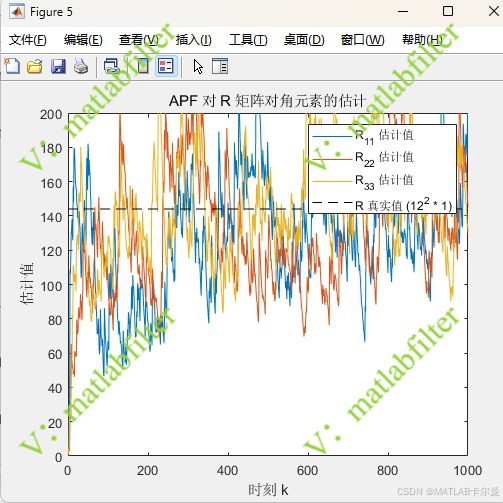
• 自适应滤波器对真实噪声强度的学习过程；
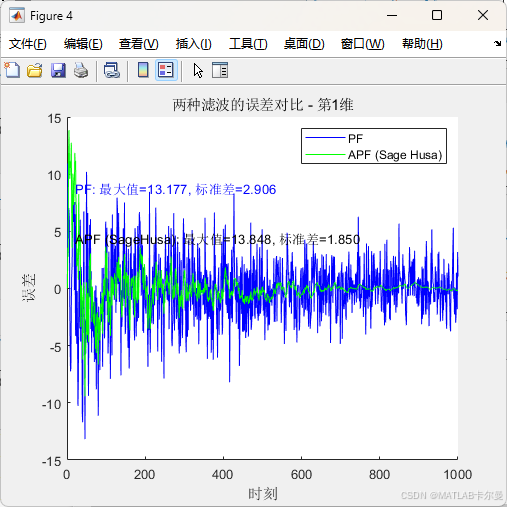
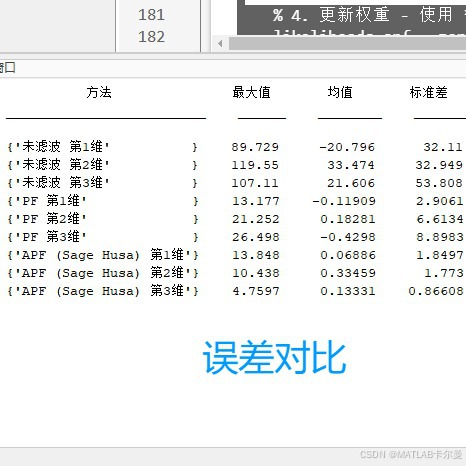
• 各算法的最大误差、均值和标准差对比表格。

结果显示，标准 PF 在噪声假设错误时性能下降明显，而 APF 能自动修正噪声估计，使误差分布更集中、收敛更平稳，表现出更强的鲁棒性和自适应能力。

运行结果

三维状态曲线对比：

误差对比：

误差CDF对比：

第一维误差指标：

命令行窗口输出的误差特性对比：

R的自适应估计曲线：

MATLAB源代码

部分代码如下：

% PF / APF 三维滤波，APF基于SageHusa思想自适应调节QR
% 作者:matlabfilter
% 2025-10-19/Ver2 (由 EKF/AEKF 修改为 PF/APF)
clear; clc; close all;% 清除变量、命令行和图形窗口
rng(0); % 设置随机数种子%% 滤波模型初始化
t = 1:1:1000;
n = 3;  % 三维
T = length(t);
Q = 10 * diag([1,1,1]);      % 真正的过程噪声协方差（三维）
R = 1 * diag([1,1,1]);       % 滤波器*初始*假定的观测噪声协方差（三维）
% 注意：下面生成观测值时，故意使用了一个被12倍缩放的噪声
% 实际的观测噪声协方差
R_real = 144 * R;
% 自适应滤波的目的就是去估计这个 R_realNp = 500; % 粒子数 (PF/APF)% 用 cholesky 生成噪声序列
w = 1*chol(Q)' * randn(n, T);   % 过程噪声
v_raw = 1*chol(R)' * randn(n, T);   % 原始观测噪声
P0 = 1 * eye(n);X = zeros(n, T);
X_pf = zeros(n, T);  % PF 声明变量
X_apf = zeros(n, T); % APF 状态 声明变量
Z = zeros(n, T);Z(:,1) = [0;0;0] + v_raw(:,1); % 三维初值% 预分配用于存储 (APF)
Q_num = zeros(n,n,T); Q_num(:,:,1) = Q;
R_num = zeros(n,n,T); R_num(:,:,1) = R;
% P_num 不再需要，粒子滤波没有P矩阵% APF (Sage-Husa) 初始为矩阵形式
Q_sh = Q;
R_sh = R;% 遗忘因子
b = 0.95;
eps_min = 1e-6;  % 用于保持正定%% 运动模型（三维）
X_ = zeros(3, length(t)); % 给带误差的（未滤波的）状态量建立空间
X_(:, 1) = X(:, 1); % 给带误差的状态量赋初值for i1 = 2:length(t)% 真实状态更新（三维非线性模型）X(:, i1) = [X(1, i1-1) + (2.5 * X(1, i1-1) / (1 + X(1, i1-1)^2)) + 8 * cos(1.2 * (i1-1));X(2, i1-1) + 1;X(3, i1-1) + 0.5 * sin(0.8 * (i1-1))];  % 第三维加入正弦变化% 未滤波状态更新X_(:, i1) = [X_(1, i1-1) + (2.5 * X_(1, i1-1) / (1 + X_(1, i1-1)^2)) + 8 * cos(1.2 * (i1-1));X_(2, i1-1) + 1;X_(3, i1-1) + 0.5 * sin(0.8 * (i1-1))] + w(:, i1-1);% 观测值更新（三维观测模型）Z(:, i1) = [X(1, i1)^2 / 20; X(2, i1); X(3, i1)^2 / 30] + sqrt(diag(R_real)).*v_raw(:,i1); % 构造噪声不确定
endX_pf(:, 1) = X_(:, 1);  % PF 估计值的初值
X_apf(:, 1) = X_(:, 1); % APF 估计值的初值% === PF / APF 初始化粒子 ===
% 从初始估计 X_(:, 1) 和 P0 采样

代码下载链接：
https://download.csdn.net/download/callmeup/92204975

更多完整的代码，可查看专栏文章：
https://blog.csdn.net/callmeup/article/details/153920147?sharetype=blogdetail&sharerId=153920147&sharerefer=PC&sharesource=callmeup&spm=1011.2480.3001.8118

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者