第三章 线性模型
一、基本思想
定义:线性模型试图通过属性的线性组合进行预测:
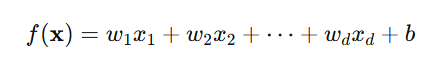
或向量形式:
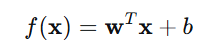
特点:
形式简单、可解释性强(权重 wi表示属性重要性)
许多非线性模型可在线性模型基础上引入层级结构或高维映射得到

二、线性回归
目标:预测实值输出标记
单变量情形:
使用最小二乘法求解 w 和 b
多变量情形:
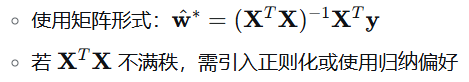
- 广义线性模型:


三、对数几率回归(逻辑回归):做分类
用途:二分类任务
核心思想:用对数几率函数(Sigmoid)将线性输出映射到 (0,1)(0,1):
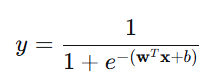
优势:
直接对分类概率建模
输出具有概率意义
是凸函数,易于优化
参数估计:使用极大似然估计,通过梯度下降或牛顿法求解

四、线性判别分析(LDA):找最佳投影线

思想:将样本投影到一条直线上,使得:
同类样本的投影点尽可能接近
异类样本的投影点尽可能远离
目标函数(广义瑞利商):
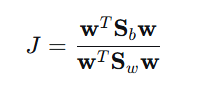

多分类推广:可扩展到多分类任务,并可用于监督降维
五、多分类学习策略
基本思路:将多分类任务拆解为多个二分类任务
三种经典策略:
OvO(一对一):训练 N(N−1)/2N(N−1)/2 个分类器,通过投票决定类别
OvR(一对其余):训练 NN 个分类器,选择置信度最高的
MvM(多对多):如ECOC(纠错输出码),通过编码与解码容错


3. 多对多(MvM)
通俗解释:OvO和OvR都比较“极端”——要么是1v1,要么是1v全部。而MvM(RvR)则更加灵活:每次将一部分类别划为“正队”,另一部分类别划为“反队”,让这两个队伍进行PK。
核心步骤:
编码:设计多轮团队对抗赛。每一轮,都按照一个规则把3个类别分成“正队”和“反队”,训练一个分类器。
解码:一个新样本(新瓜)来的时候,让它参加所有这些“比赛”,看它在每一轮中被分到了“正队”还是“反队”,从而得到一个由(+1, -1)组成的“身份编码”。最后,看这个编码最像哪个类别的预设编码。
总结与对比
| 策略 | 形象比喻 | 核心思想 | 优点 | 缺点 |
|---|---|---|---|---|
| OvO(一对一) | 循环单挑赛 | 两两配对,训练多个分类器 | 训练每个分类器只用两类数据,相对简单 | 分类器数量多(N(N-1)/2) |
| OvR(一对其余) | 海选+总决赛 | 一个类别 vs 其余所有类别 | 分类器数量少(N个) | 每个分类器训练数据不均衡,训练难度大 |
| MvM(多对多) | 团队对抗赛 | 部分类别 vs 另一部分类别 | 设计灵活,有纠错能力 | 编码设计复杂,需要专业知识 |
六、类别不平衡问题

问题:不同类别的训练样本数差异大,导致模型偏向多数类
解决方法:
再缩放:调整决策阈值
欠采样:减少多数类样本
过采样:增加少数类样本(如SMOTE)
阈值移动:在决策过程中嵌入再缩放
与代价敏感学习的关系:将再缩放中的样本比例替换为误分类代价
