加法器进位的那些事

目录

一、前言

二、十进制的加法

三、 二进制的加法

四、分组进位

---

一、前言

你知道二进制吗？ 你了解他的加法进位吗？对于二进制的进位， 是怎么进位的？ 对于打位宽的加法又是怎么让其加速进位的？

---

二、十进制的加法

在日常生活中， 加法于我们无时不在， 例如 198 + 182 = ？

首先先计算个位， 然后将进位 “1” 到十位， 然后计算十位， 将进位 “1” 到百位。

---

三、 二进制的加法

在二进制的世界中， 它也是如此， 例如 A = 100110， B = 011011， A + B = ？

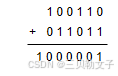
它的计算公式为：

其中，  代表第 i 位的和结果，  代表第 i 位需要往前进位的结果。

那怎么解读这个公式呢？

 比较好理解， 因为根据真值表可以得到；

 公式由两部分组成：

•   ：这个代表当前第 i 位 本身是否能进位，假设  和  都为 1， 那么  就为 1， 它肯定是要进位的；
• ：这个代表是否要传播前一位的进位 ；

非常好理解， 打个比方， 假设 A = 100110， B = 011011：

• 对于第 0 位 是否要进位取决于 ;
• 对于第 1 位 是否要进位取决于 ， 因为这里的  本身就等于 1 了， 所以是会进位；
• 对于第 2 位 是否要进位取决于， 因为这里的 本身就等于 0， 所以自身不会产生进位， 然后看后面部分 ， 因为  等于 1， 所以会将前面的  往下传播。
• 以此类推...

我们令：

那么有：

我们先看每一位 ：

每一位  都会依赖第 i 位本身是否产生进位， 如果没有就会依赖上一级是否有进位传播进来， 如果没有则会依赖上上级是否有进位传播进来， 以此类推。。。

---

四、分组进位

上面我们给出了对操作数的每一个 bit 进行进位计算， 这一章节我们来了解对于大位宽的分组进位，众所周知， 我们再搭建电路的时候为了它能够加快延时， 我们对大位宽的加法的操作数进行了分组，例如 16 位的加法：A = 1101100011110101， B = 0110110111101100.

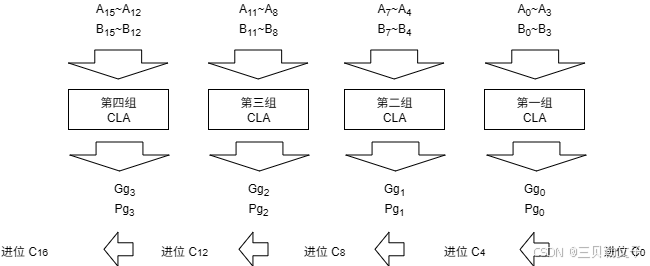
我们可以将 A 和 B 分为 4 组， 每一组就只有 4 个 bit， 我们可以计算每一组的进位， 然后将进位传播到下一组作为下一组的 “  ”， 步骤如下：

分组： 将 A 和 B 分为 4 组， 得到:

计算每一组的 “组生成项 Pg” 和 “组传播项 Gg”， Pg 类似于当前组号 j 的 , 也就是向前是否向前传播前一组的进位；Gg 类似于当前组号 j 的 ， 也就是当前组本身是否能产生进位。

那每一组的 Gg 和 Pg 怎么计算得到呢？

第一组来看， Gg 是组本身是否会产生进位， Pg 是组是否会传播组前的进位 

从第二组看， Gg 是第二组本身是否会产生进位， Pg 是第二组是否会传播第一组的进位 

从第三组看， Gg 是第三组本身是否会产生进位， Pg 是第三组是否会传播第二组的进位 

从第四组看， Gg 是第四组本身是否会产生进位， Pg 是第四组是否会传播第三组的进位 

因此每个组可以先计算  和， 最后在计算将每个组的进位往下一组传播， 这样可以节省电路的延时， 如图所示：

因为每一个组内都已经有对其他的  进行了计算， 所以很容易得到每一位的 Sum。