数据结构——三十一、最小生成树(王道408)

前言

本文介绍了最小生成树（MST）的概念及其求解方法。生成树是包含图中所有顶点的极小连通子图，边数为顶点数减1。最小生成树是权值之和最小的生成树，可能不唯一但总权值唯一。文章重点讲解了Prim算法的实现步骤：从初始顶点出发，逐步选择权值最小的边将新顶点纳入生成树，直到所有顶点都被包含。算法通过维护lowCost数组记录各顶点到生成树的最小代价，并不断更新该数组来实现最小生成树的构建。适用于带权连通无向图的最小生成树求解。

代码在文章开头,需要自取🧐

一.知识回顾:生成树

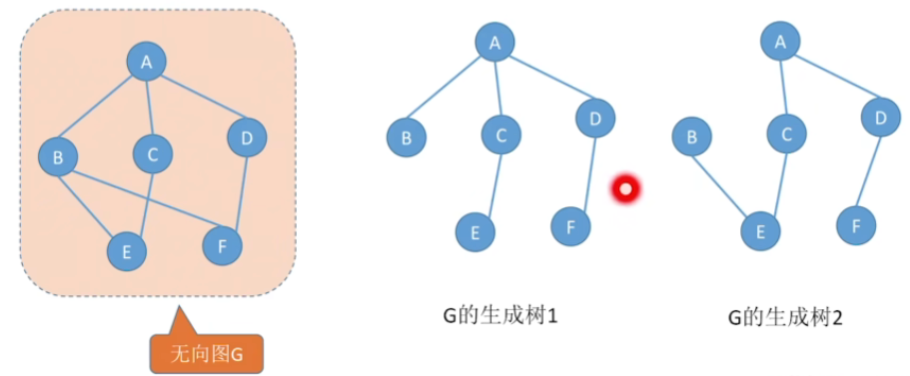
• 连通图的生成树是包含图中全部顶点的一个极小连通子图。(边尽可能的少，但要保持连通)
• 若图中顶点数为n，则它的生成树含有n-1条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。

二.最小生成树（最小代价树）

1.定义

1.专业定义

• 对于一个带权连通无向图G=(V,E)，生成树不同，每棵树的权（即树中所有边上的权值之和）也可能不同。设R为G的所有生成树的集合，若T为R中边的权值之和最小的生成树，则T称为G的最小生成树(Minimum-Spanning-Tree,MST).

2.通俗理解

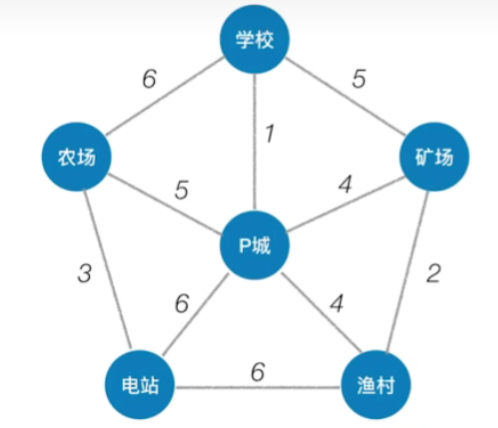
• 一个带权的连通图,它有可能会有多个生成树,我们要从它所有的这些生成树当中找出各边的权值之和最小的那一颗

2.最小生成树的特点

• 最小生成树可能有多个，但边的权值之和总是唯一且最小的

• 最小生成树的边数 = 顶点数 - 1。砍掉一条则不连通，增加一条边则会出现回路

• 如果一个连通图本身就是一棵树，则其最小生成树就是它本身
  

• 只有连通图才有生成树，非连通图只有生成森林
  

三.求最小生成树

1.Prim算法(普里姆)

1.方法

• 从某一个顶点开始构建生成树,每次将代价(权值)最小的新顶点纳入生成树，直到所有顶点都纳入为止。

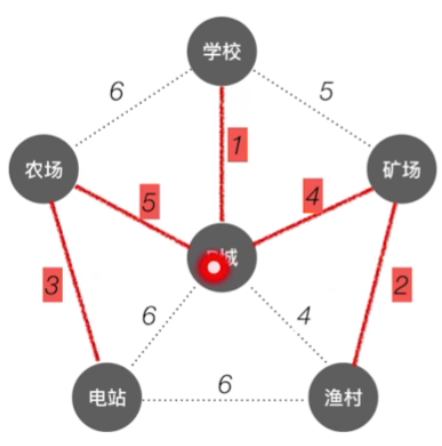
2.例子

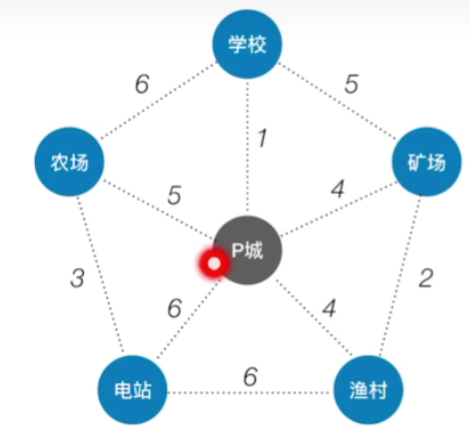
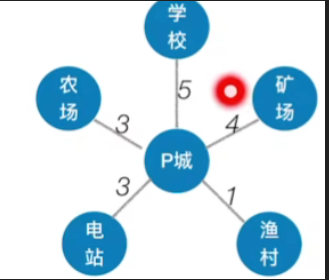
1. 如果我们从P城这个顶点开始,现在我们要构建的这颗生成树里,暂时只有p城这个顶点,如果我们把学校这个新顶点连到这个生成树里面,那我们需要花费的代价只有1,是P城的所有边里拥有最小的代价的边,因此接下来我们要把学校给并到这个生成树里
   

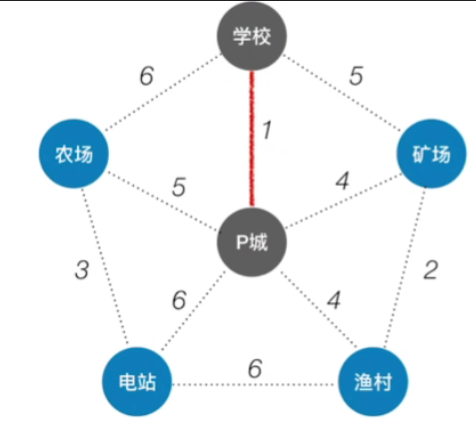
2. 接下来查看已经纳入生成树的所有顶点的边,找到代价最小的边,也就是4这两条边,也就是说我们可以把矿场先连到这个树里,也可以把渔村先连到这个树里,这里我们挑选矿场
   

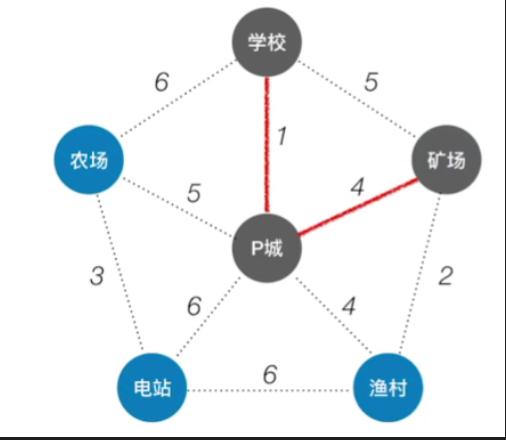
3. 接下来不用多说,只需将其余所有顶点按照之前方法纳入生成树即可,最终结果如下
   

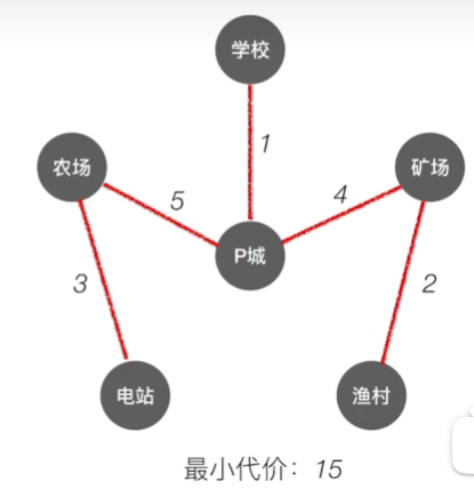
3.实现思想

1.思路

• 从V₀开始，总共需要n-1轮处理
• 每一轮处理：循环遍历所有个结点，找到lowCast最低的，且还没加入树的顶点。
• 再次循环遍历，更新还没加入的各个顶点的lowCast值

2.具体实现步骤

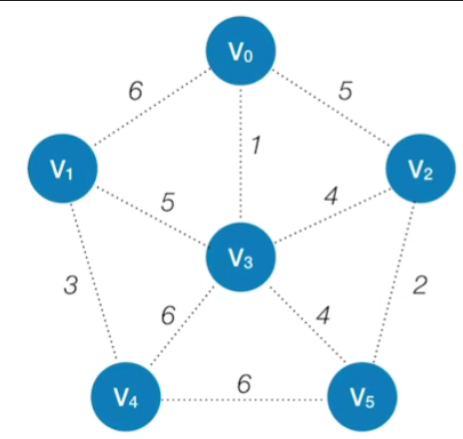
1. 定义

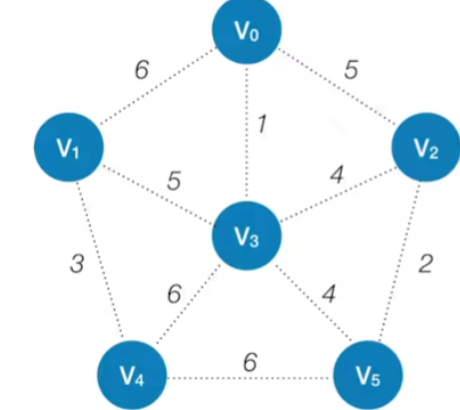
   1. 我们假设我们挑选了从V0这个顶点开始
   2. 然后我们需要这样的两个数组
      

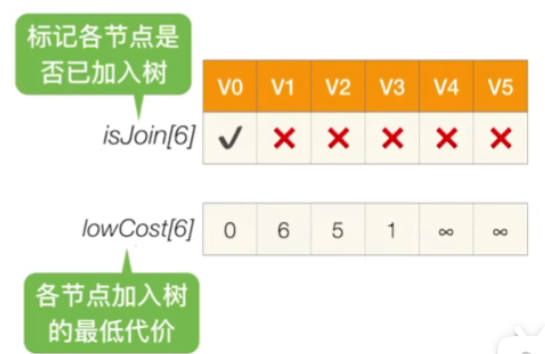
2. 初始化

   1. 现在我们只选中了V0,那么V1和V0之间是有一条边的,这条边的权值是6,所以就目前来看,接下来如果我们要把V1加入到我们已经组建的这个生成树里边,那所需要付出的最低代价应该是6这么多,所以lowCost数组里面对应V1的位置填6
   2. 那V2和V0之间也有边,所以如果把V2加入,那需要的最低代价应该是5,而V3和V0之间的边是1,所以在lowCost对应的V2,V3的位置分别填写5,1
   3. 而V4,V5这两个顶点和V0之间没有直接相连的边,因此在lowCost对应的位置填上∞
      

3. 接下来需要进行第一轮处理

   1. 第一轮处理需要检查这两个数组的值

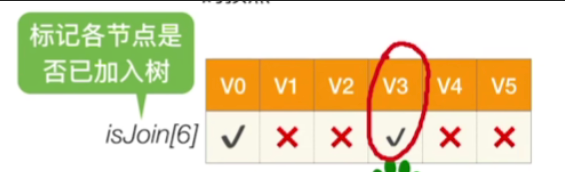
   2. 然后我们会找出一个当前还没有被加入这个生成树,同时lowCost值最低的一个顶点

   3. 那显然V3的这个lowCost代价是最小的,所以我们把V3加入到这个正在构建的生成树,同时将对应的isJoin值设为true
      

   4. 再次循环遍历,更新还没加入的各个顶点的lowCost值(在加入了V3这个顶点之后,其他的这些还没有被加入这棵树的顶点,在接下来加入这棵树的代价有可能会改变,也就是lowCost这个值会变)

   5. 检查V1和v3之间的这条边,这条边的权值5很显然是小于6的,因此如果接下来要把V1把它加到这棵树里,那所需要付出的最低代价其实就变成了5

   6. 那对于V2也是一样,如果接下来让V2和V3通过4这条边相连,那么4这个代价很显然要比之前的五这个代价要更低一些,因此如果接下来要把V2把它加到这棵树里,那所需要付出的最低代价其实就变成了4

   7. 其他顶点也是一样的操作,V4,V5对应的lowCost值分别变为6,4
      

4. 接下来重复第一轮的操作,直到所有顶点加入生成树为止

4.时间复杂度

1.推导

• 由于每一轮的循环都会选择一个新的顶点进行处理,那总共有n个顶点,就需要n-1轮的循环,而每一轮的处理当中又需要进行两次循环遍历,遍历所有的节点来处理他们的lowCost,所以每一轮的处理时间复杂度就是O(2n)这样的一个数量级,那可以舍弃常数项为O(n)
• 那总共n-1轮的循环,结果时间复杂度为(n-1)O(n),省略常数项,得到最终的时间复杂度为O(n²)

2.结论

• O(|V|²)适合用于边稠密图

2.Kruskal算法(克鲁斯卡尔)

1.方法

• 每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选),直到所有结点都连通

2.例子

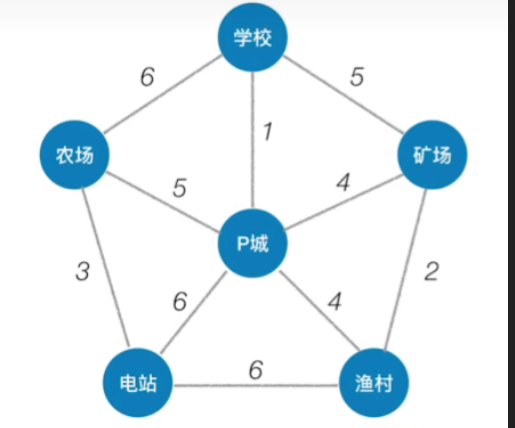
1. 现在我们要从所有的这些边里边挑出权值最小的一条,显然全值最小的应该是1这条边,那1这条边的两头也就是学校和p城这两个顶点,此时他们还没有连通,所以我们把这条边选中,这样的话两边的节点就连通了
   

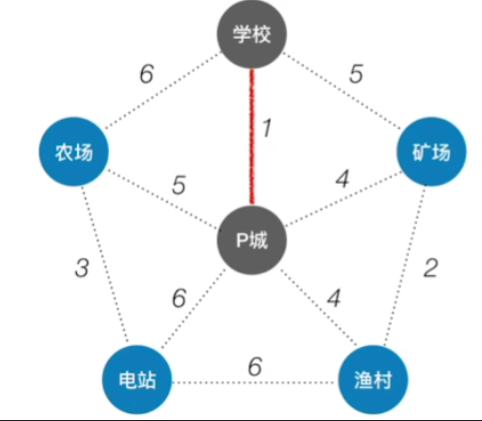
2. 接下来做的事情还是一样的,我们再从剩下的这些边当中挑选出权值最小的一条边,那显然2这条边的权值是最小的,而它两头的渔村和矿场此时还没有连通,所以我们把这条边给加上
   

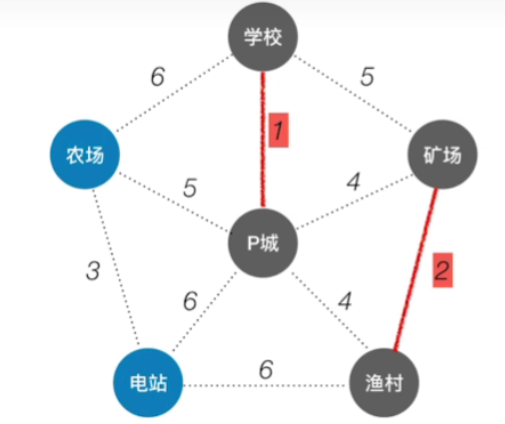
3. 再往后权值最小的一条边应该是3这条边,而这条边两头的顶点此时没有连通,所以我们把这条边给选上
   

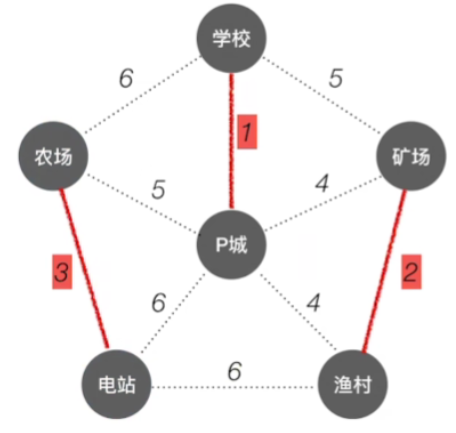
4. 接下来我们再从剩余的这些边当中挑选出权值最小的4,对于矿场和p城这两个顶点,此时还没有连通,所以我们挑上面这条边,下面那条也是一样的,任选一条就可以,这里我们选上面那一条
   

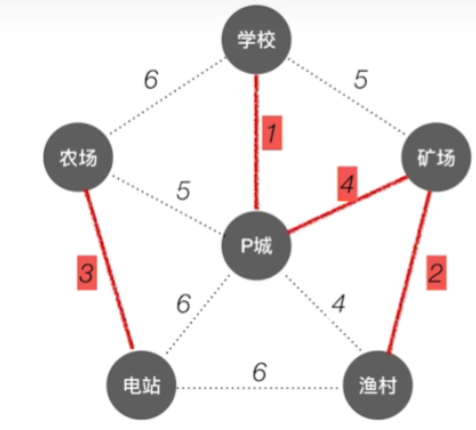
5. 接下来依然重复之前的动作,从剩余的这些边当中得知4是权值最小的,但是P城与渔村已经连通,所以无需连接.

6. 那么,接下来权值最小的应该是5,在权值为5的边中,学校与矿场已经连通,因此无需连接,剩下的农场与P城还未连通,因此选中连接农场与P城这一条边
   

3.实现方法

1.思路

• 初始化按边权值给边排序
• 并查集判断顶点是否连通,不连通则加入生成树同时归并相应集合,连通则跳过

2.实现具体步骤

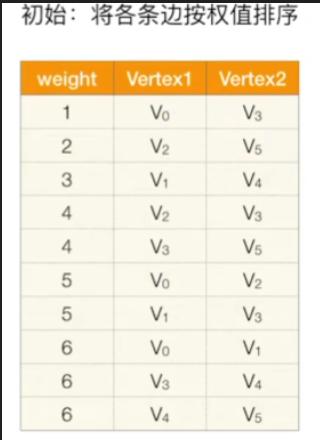
1. 预处理

   1. 先把各条边按照权值递增的次序做一个排序,那权值最小的边是1,两边连的是V0和V3,因此在表中填上1,V0,V3
   2. 其他边也是这样,最终结果如下
      

2. 第一轮处理

   1. 这个算法执行过程就是要把所有的这些边都检查一遍
   2. 那第一条边它的权值是1,两边连的顶点是V0和V3,那接下来要做的一件事情是要检查这条边的两个顶点,他们此时是否已经连通(用到了并查集)
   3. 刚开始要把所有的这些节点,把它们分别看作是不同的集合,不同集合的元素之间不连通,相同集合的元素之间是连通的,通过这一点就可以判断是否可以选择某一条边
   4. 所以对于第一条边的两个顶点V0,V3,他们刚开始是从属于不同集合的,也就意味着他们此时不连通,我们就可以把这条边给选上(假设是连通的,则跳过这条边)
   5. 同时如果把这两个顶点给连上的话,那这两个顶点就变成了同一个集合

3. 接下来重复第一轮的操作,直到表中所有的边全部处理完为止

4.时间复杂度

1.推导

• 共执行|E|轮，每轮判断两个顶点是否属于同一集合，需要O(log₂|E|)
• 相乘得到时间复杂度为O(|E|log₂|E|)

2.结论

• O(|E|log₂|E|)适合用于边稀疏图

四.知识回顾与重要考点

普利姆算法还可以优化,有兴趣可以看看《算法导论》这本书

结语

懈怠了,但是最近在调整了

如果想查看更多章节,请点击:一、数据结构专栏导航页