opencv学习笔记7：对mnist数据集分类

目录

一.概念介绍

1.mnist数据集介绍

（1）训练集（Training Set）

（2）测试集（Test Set）

二.代码讲解

1.加载mnist数据集

（1）打印图像验证

解释(60000,)的含义：

2.取mnist部分样例

3.定义sift特征提取函数

（1）空列表[]可以动态地添加元素，

（2）

（3）features.append(des.mean(axis=0))

为什么取平均值？

4.hog特征函数

4.SVM模型训练与预测

5.打印混淆矩阵

6. 找到预测错误的样本索引（取前5个）

三.总代码

1.网上历程

2.sift特征提取完整代码及结果

3.hog特征提取完整代码及结果

---

一.概念介绍

1.mnist数据集介绍

MNIST是一个经典的手写数字图像数据集，包含0-9共10类手写数字图片，是机器学习和计算机视觉领域的基础测试数据集。

（1）训练集（Training Set）

训练集是用于训练模型的数据集合。
模型通过学习训练集中样本的特征（如图像的像素值）与标签（如数字“5”）之间的对应关系，不断调整自身参数（比如SVM中的超平面参数、神经网络的权重），从而掌握“识别手写数字”的能力。
例如，MNIST训练集包含60000张手写数字图片及对应标签，模型会从这60000个样本中“学习”数字的形态特征。

（2）测试集（Test Set）

测试集是用于评估模型泛化能力的数据集合。
测试集的样本与训练集独立（即测试样本未参与模型训练），通过让模型对测试集样本进行预测，对比预测结果与真实标签，可判断模型是否真正学会了“识别规律”，而非单纯“记住”训练样本（即避免过拟合）。
例如，MNIST测试集包含10000张手写数字图片及对应标签，用于检验训练好的模型对新的、未见过的手写数字的识别准确率。

简单来说，训练集是模型的“课本”，测试集是模型的“期末考试卷”——用课本学习，用试卷检验学习效果。

二.代码讲解

核心任务：

MNIST数据集---图片提取特征(sift, hog都行)---特征进行机器学习用svm分类器---得到模型之后进行图像分类

1.加载mnist数据集

核心代码就最后一行

import matplotlib.pyplot as plt
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()

（1）打印图像验证

import matplotlib.pyplot as plt
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 查看数据集形状
print("训练集图像形状:", x_train.shape)  # 预期输出 (60000, 28, 28)
print("训练集标签形状:", y_train.shape)  # 预期输出 (60000,)
print("测试集图像形状:", x_test.shape)    # 预期输出 (10000, 28, 28)
print("测试集标签形状:", y_test.shape)    # 预期输出 (10000,)plt.imshow(x_train[0], cmap='gray')
plt.title(f"标签：{y_train[0]}")
plt.axis('off')
plt.show()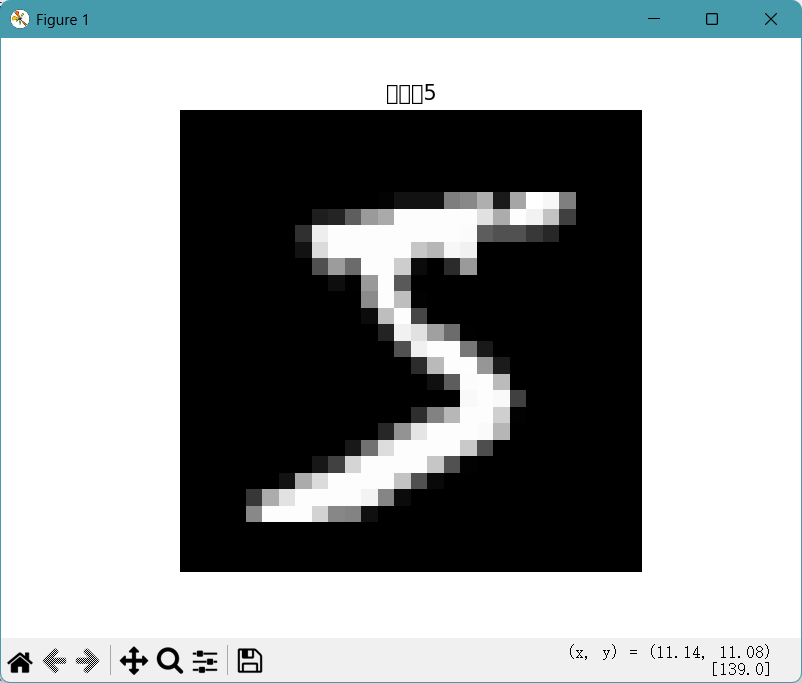

1. import matplotlib.pyplot as plt导入matplotlib库的pyplot模块，并简写为plt。matplotlib是 Python 中常用的绘图库，pyplot模块提供了类似 MATLAB 的绘图接口，用于后续显示图像。

2. from keras.datasets import mnist从 Keras（深度学习框架）的数据集模块中导入mnist数据集。MNIST 是一个经典的手写数字数据集，包含 0-9 的手写数字图片及对应的标签，常用于机器学习入门案例。

3. (x_train, y_train), (x_test, y_test) = mnist.load_data()加载 MNIST 数据集，并按训练集和测试集拆分：

   • x_train：训练集图像数据（用于模型训练）存着6000张28×28的图片
   • y_train：训练集标签（图像对应的数字，0-9）存着6000张图片的数字标签，表示他是数字几
   • x_test：测试集图像数据（用于模型评估）
   • y_test：测试集标签（测试图像对应的数字）

4. print("训练集图像形状:", x_train.shape)打印训练集图像的形状。shape是 NumPy 数组的属性，表示数组的维度。MNIST 训练集包含 60000 张图片，每张图片是 28×28 像素的灰度图，因此输出为 (60000, 28, 28)。

5. print("训练集标签形状:", y_train.shape)打印训练集标签的形状。每个图像对应一个标签（0-9），因此 60000 个标签构成一维数组，输出为 (60000,)。

6. print("测试集图像形状:", x_test.shape)打印测试集图像的形状。MNIST 测试集包含 10000 张 28×28 的灰度图，输出为 (10000, 28, 28)。

   • 解释(60000,)的含义：

   • 在 Python 的 NumPy 数组中，(60000,) 表示这是一个一维数组，数组的长度是 60000。
   • 对于多维数组，形状会用多个数字表示维度大小，比如(60000, 28, 28)表示三维数组，第一个维度长度 60000，第二个 28，第三个 28。
   • 而一维数组的形状只需要一个数字来表示长度，但为了保持和多维数组形状表示的一致性（区分单个数字和标量），会在数字后面加一个逗号，所以写成(60000,)。这里的逗号不是表示有第二个维度，而是用来明确这是一个数组的形状（一维），而非一个单独的数字。

7. print("测试集标签形状:", y_test.shape)打印测试集标签的形状。10000 个标签构成一维数组，输出为 (10000,)。

8. plt.imshow(x_train[0], cmap='gray')显示训练集中的第一张图像（x_train[0]）。imshow是pyplot的图像显示函数，cmap='gray'指定用灰度配色方案（符合 MNIST 灰度图的特性）。

9. plt.title(f"标签：{y_train[0]}")为图像添加标题，显示该图像对应的标签（y_train[0]，即第一张图像的数字）。这里使用 f-string 格式化字符串，动态插入标签值。

10. plt.axis('off')关闭图像的坐标轴显示（去除 x 轴和 y 轴的刻度，使图像更简洁）。

11. plt.show()显示绘制的图像窗口，执行后会弹出一个窗口展示第一张 MNIST 图像及对应标签。

2.取mnist部分样例

取mnist训练集的前10000个样本、测试集的前2000个样本，加快代码运算，没什么好说的

# 为加速计算，取部分数据（全量数据训练较慢）
n_train, n_test = 10000, 2000  # 训练集取10000样本，测试集取2000样本
x_train_sub = x_train[:n_train]  # 取前10000张训练图像
y_train_sub = y_train[:n_train]  # 对应前10000个训练标签
x_test_sub = x_test[:n_test]     # 取前2000张测试图像
y_test_sub = y_test[:n_test]     # 对应前2000个测试标签

3.定义sift特征提取函数

（1）空列表[]可以动态地添加元素，

• 后面for循环我们遍历每一张图像（for img in images），对每张图像提取 SIFT 特征后，将其特征（通过des.mean(axis=0)计算得到的均值）逐个添加到features列表中。
• 列表的长度会随着图像数量的增加而动态扩展，因此可以存储所有图像的特征。

def extract_sift_features(images):"""提取SIFT特征（取描述子均值作为图像特征）"""sift = cv2.SIFT_create()  # 初始化SIFT特征检测器features = []  # 创建一个空列表features，用于存储每张图像提取后的特征向量for img in images:  # 遍历每张图像# 检测关键点（kp）和计算描述子（des）kp, des = sift.detectAndCompute(img, None)# 若无关键点（des为None），用0矩阵填充（避免维度不一致）if des is None:des = np.zeros((1, 128))  # SIFT描述子固定为128维# 取所有描述子的平均值作为图像特征（统一特征长度）features.append(des.mean(axis=0))return np.array(features)  # 转为numpy数组返回

（2）

1. kp, des = sift.detectAndCompute(img, None)对当前图像img执行 SIFT 特征提取：

   • sift.detectAndCompute()是核心方法，第一个参数是输入图像（通常为灰度图），第二个参数是掩码（None表示不使用掩码，处理整幅图像）。
   • 返回值kp是图像中检测到的关键点（KeyPoint 对象列表，包含位置、尺度等信息）。
   • 返回值des是关键点对应的描述子（一个二维数组，形状为(N, 128)，其中N是关键点数量，128 是每个描述子的固定维度）。

2. if des is None:判断描述子des是否为None。极端情况下（如图像全黑），可能检测不到任何关键点，此时des会为None。

3. des = np.zeros((1, 128)) # SIFT描述子固定为128维若des为None，则用一个(1, 128)的零矩阵填充。这是为了避免后续计算均值时出现错误，同时保证特征维度统一（始终为 128 维）。

（3）features.append(des.mean(axis=0))

• des：是 SIFT 特征的描述子，它是一个二维 NumPy 数组，形状通常为(关键点数, 128)（因为 SIFT 描述子是 128 维的）。
• des.mean(axis=0)：
  • mean是 NumPy 的均值计算方法。
  • axis=0表示沿着 “列” 的方向计算均值（即对每一个维度（共 128 维），计算所有关键点在该维度上的平均值）。最终会得到一个形状为(128,)的一维数组，它代表了这张图像所有 SIFT 关键点描述子的 “均值特征”。

  • (128,)解释：举例来说，如果你用 np.array([1,2,3,4]) 创建数组，它的形状就是 (4,)—— 表示这是一个一维数组，包含 4 个元素。(128,)表示它是一个128长度的一维数组

  • 回到 SIFT 特征的场景中，des.mean(axis=0) 的结果是 (128,) 形状的数组，意味着它是一个128 维的特征向量，每个元素对应 SIFT 描述子中某一维度的平均值。

• features.append(...)：将这张图像的 “均值特征” 添加到features列表中，以便后续存储所有图像的特征。

为什么取平均值？

有n个关键点的描述子，对128维描述子的每一个维度上的n个数据取平均值，把这一维上的n个数据取平均值变成了1个数据。取平均值的核心目的确实是将图像中多个局部关键点的描述子（一共n个关键点，每个关键点对应一个 128 维向量）聚合为整张图像的全局描述子（一个 128 维向量），好处是节省空间、减少计算量等。

简单来说，这行代码的作用是：对当前图像的所有 SIFT 描述子按维度求均值，得到一个 128 维的 “平均特征”，并将这个特征添加到features列表中。

4.hog特征函数

def extract_hog_features(images):"""提取HOG特征（方向梯度直方图）"""# HOG参数配置（根据MNIST图像尺寸28×28设计）winSize = (28, 28)  # 窗口大小（必须与输入图像尺寸一致）blockSize = (14, 14)  # 块大小（由细胞单元组成，需能被winSize整除）blockStride = (7, 7)  # 块滑动步长（每次移动的像素数，需为cellSize的整数倍）cellSize = (7, 7)  # 细胞单元大小（每个细胞的像素尺寸）nbins = 9  # 梯度方向的直方图 bins 数量（0-180度，每20度一个bin）# 初始化HOG特征提取器hog = cv2.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins)features = []  # 存储所有图像的特征for img in images:  # 遍历每张图像# HOG函数要求输入为3通道图像，将灰度图转为BGR格式（3通道）img_3d = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)# 计算HOG特征并展平为一维向量hog_feature = hog.compute(img_3d).flatten()features.append(hog_feature)return np.array(features)  # 转为numpy数组返回

• cv2.cvtColor(...)：将单通道灰度图（img，形状为 (28,28)）转换为 3 通道 BGR 图（img_3d，形状为 (28,28,3)）。
• 原因：OpenCV 的 hog.compute() 函数默认要求输入图像为 3 通道（即使三个通道内容相同），否则可能报错，因此需要这一步转换。
• hog.compute(img_3d) 返回一个二维数组 (N, 1)，而flatten让它变成一维数组
  • N 是 HOG 特征的总数量（例如 144，由前面的参数计算得出），表示有 N 个特征值。
  • 1 表示这些特征值被组织成1 列，每个特征值单独占一行。
  • 

4.SVM模型训练与预测

# 4. SVM模型训练与预测
svm = SVC(kernel='rbf', gamma='scale')  # 径向基核SVM
svm.fit(x_train_feat, y_train_sub)       # 训练模型
y_pred = svm.predict(x_test_feat)        # 测试预测

①这个svm实例是一个基于 RBF 核、自动缩放gamma的支持向量机分类器，它通过核函数将数据映射到高维空间，再通过支持向量和最优超平面对样本进行分类

②训练模型

③测试预测：对2000个测试数据分类，看看这些图片是0~9哪个数字。

• y_pred 的长度与测试集样本数量一致。例如，若 x_test_feat 包含 2000 张测试图像，y_pred 就有 2000 个元素。
• 每个元素对应测试集中一张图像的预测类别（与训练时的标签格式一致）。

在 MNIST 手写数字分类任务中，训练时的标签 y_train_sub 是 0-9 的整数（分别代表数字 0 到 9）。因此：y_pred 中的每个元素也是 0-9 之间的整数，表示模型判断该测试图像对应的手写数字是几。

例如：

• 若 y_pred[0] = 5，表示模型预测测试集中第 1 张图像是数字 “5”；
• 若 y_pred[100] = 3，表示模型预测测试集中第 101 张图像是数字 “3”。

5.打印混淆矩阵

混淆矩阵直观展示哪些数字容易被混淆（如 4 和 9、3 和 5，因形状相似）

• confusion_matrix(y_test_sub, y_pred)：传入测试集标签和分类后的标签，返回(10,10)的矩阵，cm[i][j]表示真实标签为i的样本被预测为j的数量。

cm = confusion_matrix(y_test_sub, y_pred)  # 计算混淆矩阵
plt.figure(figsize=(8, 6))  
# 创建8×6英寸的图像，figure用于创建一个图像窗口，所有的绘图元素都会绘制在这个窗口上。
plt.imshow(cm, cmap='Blues')  # 用蓝色渐变显示矩阵值（值越大越蓝）
plt.title(f"混淆矩阵 (准确率: {acc:.4f})")  # 标题包含准确率
plt.colorbar()  # 添加颜色条（指示数值与颜色的对应关系）
plt.xticks(range(10)), plt.yticks(range(10))  # 坐标轴刻度为0-9（数字标签）
plt.xlabel('预测标签'), plt.ylabel('真实标签')  # 坐标轴名称
plt.show()  # 显示图像

6. 找到预测错误的样本索引（取前5个）

• y_pred != y_test_sub：逐元素比较 “预测标签” 和 “真实标签”，返回一个布尔数组（True表示预测错误，False表示正确）。
  • np.where(...)：根据布尔数组返回 “True所在的位置索引”，结果是一个元组（格式为(array([索引1, 索引2, ...]),)）。

    (array([5, 10, 15]),)    #元组里面包含一个数组

• [0]：取元组中的第一个元素（即错误样本的索引数组）。例如上面这个元组就是取出array([5, 10, 15])这个数组
• [:5]：截取前 5 个索引（只看前 5 个错误样本）。取出数组中前五个元素

• errors：是一个存储 “错误样本索引” 的数组（比如 [10, 25, 33, 47, 52]，表示测试集中这 5 个位置的样本预测错误）。

• enumerate(errors)：对 errors 进行遍历，每次循环会返回两个值：
  1. 循环计数（从 0 开始）：即当前元素在 errors 中的索引（比如第 1 次循环是 0，第 2 次是 1，直到 4）。
  2. errors 中的元素值：即具体的错误样本索引（比如 10、25 等）。

# 找到预测错误的样本索引（取前5个）
errors = np.where(y_pred != y_test_sub)[0][:5]
plt.figure(figsize=(10, 2))  # 创建10×2英寸的图像
for i, idx in enumerate(errors):  # 遍历错误样本索引plt.subplot(1, 5, i+1)  # 1行5列的子图，第i+1个位置plt.imshow(x_test_sub[idx], cmap='gray')  # 显示原始图像（灰度图）# 标题显示真实标签和预测标签plt.title(f"真: {y_test_sub[idx]}\n预: {y_pred[idx]}")plt.axis('off')  # 关闭坐标轴（减少干扰）
plt.show()  # 显示图像

三.总代码

1.网上历程

import numpy as np
import matplotlib.pyplot as plt
import cv2
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, confusion_matrix
from tensorflow.keras.datasets import mnist# 1. 数据加载与预处理
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype(np.uint8)  # 转为OpenCV兼容的uint8类型
x_test = x_test.astype(np.uint8)# 为加速计算，取部分数据（全量数据训练较慢）
n_train, n_test = 10000, 2000
x_train_sub = x_train[:n_train]
y_train_sub = y_train[:n_train]
x_test_sub = x_test[:n_test]
y_test_sub = y_test[:n_test]# 2. 特征提取函数定义
def extract_sift_features(images):"""提取SIFT特征（取描述子均值作为图像特征）"""sift = cv2.SIFT_create()features = []for img in images:kp, des = sift.detectAndCompute(img, None)  # 检测关键点和描述子if des is None:  # 无关键点时用0填充des = np.zeros((1, 128))features.append(des.mean(axis=0))  # 平均描述子作为特征return np.array(features)def extract_hog_features(images):"""提取HOG特征（方向梯度直方图）"""# HOG参数配置winSize = (28, 28)        # 检测窗口大小blockSize = (14, 14)      # 块大小（2x2细胞）blockStride = (7, 7)      # 块步长（1个细胞）cellSize = (7, 7)         # 细胞大小nbins = 9                 # 方向直方图的区间数hog = cv2.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins)features = []for img in images:img_3d = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)  # 转为3通道（HOG函数要求）hog_feature = hog.compute(img_3d).flatten()  # 计算并展平特征features.append(hog_feature)return np.array(features)# 3. 提取特征（二选一或全跑，HOG效果更好）
# x_train_feat = extract_sift_features(x_train_sub)
# x_test_feat = extract_sift_features(x_test_sub)
x_train_feat = extract_hog_features(x_train_sub)
x_test_feat = extract_hog_features(x_test_sub)# 4. SVM模型训练与预测
svm = SVC(kernel='rbf', gamma='scale')  # 径向基核SVM
svm.fit(x_train_feat, y_train_sub)       # 训练模型
y_pred = svm.predict(x_test_feat)        # 测试预测# 5. 结果评估与可视化
# 计算准确率
acc = accuracy_score(y_test_sub, y_pred)
print(f"分类准确率: {acc:.4f}")# 混淆矩阵可视化
cm = confusion_matrix(y_test_sub, y_pred)
plt.figure(figsize=(8, 6))
plt.imshow(cm, cmap='Blues')
plt.title(f"混淆矩阵 (准确率: {acc:.4f})")
plt.colorbar()
plt.xticks(range(10)), plt.yticks(range(10))
plt.xlabel('预测标签'), plt.ylabel('真实标签')
plt.show()# 错误案例展示
errors = np.where(y_pred != y_test_sub)[0][:5]  # 取前5个错误样本
plt.figure(figsize=(10, 2))
for i, idx in enumerate(errors):plt.subplot(1, 5, i+1)plt.imshow(x_test_sub[idx], cmap='gray')plt.title(f"真: {y_test_sub[idx]}\n预: {y_pred[idx]}")plt.axis('off')
plt.show()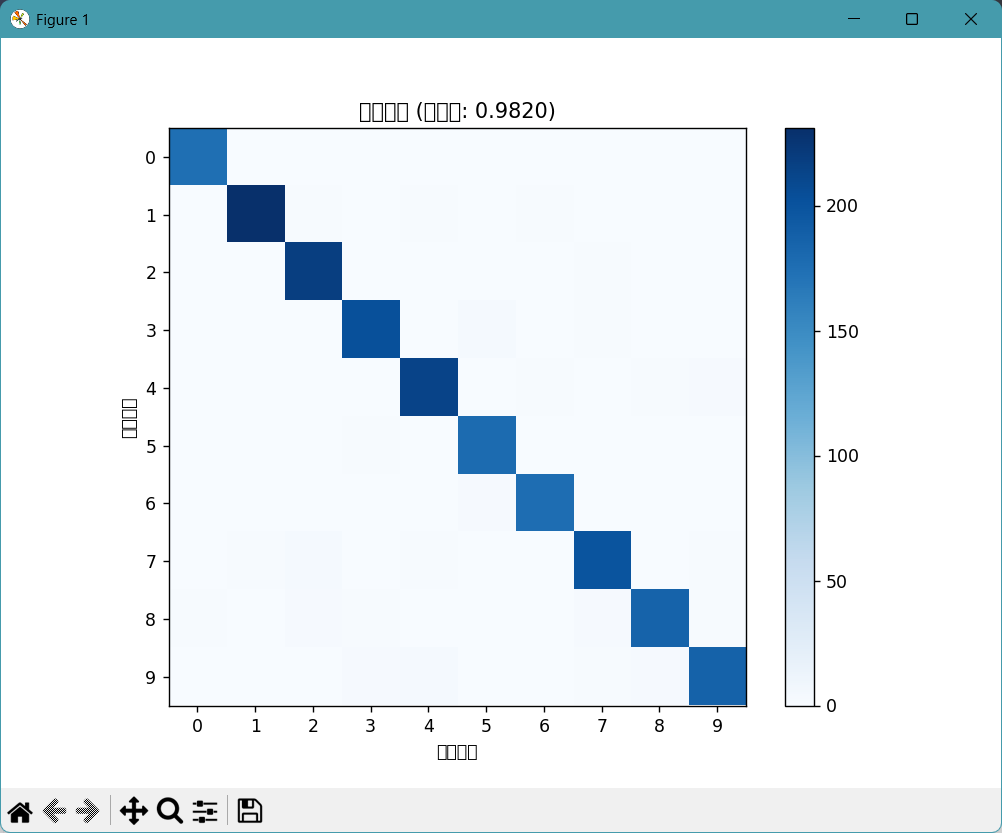

2.sift特征提取完整代码及结果

import cv2
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from keras.datasets import mnist
from sklearn.metrics import accuracy_score,confusion_matrix(x_train,y_train),(x_test,y_test)=mnist.load_data()
x_train=x_train.astype(np.uint8)
x_test=x_test.astype(np.uint8)n_train,n_test=10000,2000
x_train_sub=x_train[:n_train]
y_train_sub=y_train[:n_train]
x_test_sub=x_test[:n_test]
y_test_sub=y_test[:n_test]#特征提取
def extract_sift_features(images):sift=cv2.SIFT_create()features=[]for img in images:kp,des=sift.detectAndCompute(img,None)if des is None:des=np.zeros((1,128))features.append(des.mean(axis=0))return np.array(features)x_train_feat=extract_sift_features(x_train_sub)
x_test_feat=extract_sift_features(x_test_sub)
#svm分类
svm=SVC(kernel='rbf',gamma='scale')
svm.fit(x_train_feat,y_train_sub)
y_pred=svm.predict(x_test_feat)#结果评估
acc=accuracy_score(y_test_sub,y_pred)
print(f"分类准确率：{acc:.4f}")
#混淆矩阵
cm=confusion_matrix(y_test_sub,y_pred)
plt.figure(figsize=(8,6))
plt.imshow(cm,cmap='Blues')
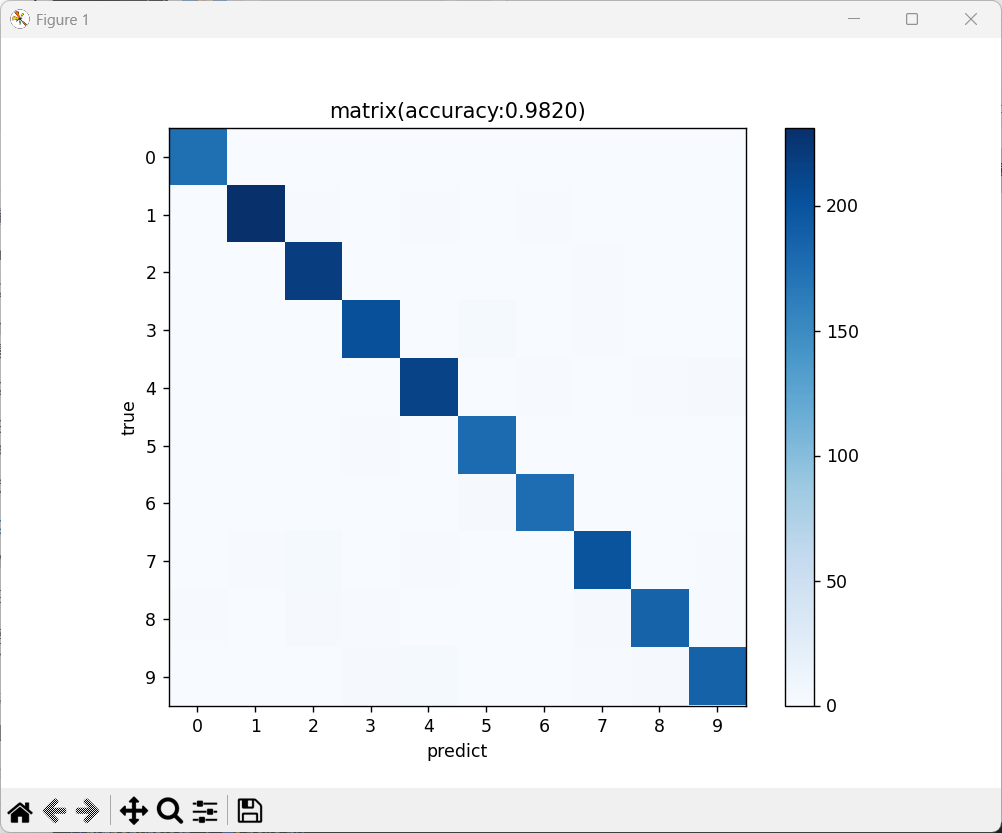
plt.title(f"matrix(accuracy:{acc:.4f})")
plt.colorbar()
plt.xticks(range(10)),plt.yticks(range(10))
plt.xlabel('predict'),plt.ylabel('true')
plt.show()#错误案例展示
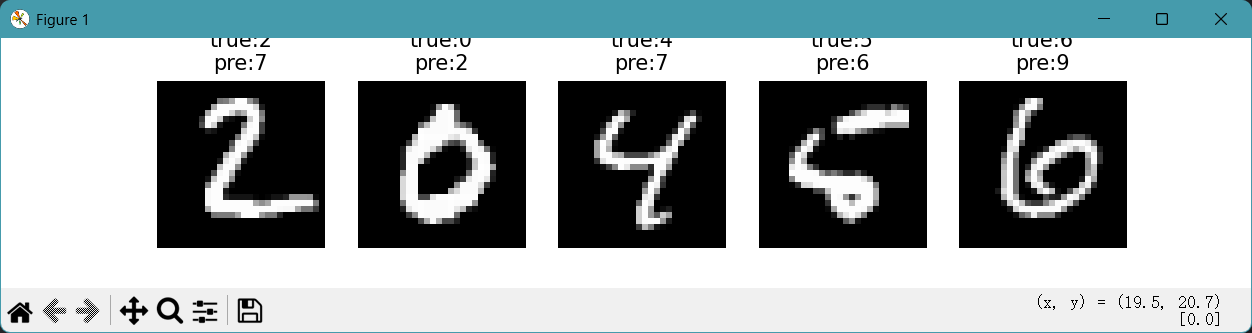
errors=np.where(y_pred!=y_test_sub)[0][:5]
plt.figure(figsize=(10,2))
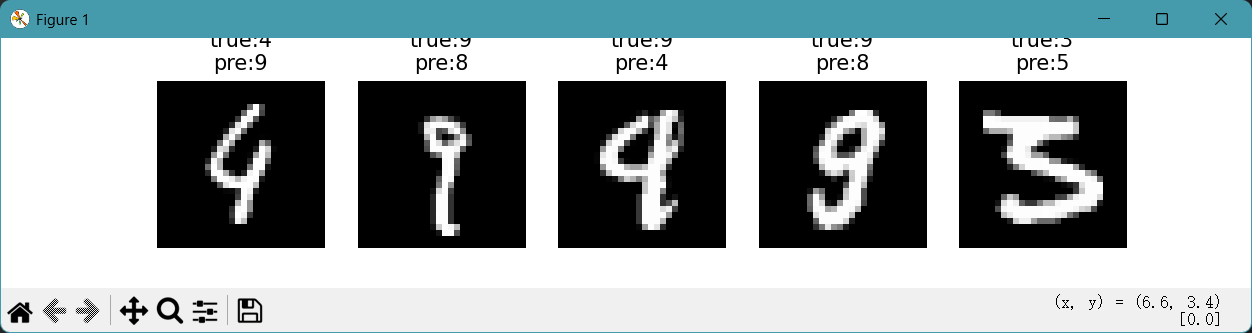
for i,idx in enumerate(errors):plt.subplot(1,5,i+1)plt.imshow(x_test_sub[idx],cmap='gray')plt.title(f"true:{y_test_sub[idx]}\npre:{y_pred[idx]}")plt.axis('off')
plt.show()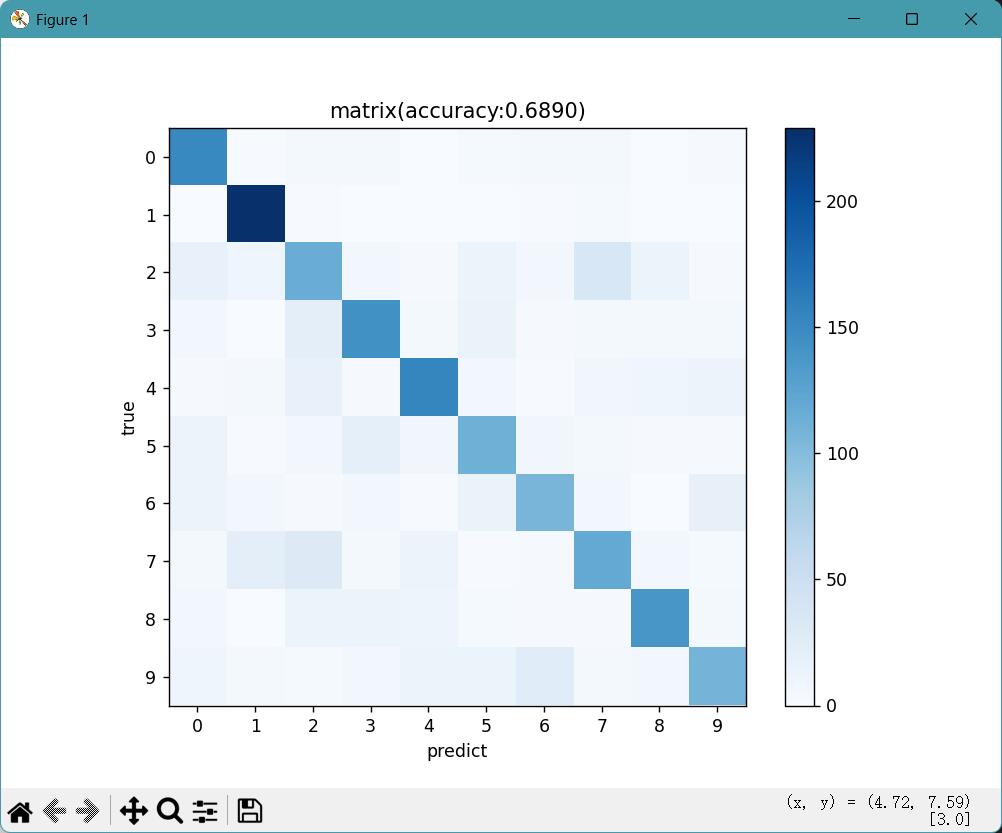

3.hog特征提取完整代码及结果

import cv2
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from keras.datasets import mnist
from sklearn.metrics import accuracy_score,confusion_matrix(x_train,y_train),(x_test,y_test)=mnist.load_data()
x_train=x_train.astype(np.uint8)
x_test=x_test.astype(np.uint8)n_train,n_test=10000,2000
x_train_sub=x_train[:n_train]
y_train_sub=y_train[:n_train]
x_test_sub=x_test[:n_test]
y_test_sub=y_test[:n_test]def extract_hog_features(images):winSize=(28,28)blockSize=(14,14)blockStride=(7,7)cellSize=(7,7)nbins=9hog=cv2.HOGDescriptor(winSize,blockSize,blockStride,cellSize,nbins)features=[]for img in images:img_3d=cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)hog_feature=hog.compute(img).flatten()features.append(hog_feature)return np.array(features)
# x_train_feat=extract_sift_features(x_train_sub)
# x_test_feat=extract_sift_features(x_test_sub)
x_train_feat=extract_hog_features(x_train_sub)
x_test_feat=extract_hog_features(x_test_sub)
#svm分类
svm=SVC(kernel='rbf',gamma='scale')
svm.fit(x_train_feat,y_train_sub)
y_pred=svm.predict(x_test_feat)#结果评估
acc=accuracy_score(y_test_sub,y_pred)
print(f"分类准确率：{acc:.4f}")
#混淆矩阵
cm=confusion_matrix(y_test_sub,y_pred)
plt.figure(figsize=(8,6))
plt.imshow(cm,cmap='Blues')
plt.title(f"matrix(accuracy:{acc:.4f})")
plt.colorbar()
plt.xticks(range(10)),plt.yticks(range(10))
plt.xlabel('predict'),plt.ylabel('true')
plt.show()#错误案例展示
errors=np.where(y_pred!=y_test_sub)[0][:5]
plt.figure(figsize=(10,2))
for i,idx in enumerate(errors):plt.subplot(1,5,i+1)plt.imshow(x_test_sub[idx],cmap='gray')plt.title(f"true:{y_test_sub[idx]}\npre:{y_pred[idx]}")plt.axis('off')
plt.show()